Расчет элементов коэффициента

17,44	22,95	3,00	15,77	304,15	248,56	274,96
17,28	24,84	1,56	16,35	298,60	267,36	282,55
17,92	29,97	2,88	20,14	321,13	405,72	360,95
18,88	28,08	2,28	18,70	356,45	349,61	353,01
17,12	24,30	1,20	15,86	293,09	251,50	271,50
21,12	32,40	2,64	21,57	446,05	465,43	455,64
20,00	29,97	3,48	20,40	400,00	415,97	407,91
20,64	33,48	2,28	22,10	426,01	488,56	456,21
19,68	29,70	2,52	19,82	387,30	392,86	390,07
18,40	26,73	2,40	17,90	338,56	320,30	329,30
188,48	282,42	24,24	188,61	3571,35	3605,87	3582,11

В соответствии с формулой (3.4.3) множественный коэффициент корреляции равен

.

В нашем случае . То есть 99,95% дисперсии показателяможно объяснить с помощью построенной модели зависимости оти. Рассчитанный коэффициент указывает на высокую степень соответствия математической модели фактическим данным.

Для нахождения доверительного интервала для множественного коэффициента корреляции найдем по таблицам Стьюдента (приложение Д) находим критическую точку, поэтому

.

Тогда доверительный интервал, найденный по формуле (3.4.4), имеет вид

или.

Поскольку коэффициент множественной корреляции должен находиться в границах от 0 до 1, то доверительным интервалом для него будет ,

что указывает на удачный подбор модели.

Для проверки значимости уравнения регрессиирассчитаемстатистику по формуле (3.4.5).

По таблицам Фишера (приложение Е) найдем критическое значение . Поскольку, то уравнение множественной регрессии (3.4.1) следует считают надежным.

Вычислим прогноз для и. Тогда по формуле (3.4.8) следует ожидать, что значение показателя будет равно

.

3.4.2. Матричный подход

Построение модели линейной регрессии возможно проводить матричным методом. При этом результаты наблюдений , значения объясняющих переменных, параметрыфункции регрессии записываем в виде матриц:

,,.

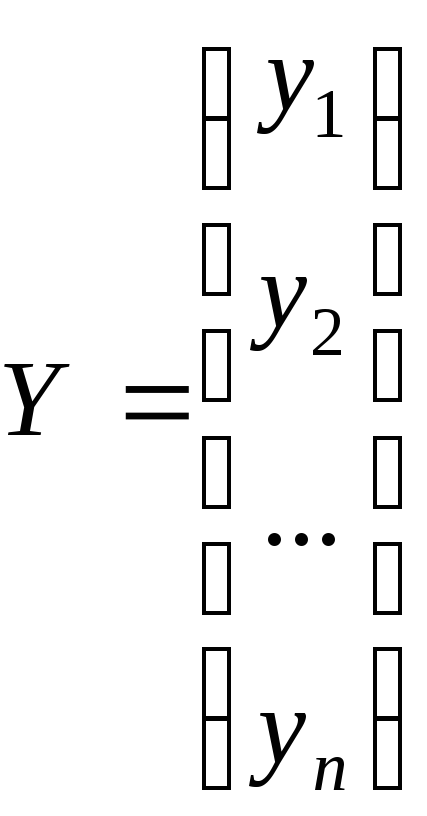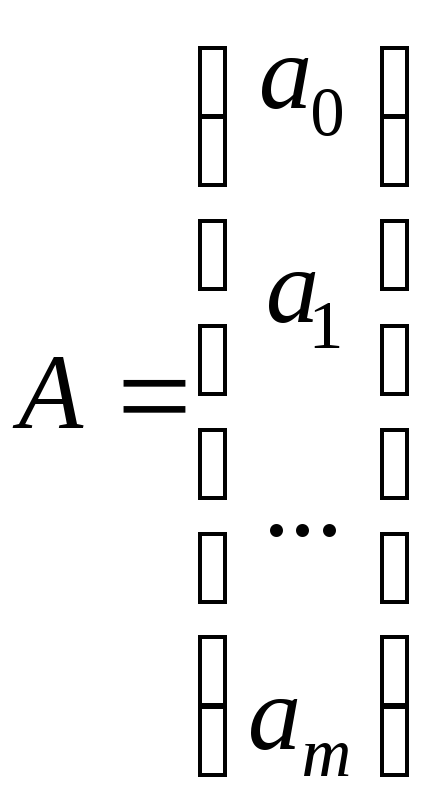При этом вводят переменные:

- вектор-столбец наблюдений над результативным показателем;

- матрица данных, причем первый столбец всегда состоит из единиц;

А - вектор-столбец коэффициентов регрессии.

Тогда уравнение регрессии в матричной форме имеет вид:

. (3.4.9)

Используя МНК, получим в качестве решения системы нормальных уравнений вектор-столбец искомых параметров регрессии:

, (3.4.10)

где - транспонированная матрица.

Таким образом, можем установить последовательность выполняемых действий:

• составить матрицу ;

• выписать вектор ;

• получить транспонированную матрицу ;

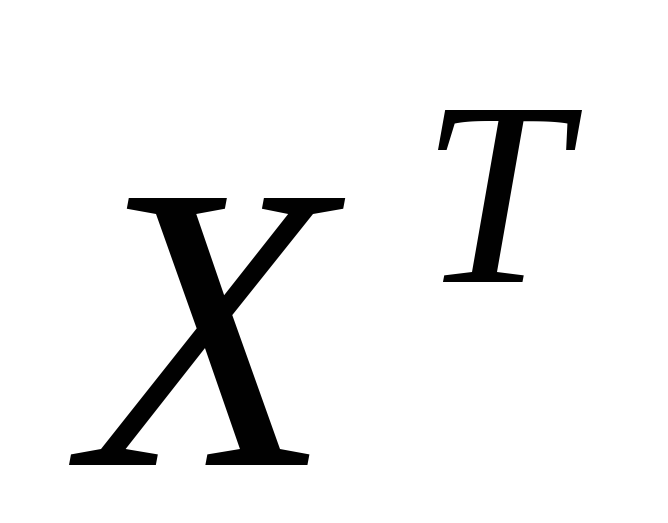• найти произведение матриц ;

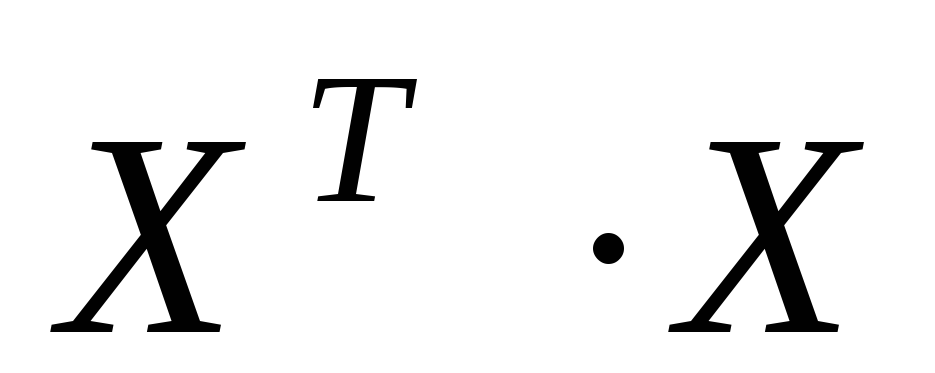• найти произведение матрицы 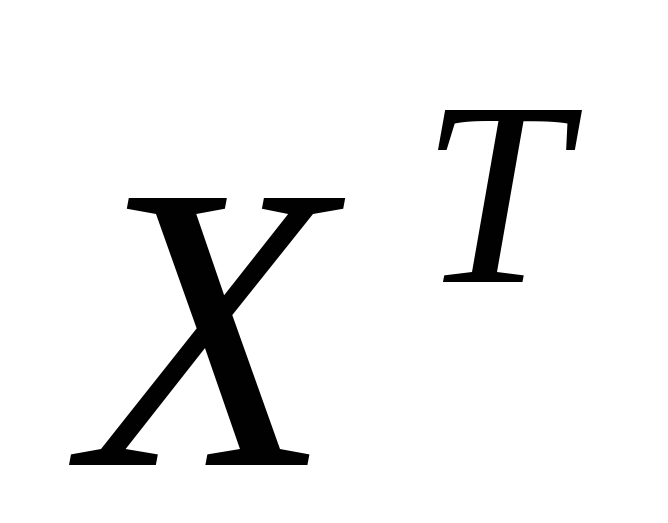на вектор;

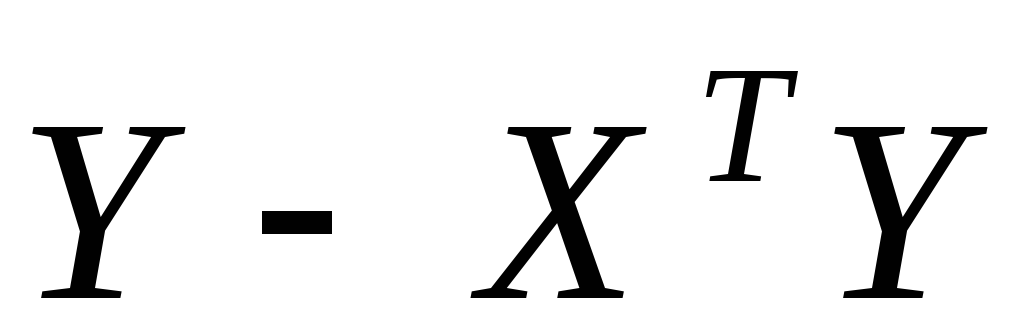• определить обратную матрицу ;

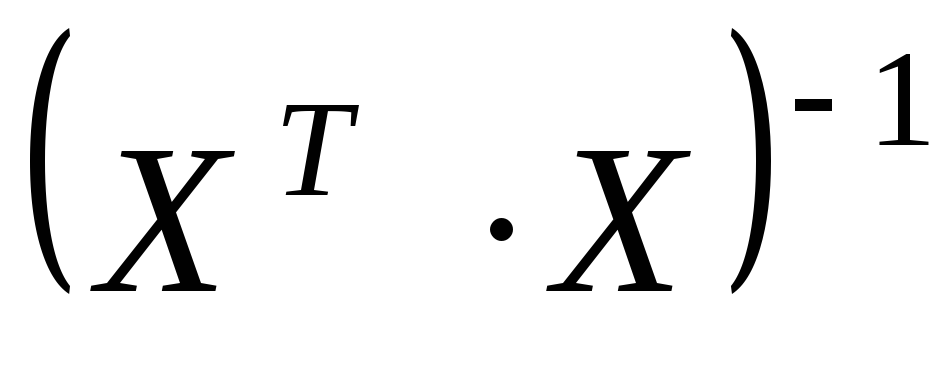• составить произведение 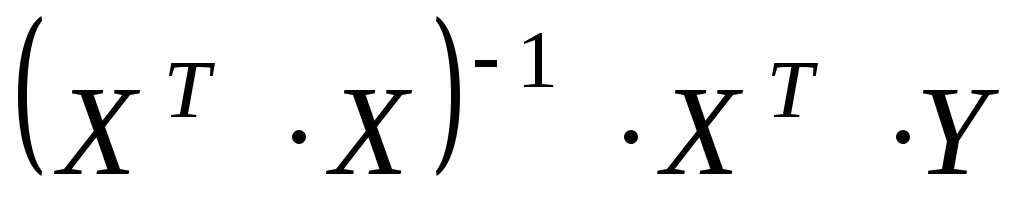, провести вычисления и определить вектор коэффициентов уравнения;

• записать моделирующее уравнение.

Переход к матричной форме позволяет, во-первых, представить алгоритм нахождения коэффициентов уравнения в более компактном конкретном виде, а во-вторых, использовать по этому алгоритму любой пакет программ, позволяющий проводить действия с матрицами.

Покажем на конкретном примере, как проводятся вычисления и находятся параметры линейного уравнения множественной регрессии.

Пример 3.9. Построить модель, которая характеризует зависимость между показателем , факторамии. Провести анализ взаимосвязи на основе полученной модели.

	2,72	3,04	2,84	2,89	2,58	2,64	2,52	2,75	2,63
	15,6	13,5	15,3	14,9	15,1	16,1	16,7	15,4	17,1
	106,3	128,5	118	121,2	120	118,4	108,4	110	105,9

Решение. Оценим параметры модели по МНК. Выпишем основные матрицы, входящие в исследование:

,

Замечание.

В матрице всегда первый столбец состоит из единиц – это связано с присутствием в уравнении свободного члена.

,

Найдем обратную матрицу:

Определим оценки параметров модели по формуле (3.4.11):

Таким образом, и искомая модель имеет вид:

.

Оценка коэффициентов уравнения

Оценку значимости коэффициентов уравнения также можно проводить на основе матричного подхода. Для этого вначале определяют дисперсии оценок параметров: ,,…,. Эти величины будут диагональными элементами матрицы:. После этого устанавливают-статистики по коэффициентам:

,,…,………………….(3.4.11)

Для рассматриваемого примера 3.9 матрица известна. Если ее диагональные элементы умножить на= 0,011851, найденное по формуле (3.1.21) то получим такие результаты:

= 3,4739,= 1, 86385;

= 0,00397,= 0, 063021;

= 0,000072,= 0, 008485.

t – статистики Стьюдента, устанавливающие значимость коэффициентов регрессионного уравнения, определяются по формулам (3.4.11), и для рассматриваемого примера таковы:

;

;

.

Зададим уровень значимости , тогда

.

Сравнивая значения t-статистик, можно сделать вывод, что коэффициент является незначимыми.

При уровне значимости имеем, поэтому коэффициентыинезначимы в построенном уравнении регресси.

3.4.3. Построение множественной регрессионной модели с использованием EXCEL

Уравнение линейной регрессии можно построить в пакете электронных таблиц Excel .

В состав пакета Excel входит набор способов анализа данных, который называется Пакетом анализа и предназначен для решения различных заданий. Для ознакомления с этим пакетом, следует в меню окна Excel выбрать опцию Сервис и в появившемся меню нужно выбрать опцию Анализ данных. В результате получим окно (рисунок 3.2).

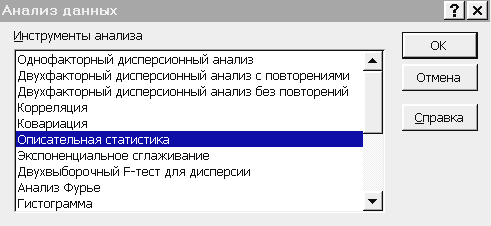
Рисунок 3.2 – Окно Анализ данных

С помощью клавиш прокрутки можно выбрать любую из приведенных функций анализа.