Алгоритм принципа максимина (минимакса)

1.В каждой строке платежной матрицы, соответствующей определенной стратегииА_іигрока А, находят минимальное из чисел:

. (2.5.1)

Это гарантированный выигрыш игрока А, при использовании стратегии А_і. Очевидно, что игроку А выгодно выбирать такую стратегиюА_і, для которой значение гарантированного выигрыша было бы самым большим.

2.Определяют число, которое находится по формуле (2.5.2)

=. (2.5.2)

Оно называется нижней ценой игрыилимаксимином. Соответствующая стратегия называется максиминной.

Максимин – это гарантированный выигрыш, который игрок А может себе обеспечить в игре против разумного противника.

Максиминная стратегия неустойчива. Если игрок А будет придерживаться максиминной стратегии, и игрок В догадается об этом, то игрок В может ухудшить положение игрока А.

3.В столбцах платежной матрицы, которые соответствует стратегиямВ_j, находят максимальное из чисел:

. (2.5.3)

Это самое худшее, что ожидает игрока В при использовании стратегий В_j– самый большой из проигрышей. Очевидно, что игрок В старается уменьшить свой проигрыш, то есть он должен выбрать стратегию, которая дает самый маленький проигрыш.

4.Определяют число, которое находится по формуле (2.5.4)

. (2.5.4)

Оно называется верхней ценой игрыилиминимаксом. Соответствующая стратегия называется минимаксной.

Минимакс – это гарантированный проигрыш, который игрок В может себе позволить в игре против разумного противника.

Минимаксная стратегия также неустойчива

Принципминимакса – это принцип осторожности, который рекомендует игрокам соблюдение максиминной и минимаксной стратегий. Он вытекает из предположения об осторожности игроков, то есть из желания разрешить конфликтную ситуацию самым лучшим образом для всех участников.

Замечание.		Нижняя цена игры всегда не превосходит верхнюю цену игры.
	Цена игры– это объективно возможный средний результат, характеризующий игру.
	Если , то выигрыш А является определенным числом, а такая игра называетсяопределенной игрой в чистых стратегияхилиигрой с седловой точкой. Выигрыш называетсязначением игры, равен элементу. Элемент является одновременно минимальным в строке, максимальным в столбцеи называетсяседловой точкой. Седловой точке отвечают оптимальные стратегии, совокупность которых является решением игры.
Замечание.		Если один из игроков придерживается своей оптимальной стратегии, то для второго игрока отклонения от его оптимальной стратегии не может быть выгодным. Отступление сторонами от их оптимальных стратегий ухудшает их собственное положение.

Пример 2.5.1. Решить матричную игру с платежной матрицей .

Решение. Этаматричная игра имеет размерность (3х4), т.Е. Игрок а имеет три стратегии, а игрок в – четыре. Запишем ее в нормальной форме.

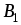
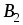
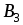
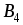
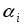
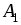
	3	2	5	7	2
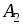
	5	4	6	5	(4)
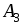
	2	3	1	6	1
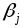
	5	(4)	6	7

Используя алгоритм принципа минимакса (максимина) имеем:

= max= max {2, 4,1} = 4,

= min= min {5, 4, 6, 7} = 4.

Поскольку , то эта игра определена в чистых стратегиях или является игрой с седловой точкой. Седловая точкаа₂₂ = (А₂,В₂) = 4, цена игры=4. Таким образом, совокупность оптимальных стратегийА₂иВ₂является решением игры.

Если игра не имеет седловой точки, то поиск решения игры приводит к применению слож­ной стратегии, состоящей в случайном применении двух и более чистых стратегий с определенными вероятностями. Такая сложная стратегия называется смешанной.

	Смешанной стратегией игроков А (В) называются выражения вида ,, где,,,, – вероятность использования чистой стратегии, – вероятность использования чистой стратегии.
Замечание.		Любая конченная игра имеет решение в чистых или смешанных стратегиях.

Матричные игры тесно взаимосвязаны с задачами линейного программирования.

Каждой матричной игре можно поставить в соответствие две двойственные задачи, отражающие интересы сторон.

Для игрока Азадачу записывают по столбцам, для игрокаВ- по строкам; знаки неравенств для игрокаАбудут “”, дляВ– “”. Правые части ограничений и коэффициенты целевых функций в обеих задачах равны 1, у задачи для игрокаАцель, у задачи для игрокаВ -max.

Для игрока АДля игрокаВ

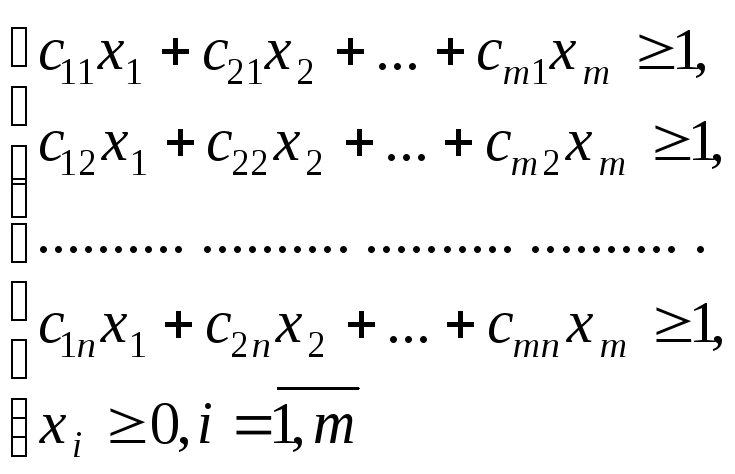
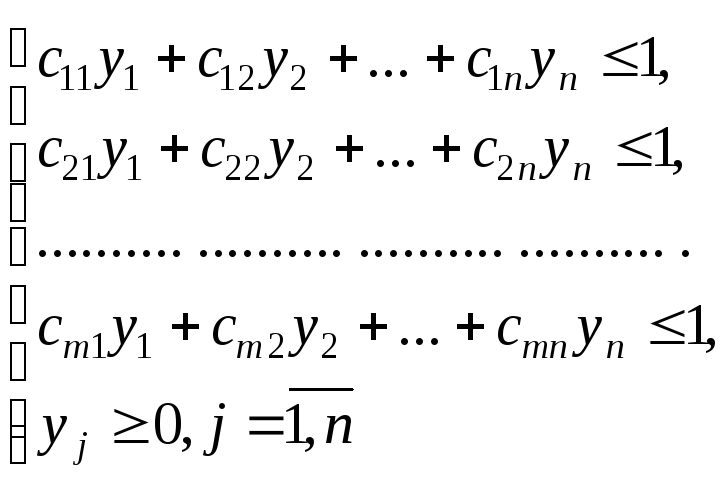
где ,,.
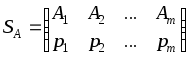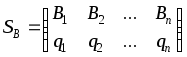