
- •Математическое моделирование Учебное пособие
- •Донецк 2006
- •Содержание
- •Введение
- •1. Построение экспериментальных законов распределения
- •1.1. Общие положения
- •1.2. Статистические критерии согласия
- •Г) Критерий согласия Романовского
- •1.3. Построение закона Пуассона
- •1.4. Построение показательного закона
- •1.5. Построение нормального закона
- •2. Модели оптимизации
- •2.1. Принципы формирования моделей оптимизации
- •Задача производственного планирования
- •Задача оптимальной загрузки оборудования
- •Задача о смесях
- •Транспортная задача
- •2.2. Графический метод решения задачи линейного программирования
- •Алгоритм графического метода решения злп
- •2.3. Универсальный метод решения линейных задач оптимизации
- •Алгоритм симплекс-метода решения злп
- •Пример 2.3.1. Решить злп (2.2.1), (2.2.5) симплекс-методом.
- •Критерий оптимальности опорного плана
- •Переход к следующей симплекс-таблице осуществляют по правилам:
- •2.4. Двойственная задача линейного программирования
- •Свойства двойственных задач
- •2.5. Методы анализа конфликтных ситуаций с помощью матричных игр
- •Алгоритм принципа максимина (минимакса)
- •Решение. Этаматричная игра имеет размерность (3х4), т.Е. Игрок а имеет три стратегии, а игрок в – четыре. Запишем ее в нормальной форме.
- •Последовательность действий при решении игры
- •3. Регрессионный анализ
- •3.1. Однофакторные модели
- •3.1.1. Построение однофакторных моделей
- •3.1.2. Оценка качества моделей
- •Свойства коэффициента корреляции
- •Построение доверительного интервала для прогнозного значения
- •Пример 3.1.Исследовать зависимость объема прибыли от количества торговых точек. Сделать прогноз в предположении, что количество торговых точек будет увеличено до 25.
- •Вспомогательная расчетная таблица
- •Пример 3.2.Исследовать зависимость показателяуи факторахс помощью логарифмической, степенной и полиномиальной регрессий.
- •3.1.3. Модели рядов динамики
- •3.2. Автокорреляция данных и остатков
- •3.2.1. Автокорреляция данных
- •Пример 3.4. Исследовать на автокорреляцию динамический ряд:
- •Вспомогательная таблица для расчета коэффициента автокорреляции
- •3.2.2. Автокорреляция остатков
- •Причины возникновения автокорреляции
- •Вспомогательная таблица для расчета d-статистики
- •С помощью формулы (3.2.2) найдем d -статистику:
- •3.3. Мультиколлинеарность
- •Причины возникновения мультиколлинеарности:
- •Методы исследования мультиколлинеарности
- •Меры по устранению мультиколлинеарности:
- •3.4. Множественная линейная регрессия
- •3.4.1. Построение множественной линейной регрессии
- •Расчет элементов коэффициента
- •3.4.2. Матричный подход
- •Построение корреляционной матрицы
- •Построение модели множественной линейной регрессии и ее анализ
- •3.4.4. Нелинейные модели
- •3.4.5. Эластичность
- •4.Экспертные оценки и элементы теории графов
- •4.1. Ранговая корреляция
- •4.1.1. Экспертное оценивание
- •4.1.2. Этапы работ в системе экспертных оценок
- •4.1.3. Метод ранговой корреляции
- •Вспомогательные расчеты
- •Б) Случай многих экспертов
- •4.2. Элементы сетевого планирования
- •Основные элементы сетевого графика
- •Основные требования к сетевой модели
- •5. Индивидуальные задания для самостоятельной работы студентов по курсу “математическое моделирование”
- •5.1. Задания к разделу “Построение законов распределения”
- •5.2. Задания к разделу “Математическое программирование”
- •5.3. Задания к разделу “Регрессионный анализ”
- •Задание 2.
- •Задание 3.
- •5.4. Задания к разделу “Экспертные оценки и элементы теории графов” Задание 1.
- •Значение критерия Пирсона
- •Критерий Колмогорова
- •Критерий Колмогорова
- •Квантили распределения Стьюдента
- •Коефициентов автокорреляции
- •Литература
- •Пеніна Галина Геннадіївна, канд. Екон. Наук, доцент
2.2. Графический метод решения задачи линейного программирования
Графический метод решения ЗЛП основан на утверждениях, приведенных в пункте 2.1. Согласно теореме 2, оптимальное решение находится в вершине области допустимых решений и поэтому решить ЗЛП – найти вершину области допустимых решений, координаты которой дают оптимальное значение целевой функции.
Графический метод используют для решения ограниченного класса задач с двумя переменными, иногда с тремя переменными. Надо заметить, что для трех переменных эта область является недостаточно наглядной.
Алгоритм графического метода решения злп
Построить прямые линии, уравнения которых получаем заменой в системе ограничений (2.1.2) знаков неравенств на знаки равенств.
Определить полуплоскости, соответствующие каждому неравенстве задачи.
Найти многоугольник решений ЗЛП, учитывая, что
 .
.Построить вектор направлений
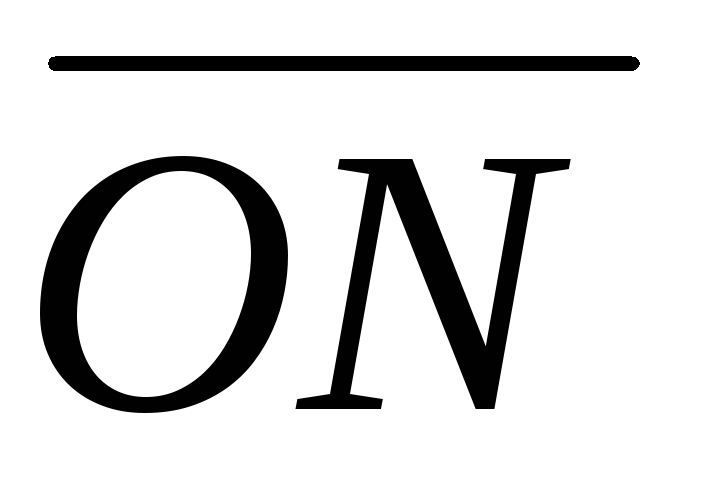 =(с1,с2),
который указывает направление наибольшего
возрастания целевой функции ЗЛП (2.1.1).
=(с1,с2),
который указывает направление наибольшего
возрастания целевой функции ЗЛП (2.1.1).Построить прямую z, которая проходит через область допустимых решений, перпендикулярно к вектору
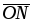 :
: .
Это линия уровня.
.
Это линия уровня.Переместить прямую
 в направлении вектора
в направлении вектора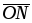 в случае максимизации целевой функции
(или в противоположном направлении в
случае минимизации целевой функции),
найти вершину многоугольника решений
ЗЛП, в которой целевая функция достигает
экстремального значения.
в случае максимизации целевой функции
(или в противоположном направлении в
случае минимизации целевой функции),
найти вершину многоугольника решений
ЗЛП, в которой целевая функция достигает
экстремального значения.Определить координаты точки, в которой целевая функция достигает оптимальное значения, и вычислить экстремальное значение целевой функции в этой точке.
Реализацию графического метода решения ЗЛП рассмотрим на примерах.
Пример 2.2.1. Решить ЗЛП графическим методом:
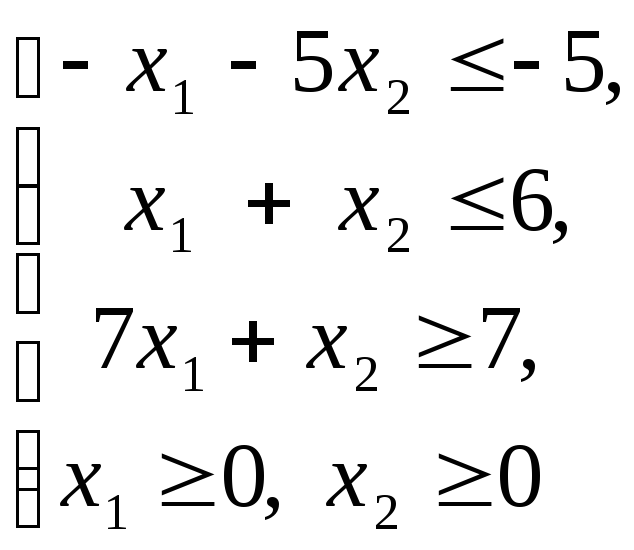 (2.2.1)
(2.2.1)
max z=x1+ 4x2(2.2.2)
Решение. Для построения области допустимых решений, которая состоит из пересечения полуплоскостей, соответствующих каждому неравенству системы ограничений (2.2.1), запишем уравнения граничных прямых:
l1: x1 + 5x2 = 5; l2: x1 + x2 = 6; l3: 7x1 + x2 = 7.
|
Замечание. |
Для удобства построения прямой линии, ее уравнение можно привести к виду в отрезках на осях
где параметры а,b– длины отрезков, отсекаемых прямой на соответствующих осяхОх1,Ох2 . |
|
Замечание. |
Если
уравнение прямой линии имеет вид:
|
Для
приведения уравнения прямой l1
к виду (2.2.3.) разделим
обе его части на 5:
![]() .
Таким образом, прямаяl1
отсекает на оси Ох1
5 единиц, на оси Ох2
1 единицу. Аналогично
имеем для l2:
.
Таким образом, прямаяl1
отсекает на оси Ох1
5 единиц, на оси Ох2
1 единицу. Аналогично
имеем для l2:
![]() иl3:
иl3:
![]() .
.
Для определения полуплоскостей, которые отвечают ограничениям системы (2.2.1), в ограничения нужно подставить координаты какой-либо точки, не лежащей на граничной прямой. Если получим верное неравенство, то все точки из этой полуплоскости являются решениями данного неравенства. В противном случае выбирают другую полуплоскость.
|
Замечание. |
В качестве точки сравнения целесообразно выбирать, если это возможно, точку О(0,0). |
Таким образом,
первая и вторая искомые полуплоскости
расположены в противоположную сторону
от начала координат (0 – 5·0![]() –
5; 7·0 + 0
–
5; 7·0 + 0![]() 7),
а вторая – в сторону начала координат
(0 + 0
7),
а вторая – в сторону начала координат
(0 + 0![]() 6). Область допустимых решений на рисунке
2.2.1 заштрихована.
6). Область допустимых решений на рисунке
2.2.1 заштрихована.
|
Замечание. |
В силу ограничений х1 |

Рисунок 2.2.1 – Область допустимых решений
Для
нахождения оптимального плана, который
будет находиться в вершине многоугольника
решений, нужно построить вектор
направлений
![]() =(с1,с2),
который указывает направление наибольшего
возрастания целевой функцииz=с1х1+с2х2.
=(с1,с2),
который указывает направление наибольшего
возрастания целевой функцииz=с1х1+с2х2.
В
данной задаче вектор направлений
![]() =
(1, 4): он начинается в точкеО(0,0) и
заканчивается в точкеN(1, 4).
=
(1, 4): он начинается в точкеО(0,0) и
заканчивается в точкеN(1, 4).
Далее
строим прямую, которая проходит через
область допустимых решений, перпендикулярно
к вектору
![]() ,
и называетсялинией уровня целевойфункции.Передвигаем линию
уровня в направлении вектора
,
и называетсялинией уровня целевойфункции.Передвигаем линию
уровня в направлении вектора![]() в случае максимизации целевой функцииzи в направлении противоположном
в случае максимизации целевой функцииzи в направлении противоположном![]() ,
в случае минимизацииz, до последнего
пересечения с областью допустимых
решений. В результате определяется
точка или точки, где целевая функция
достигает экстремального значения, или
устанавливается неограниченность
целевой функцииzна множестве
решений задачи.
,
в случае минимизацииz, до последнего
пересечения с областью допустимых
решений. В результате определяется
точка или точки, где целевая функция
достигает экстремального значения, или
устанавливается неограниченность
целевой функцииzна множестве
решений задачи.
Таким образом, точкой максимума целевой функции zявляется точкаАпересечения прямыхl2иl3.
Для вычисления оптимального значения целевой функции z найдем координаты точки А. Поскольку точка А – это точка пересечения прямых l2 и l3, то ее координаты удовлетворяют системе уравнений, составленной из уравнений соответствующих граничных прямых:

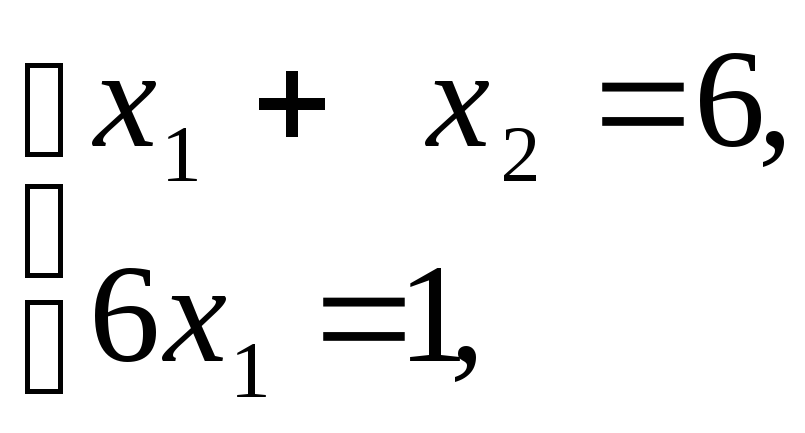
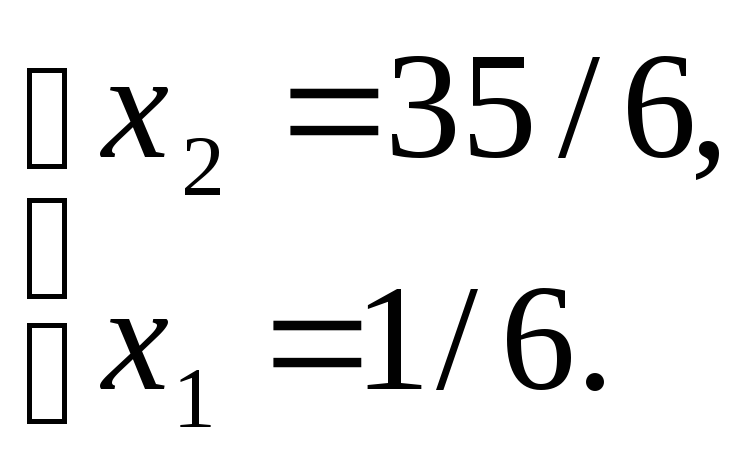
Таким образом, точка А имеет координаты x1 =1/6, x2 = 35/6.
Для вычисления оптимального значения целевой функции нужно подставить в нее координаты точки А.
Подставив координаты точки А в целевую функцию (2.4), получим
max z = 1/6 + 4·(35/6) = 47/2.
Пример 2.2.2. Построить на плоскости область допустимых решений системы линейных неравенств (2.2.4) и найти наибольшее и наименьшее значения целевой функции (2.2.5):
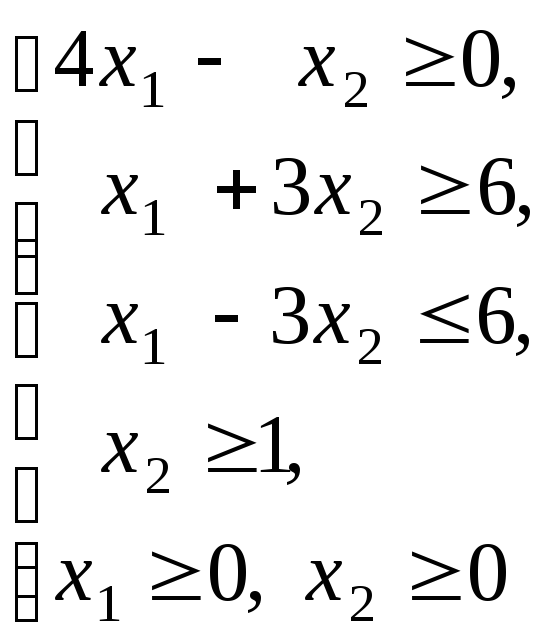 (2.2.4)
(2.2.4)
z= –2x1–x2(2.2.5)
Решение. Для построения области допустимых решений, которая состоит из пересечения полуплоскостей, соответствующих каждому неравенству системы ограничений (2.2.4), запишем уравнения граничных прямых:
l1: 4x1 – x2 = 0; l2: x1 + 3x2 = 6; l3: x1 – 3x2 = 6; l4: x2 = 1.
Прямая l1 проходит через точку с координатами (0;0). Для ее построения выразим x2 через x1: x2 = 4x1. Найдем еще одну точку, через которую проходит прямая l1 , например (1;4). Через точку с координатами (0;0) и точку с координатами (1;4) проведем прямую l1 .
Для
приведения уравнения прямой l2
к виду в отрезках на
осях (2.2.3) разделим обе его части на 6:
![]() .
Таким образом, прямаяl2
отсекает на оси Ох1
6 единиц, на оси Ох2
- 2 единицы. Аналогично
имеем для l3:
.
Таким образом, прямаяl2
отсекает на оси Ох1
6 единиц, на оси Ох2
- 2 единицы. Аналогично
имеем для l3:
![]() и Прямаяl4
параллельна оси Ох1
и проходит через точку с координатами
(0;1) .
и Прямаяl4
параллельна оси Ох1
и проходит через точку с координатами
(0;1) .
Для
определения полуплоскостей, которые
отвечают ограничениям системы (2.2.4) в
ограничения нужно подставить координаты
какой-либо точки, не лежащей на граничной
прямой. В силу ограничений х1![]() 0,х2
0,х2![]() 0, область допустимых решений ЗЛП лежит
в первой четверти координатной плоскости.
0, область допустимых решений ЗЛП лежит
в первой четверти координатной плоскости.
О бласть
допустимых решений на рисунке 2.2.2
заштрихована.
бласть
допустимых решений на рисунке 2.2.2
заштрихована.
Рисунок 2.2.2 – Область допустимых решений
Построим
вектор направлений
![]() =
(–2,–1). Далее строим линию уровня,
перпендикулярно к вектору
=
(–2,–1). Далее строим линию уровня,
перпендикулярно к вектору![]() .
.
Для
нахождения наибольшего значения целевой
функции передвигаем линию уровня в
направлении вектора
![]() до последнего пересечения с областью
допустимых решений. Таким образом,
точкой максимума целевой функцииzявляется точкаА(пересечение прямыхl1иl2).
до последнего пересечения с областью
допустимых решений. Таким образом,
точкой максимума целевой функцииzявляется точкаА(пересечение прямыхl1иl2).
Для вычисления оптимального значения целевой функции zнайдем координаты точкиА. Поскольку точкаА– это точка пересечения прямыхl1иl2, то ее координаты удовлетворяют системе уравнений, составленной из уравнений соответствующих граничных прямых:



Таким образом, точка А имеет координаты x1 =6/13, x2 = 24/13.
Подставив координаты точки А в целевую функцию (2.2.5), получим оптимальное значение целевой функции
max z= – 2·(6/13) – (24/13) = – 36/13.
Для
нахождения наименьшего значения целевой
функции передвигаем линию уровня в
направлении, противоположном вектору
![]() до последнего пересечения с областью
допустимых решений. В этом случае целевая
функция неограниченна в области
допустимых решений, т.е. ЗЛП минимума
не имеет.
до последнего пересечения с областью
допустимых решений. В этом случае целевая
функция неограниченна в области
допустимых решений, т.е. ЗЛП минимума
не имеет.
В результате решения ЗЛП возможны следующие случаи:
Целевая функция достигает оптимального значения в единственной вершине многоугольника решений;
Целевая функция достигает оптимальное значение в любой точке ребра многоугольника решений (ЗЛП имеет альтернативные опорные планы с одинаковыми значениями z);
ЗЛП не имеет оптимальных планов;
ЗЛП имеет оптимальный план в случае неограниченной области допустимых решений.
