4.3 Пружні потенціали

Введемо тепер у розгляд допоміжні функції – потенціали.

Вектор зв’я заний умовою

Цій умові можна задовольнити, прийнявши

_, (4.15)

де - скалярна функція.

З векторної алгебри відомо, що для скалярної функції

Функція , яка задовольняє рівнянню (4.15), називається потенціальною, а – скалярним потенціалом силового поля. В задачах теорії пружності  називають також поздовжнім потенціалом або потенціалом поздовжньої хвилі.

Покажемо, що скалярний потенціал задовольняє хвильовому рівнянню (4.10):

Оскільки

то рівняння (4.10) прийме вигляд

або

,

або змінивши порядок диференціювання

Для виразу у круглих дужках можна прийняти

(4.16)

Отримане рівняння для скалярного потенціалу  є рівняння хвильового типу.

Розглянемо переміщення в пружньому тілі, які не супроводжуються обертами. В цьому випадку таі векторне рівняння руху (4.9) прийме вигляд

.

Оскільки згідно (4.8)

,

то зміщення задовольняють хвильовому рівнянню

(4.17)

Всі три рівняння: для дилатації (4.10), для скалярного потенціалу(4.16) і для пружних зміщень (4.17) описують процес розповсюдження поздовжньої хвилі.

З іншого боку, розглянемо вектор з обмеженням , що означає відсутність при деформаціях зміни елементарних об’ємів тіла. Вектор такого поля переміщень можна визначити через ротор векторної функції:

(4.18)

для якої

Вектор називають векторним потенціалом або потенціалом поперечної хвилі. Поле такого вектора називається вихровим.

Підставляючи (4.18) в рівняння руху (4.9)

і враховуючи, що та згідно (4.8)

отримаємо

(4.19)

Виконаємо над (4.19) операцію rot і, змінивши порядок диференційних операцій, отримаємо

(4.20)

Згідно (4.8) і рівняння (4.20) прийме вигляд

звідки

.

Ми задовольнимо цьому рівнянню, якщо покладемо

(4.21)

Повертаючи (4.14), (4.21) і (4.22), робимо висновок, що всі три рівняння однотипні і описують процес розповсюдження поперечної хвилі.

Отже, представляючи векторну функцію й у вигляді суми

,(4.23)

де і- скалярний та векторний потенціали, рівняння руху ізотропного однорідного пружного середовища (4.4) розкладається на два незалежних руху. Перший з них пов’язаний із зміною елементарних об’ємів речовини – стисненням або розтягом – і відповідає поздовжній хвилі. Для другого характерні оберти елементарних об’ємів, а розповсюдження цього виду деформації відповідає поперечній хвилі. Таким чином, з кожним типом хвиль пов’язаний певний вид пружної деформації. Швидкість розповсюдження окремого типу деформації залежить від коефіцієнтів а і b, хвильових рівнянь:

;

.

Відношення

(4.24)

і залежить від коефіцієнта Пуассона . Це означає, що поздовжня хвиля розповсюджується з більшою швидкістю ніж поперечна.

Для більшості гірських порід коефіцієнт Пуассона змінюється в границях 0,15<<0,5.

Наприклад, для =0,25 (гіпотеза Пуассона) , що відповідає міцним матеріалам (сталь, скло) і породам на значній глибині.

4.4 Cферичнi хвилі

Явища розповсюдження хвиль таких, як світло, звук або пружних, описуються хвильовим рівнянням. Для розуміння фізичного смислу хвильових рівнянь проаналізуємо їх рішення.

Спочатку розглянемо простий ідеалізований випадок „одномірної хвилі”, коли положення точки або інша властивість залежить від одної координати хі часуt. Така функціяU(x,y)задовольняє хвильовому рівнянню виду

. (4.25)

Для знаходження загального рішення перейдемо до нових незалежних змінних

, .

Знайдемо похідні функції :

;

;

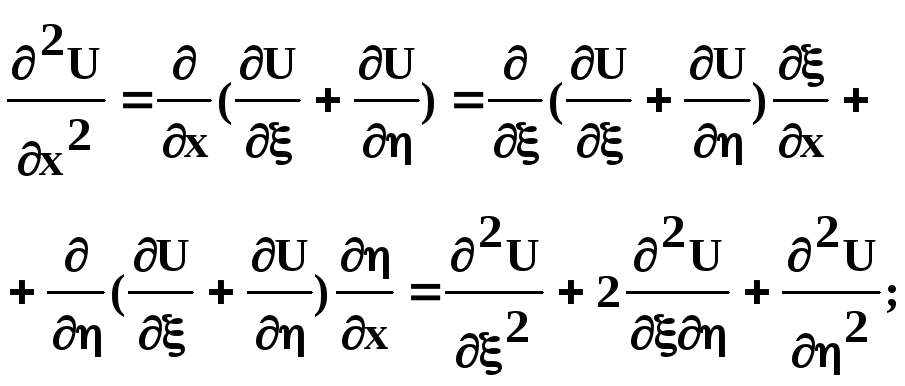
і підставимо їх в рівняння (4.25). В результаті отримаємо хвильове рівняння:

(4.26)

загальним рішенням якого є функція . Оскільки (4.26) є наслідком (4.25), то загальним рівнянням (4.26) буде функція

; (4.27)

де функція описує хвильовий процес, який розповсюджується в напрямі осіх, а функція- хвилю, яка рухається в зворотному напрямі.

Знайдемо частковий розв’язок хвильового рівняння, який задовольняє початковим умовам

Перша умова дає рівняння

(4.28)

Для другої умови отримаємо диференційне рівняння

інтегрування якого дає

(4.29)

З врахуванням (4.28) та (4.29) частковий розв’язок хвильового рівняння буде таким

(4.30)