Проаналізуємо четверту модель. Її хвильовому рівнянню

(6.27)

відповідає рівняння стану середовища

. (6.28)

Перетворимо (6.28) аналогічно (6.25) і отримаємо

(6.29)

або

(6.29’)

При з (6.29) маємо

, (6.30)

тобто залишкова деформація пропорційна похідній по часу від напруження. Співвідношення (6.30) вказує на те, що площа петлі гістерезіса в момент часу, коли , контролюється похідною напруження, оскільки зв’язок деформації з напруженням у цей момент часу неможливий. Із співвідношення (6.30) слідує ще один важливий висновок - коефіцієнтbне може бути постійною величиною. У протилежному випадку величина залишкової деформації при збільшенніможе перебільшити величину деформації, яка викликається максимальним напруженням. Оскільки похідна, якщо, коефіцієнтbповинен бути обернено пропорційним до. З врахуванням цього рівняння (6.27) набуде вигляду

, (6.31)

де . Тут знак мінус вибраний тому, що у виразі (6.30) знак залишкової деформації повинен бути зворотним знаку похідної напруження. Підставляючизамістьbу таблиці 6.2, отримаємо для коефіцієнта поглинання

. (6.32)

Таким чином, ми отримаємо вираз для , який повністю відповідає експериментальним даним, - коефіцієнт поглинання прямо пропорційний до частоти коливань та обернено пропорційний до швидкості поширення пружних хвиль.

Слід відмітити, що для фізичної реалізації тої чи іншої моделі середовища необхідно виконання критерію Пейлі-Вінера, за яким коефіцієнт поглинання не може бути функцією частоти в усьому діапазоні частот. Отриманий тут коефіцієнт поглинання (6.32) віддзеркалює процес дисипації енергії за рахунок залишкової деформації тіла в процесі поширення пружних хвиль, а коефіцієнт bобернено пропорційний межі текучості матеріалу. Відомо, що ця межа залежить від швидкості деформації. Зменшення пластичних деформацій із зростанням частоти “вимикає” механізм поглинання пружних хвиль за верхньою межею сейсмічного (а, можливо, і акустичного) діапазону. Іншими словами, для задоволення критерію Пейлі-Вінера достатньо припуститипри.

Таким чином, отримане хвильове рівняння (6.31) має мінімальне число параметрів (сіb), містить лише одну другу похідну поля зміщення, добре узгоджується з експериментальними даними та може, по О.К.Кондратьєву, називатись оптимальним хвильовим рівнянням. Перевага (6.31), перш за все, в більш простому вигляді і наявності лише однієї другої похідної. Причому це похідна по часу і її обчислення не складає таких проблем, як других просторових похідних, оскільки крок реальних сейсмічних даних поt більш кореспондує з заміною похідних на кінцеві різниці, ніж крок поx. Отже, запропоноване хвильове рівняння (6.31) є кращою основою для побудови кінцево-різницевих схем міграції даних сейсморозвідки для реальних (поглинаючих) середовищ.

7 Комплексні хвильові рівняння

Напрям сейсморозвідки, що бурхливо розвивається, - прогнозування геологічного розрізу - висуває завдання вирішення все більш тонких інтерпретаційних питань, детального аналізу хвильового поля. Природно, що, вирішуючи завдання прогнозу колекторських властивостей гірських порід , їх флюїдовмісту, не можна залишатись у рамках гуківської моделі ідеально пружного тіла, яка описується хвильовим рівнянням Ламе. Тому є зрозумілим інтерес сейсморозвідників до створення таких моделей середовищ, які б враховували непружне поглинання сейсмічної енергії та слабку дисперсію швидкостей пружних хвиль , які спостерігаються на практиці. Створюючи моделі поширення хвиль у флюідонасиченних породах, дослідники (М. Біот, Р. Столл) йшли класичним шляхом: враховуючи обмеження на поле зміщень, обумовлене перетіканням рідини у поровому просторі, отримували вираз для деформацій елемента об'єму, враховували зв'язок деформацій та напружень, підставивши, які у рівняння руху , отримували хвильове рівняння. При цьому хвильові рівняння в силу специфіки виводу, обов'язково містили другі часткові похідні від поля зміщень по часу та простору, обумовлюючи хвильовий процес, а також непарні похідні, які містять похідну по часу і є дисипативними членами у хвильовому рівнянні. Загальним недоліком отриманих таким чином хвильових рівнянь є те , що вони добре описують процес поширення пружних хвиль лише в окремих інтервалах частот. Так , модель Р. Столла чудово узгоджується з експериментальними даними багатьох дослідників в діапазоні частот 10-100 кГц, але в сейсмічному діапазоні частот вимагає квадратичної залежності коефіцієнта поглинання від частоти, що суперечить польовим спостереженням. Спроби краще узгодити модель з експериментом приводять до невиправданого ускладнення хвильового рівняння, збільшенню числа параметрів реологічної моделі середовища .

Разом з тим існують більш прості, ніж виведені з рівняння стану, хвильові рівняння. Нами була здійснена спроба синтезу останніх, виходячи з заданих властивостей дисперсійного співвідношення. Однак, формальне конструювання хвильових рівнянь часто приводить до нефізичних рівнянь стану та дисперсійних співвідношень, які не відповідають даним експерименту.

Нижче ми спробуємо узгодити формальний синтез хвильового рівняння з фізично обґрунтованими обмеженнями на поле зміщень у флюідонасиченній проникній гірській породі.

Згідно з Дж.Уіземом хвильовий процес будемо описувати рівнянням

, (7.1)

де U_t та U_х - відповідно похідні по часу і простору*, с- коефіцієнт хвильового рівняння, який має розмірність швидкості.

Щоб накласти обмеження на поле зміщень, використаємо закон Дарсі

, (7.2)

де v - швидкість перетікання флюїду з в'язкістюв поровому просторі гірської породи з проникністюk,р_х -градієнт тиску , який викликає це перетікання. Оскільки при розповсюдженні хвиль утворюються зони стиску та розтягу у гірській породі , виникають узгоджені з полем зміщень градієнти тиску, які викликають перетікання флюїду в її порах. Природно припустити , що при інших рівних умовах перетікання флюїду тим більше , чим більше зміщення елемента гірської породи.

Припустимо, що швидкість v обернено пропорційна швидкості зміщення

(7.3)

тут ї далі для спрощення будемо розглядати плоскі хвилі, що розповсюджуються вздовж осі X, та одномірне хвильове рівняння.

Градієнт тиску при розповсюдженні хвиль пропорційний прискоренню елементарного об'єму середовища

, (7.4)

де _x - градієнт напруження, - щільність елемента породи. Враховуючи (7.3) та (7.4), перепишемо вираз (7.2) , який після інтегрування поtнабуде вигляду

(7.5)

Таким чином , із закону Дарсі (7.2) отриманий зв'язок (7.5) між зміщенням та його швидкістю при розповсюдженні хвиль у флюідонасиченній гірській породі.

Побудуємо тепер комплексну функцію, дійсна частина якої представлена виразом (7.1), а уявна - умовою (7.5). Остання не залежить від рівняння (7.1) так само , як уявна частина не залежить від дійсної. Цим, власне, і пояснюється використання комплексного представлення. Таким чином, суть нашої ідеї полягає в тому, що незалежна умова або обмеження на поле зміщень вводиться як уявна компонента у хвильове рівняння. Оскільки рівність нулю комплексного числа передбачає рівність нулю як дійсної , так і уявної частини останнього, запишемо

, (7.6)

де b і d - коефіцієнти , зв'язок яких з коефіцієнтами в рівнянні (7.5) буде встановлений пізніше.

Тепер отримаємо дисперсійне співвідношення для рівняння (7.6), вважаючи , що його елементарним рішенням є

, (7.7)

де К=k-і -комплексне хвильове число,k - його дійсна частина,- коефіцієнт поглинання. Підстановка (7.7) в рівняння (7.6) дає

, (7.8)

Вимога дійсності дисперсійного співвідношення приводить нас до системи

,(7.9)

розв’язуючи яку , отримаємо

(7.10)

(7.11)

(7.12)

Залежності (7.10) – (7.12) добре узгоджуються з експериментальними даними по залежностям коефіцієнта поглинання та швидкості пружних хвиль від частоти. З виразу (7.10) для коефіцієнту поглинання випливає, що коефіцієнт bповинен мати розмірністьрад^-1,а з формули (7.11) витікає, щоdмає розмірністьрад/c.Тепер, порівнюючи (7.5) та уявну частину рівняння (7.6) , отримаємо значення коефіцієнтівbіdз врахуванням їх розмірності.

(7.13)

Зауважимо, що ліву та праву частину співвідношення (1.5) довелося помножити на постійну частоту ₀ . Отож, ми отримали, що коефіцієнт поглинання лінійно залежить від частоти, обернено пропорційний швидкості поширення хвиль (груповій швидкості (1.12)), що добре узгоджується з даними багатьох дослідників. Поглинання хвиль тим більше , чим більша проникність породи , та менше в'язкість флюїду, який її насичує. Це добре пояснює різке поглинання сейсмічних хвиль у межах газонасиченої частини пласта в порівнянні з його водонасиченою частиною. Збільшення щільності породи, при інших рівних умовах, приводить до збільшення градієнта тиску, отож флюїд перетікає у поровому просторі з більшою швидкістю і збільшуються теплові втрати енергії. Нарешті, коефіцієнт поглинання пропорційний₀. . Фізичний зміст цього коефіцієнта нам поки що невідомий. Можливо, він відображає особливості структури порового простору. Цей коефіцієнт можна використовувати для узгодження значень проникності, в'язкості та щільності, з коефіцієнтом поглинання.

Фазова швидкість (7.11) монотонно зростає із зростанням частоти, асимптотично наближуючись до групової. Дисперсія фазової швидкості визначається величиною коефіцієнта d, і зростає з його збільшенням. Експериментально спостерігається незначне зростання швидкості при зміні частоти з 10 Гц до10 кГц. Якщо рахувати, що зміщення флюїду відносно скелету гірської породи складає порядку 0.1 зміщення елемента гірської породиU, то величина₀ повинна бути співрозмірна з нижньою частотою сейсмічного діапазону.

Тепер розглянемо рівняння стану середовища, яке відповідає хвильовому рівнянню (7.6). Щоб перейти від нього до рівняння стану , використаємо співвідношення таде- деформація гірської породи.

(7.14)

Проінтегруємо вираз (7.14) по х

(7.15)

Перед тим , як продиференціювати інтеграл (7.15) по t, замінимо інтеграл по Х на інтеграл по t

при с=соnst,

оскільки графік хвилі розвернутий на 180° до її профілю.

Далі отримаємо

(7.16)

Таким чином, комплексному хвильовому рівнянню (7.6) відповідає комплексне рівняння стану (7.16). Виділивши дійсну і уявну частини,

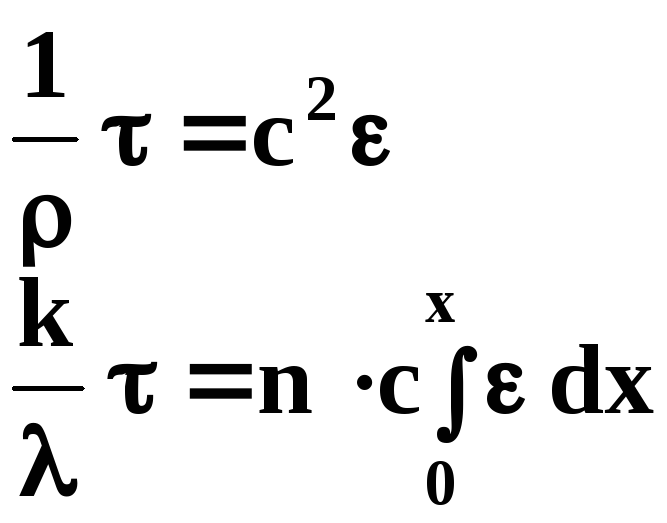(7.17)

Із другого виразу (7.17) можна отримати інтегральне рівняння

, (7.18)

яке має рішення

(7.19)

Вираз (7.19) свідчить, що деформація у гірській породі, що описується рівнянням стану (7.16), зменшується з плином часу по експоненціальному закону.

Таким чином , деформація змінюється пропорційно напруженню , а коливний процес затухає тим швидше , чим менше інертність елемента гірської породи, яка визначається його щільністю , та чим більше в'язкість флюїду, який насичує поровий простір. На швидкість затухання коливань впливає проникність породи так само, як і проникність перепускних отворів у гідроамортизаторах.

Вищевикладене дозволяє зробити висновок, що хвильове рівняння (7.6) , яке синтезовано за допомогою додаткових обмежень на комплексній площині, добре узгоджується з даними експериментів по визначенню коефіцієнтів поглинання та дисперсії швидкості пружних хвиль, дає фізичне пояснення процесам затухання сейсмічних коливань у флюідонасичених породах.