1.3 Зв’язок між компонентами малої деформації та її

головними коефіцієнтами

Встановимо взаємозв’язок між компонентами малої деформації при переході від системи координат x, y, zдо системи 1, 2, 3, вісі якої суміщені з головними вісями деформації.

Позначимо косинуси кутів між віссю 1 та вісями x, y, z через,,, віссю 2 з тими же вісями,,, віссю 3 також з вісямиx, y, zчерез,,. Ці позначення зведемо в таблицю.

Таблиця 1.1 - Спрямовуючі косинуси координатних

вісей

Вісі	x	y	z
1				’
2				’
3				’
				Орти

Позначимо напрямки вісей x, y, z одиничними векторами, а вісей 1, 2, 3 - векторами. Зрозуміло, що таблиця косинусів в той же час є таблицею складових векторівпо осях 1, 2, 3 та векторівпо вісяхx, y, z.

У системі координат x, y, zскладові векторавизначаються виразом (1.9):

У системі координат 1, 2, 3 складові вектора можна записати у відповідності до (1.20):

Представимо складові вектора по вісяхx, y, z як скалярні добутки векторана вектора, які потім розгорнемо по складовим векторів на вісі 1, 2, 3. В результаті отримаємо:

(1.21)

(1.22)

(1.23)

Таким самим чином можна представити складові вектора по вісяхx, y, z.Розгорнувши скалярні добутки векторана векторипо складовим цих векторів на вісі 1, 2, 3, отримаємо:

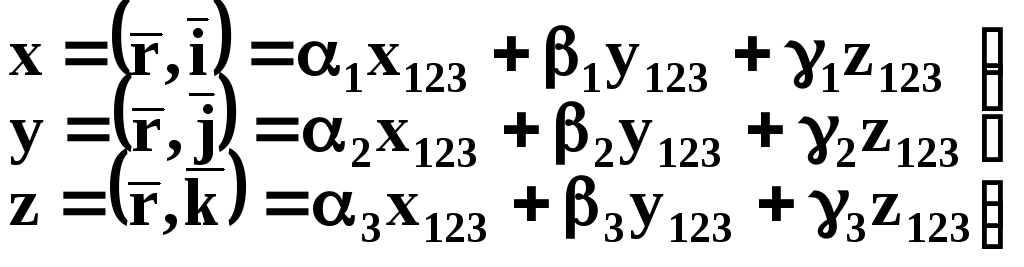(1.24)

На підставі (1.21), (1.24), та (1.20) перше рівняння системи (1.9) можна представити у вигляді:

або

Останній вираз мусить задовольнятись при довільних значеннях x₁₂₃, y₁₂₃, z_123.Це означає, що коефіцієнти приx₁₂₃, y₁₂₃, z₁₂₃ в правій та лівій частинах рівні між собою, тобто

(1.25)

(1.26)

(1.27)

З рівнянь (1.25) - (1.27) можна отримати, використовуючи добутки спрямовуючих косинусів з таблиці 1.1,

(1.28)

(1.29)

. (1.30)

Так само можна встановити зв’язок між компонентами деформації та головними коефіцієнтами. Для цього необхідно підставити в друге та третє рівняння системи (1.9) значеннятаз (1.22) та (1.23),x, y, zз (1.24) таз (1.20). В результаті отримаємо

(1.31)

(1.32)

(1.33)

Формули (1.28) - (1.33) пов’язують компоненти малої деформації відносно довільних вісей x, y, z через головні коефіцієнти деформації та косинуси кутів між цими вісями та головними вісями деформації.

1.4 Фізичний зміст компонент малої деформації

Для з’ясування фізичного змісту компонент деформації розглянемо декілька практичних випадків.

1.4.1 Візьмемо тонкий брусок, який витягнутий вздовж вісі x (дивись рисунок 1.3).

0 z

a

M a+x

y U_ox

N

U_x=U_ox+

x

F

Рисунок 1.3 - Одноосний розтяг бруска вздовж вісі x

На довгому ребрі бруска відмітимо точки M(a)таN(a+x). Якщо розтягувати брусок силоюFвздовж вісіx, то компоненти зміщенняU_y та U_zточкиNбудуть рівні нулю. Як слідує з рисунка 1.3 та рівняння (1.3) величина

(1.34)

уявляє відносну зміну розміру тіла (розтяг або стиск) вздовж вісі x.Аналогічнота- відносні зміни розмірів тіла вздовж відповідно вісейутаz.

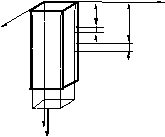
1.4.2 Виріжемо в пружному тілі прямокутний паралелепіпед таким чином, щоб він до деформації лежав би на головних вісях деформації 1, 2, 3 та мав ребра довжиною ,,

1

2

3

Рисунок 1.4 - Об’ємна деформація прямокутного паралелепіпеда

Tоді його об’єм до деформації буде . Після деформації, коли кінці ребер паралелепіпеда будуть переміщені вздовж головних вісей на, його об’єм буде дорівнювати

(1.35)

Нехтуючи об’ємом відокремлених на рисунку 1.4 брусочків, які є малими другого степеня, та кубічка, об’єм якого є малою величиною третього степеня, тобто відкидаючи добутки коефіцієнтів з (1.35), отримаємо

. (1.36)

Відношення приросту об’єму до початкового об’ємуV називається об’ємною деформацією або дилатацією  . Розкриваючи зміст , зауважимо, що головні коефіцієнти деформації є відношення приростків відрізків вздовж вісей 1, 2, 3 до їх початкової довжини.

Об’ємну деформацію можна представити інакше. Додамо рівняння (1.28), (1.31), (1.32) та візьмемо до уваги, що

. Тоді отримаємо

(1.43)

Таким чином, об’ємна деформація (дилатація) рівна дивергенції вектора зміщення .

1.4.3 Виріжемо в пружному тілі тонку пластинку прямокутної форми та розташуємо її в площині xoz (див. рисунок 1.5).

z

x₁

x F

А В

A^/B^/



z

0 C

x

x

Рисунок 1.5 – Деформація зсуву

Розміри пластинки до деформації позначимо через x та z. Нижнє ребро пластинки закріплене вздовж вісі x, а до її верхнього ребра по дотичній прикладена силаFпаралельно вісіx. Під дією цієї сили пластинка займе нове положення 0A^/B^/C. За умовами задачіy=y₁=0. Оскільки деформація мала, можна рахувати, що величинапри деформації не змінюється, а відносні зміни розмірів вздовж вісіxвідсутні. Таким чином, система (1.7) набуває вигляду:

Звідси

Звертаючись до рисунка 1.5, можна записати

(1.38)

Аналогічно величина

, (1.39)

де - кут між віссю xта стороною 0С при деформуючій силі, яка скерована вздовж вісіz, якщо пластинка була б закріплена по стороні 0А.

Таким чином величина

(1.40)

уявляє собою зміну початкового кута між сторонами 0А та 0С після деформації в площині xoz. Так самота- компоненти деформації зсуву в площинахxoy таyoz.

Зауважимо, що при деформаціях зсуву об’єм тіла не змінюється, а змінюється лише його форма.

Матриця коефіцієнтів деформації

(1.40)

називається тензором деформації.

Що таке тензор? Тензор - це сукупність взаємопов’язаних величин. Так три скаляри - координати точки в просторі - утворюють вектор або тензор першого рангу, оскільки вони пов’язані з просторовим розташуванням однієї точки, а інші три скаляри - вага кавуна, розмір взуття бравого солдата Швейка та відстань від Вашого дому до Києва - не утворюють тензора першого рангу, оскільки це не взаємопов’язані величини.

Сукупність взаємопов’язаних векторів утворює тензор другого рангу. Саме таким тензором є матриця (1.41). До речі, вперше поняття тензору було введено саме в теорії пружності, а вже пізніше сформувався окремий розділ математики - тензорний аналіз. В межах даного курсу досить знати дві основні властивості тензору другого рангу:

- тензор вісесиметричний, тобто елементи, які лежать по різні боки від головної діагоналі матриці на рівних відстанях від неї, попарно рівні ;

- слід тензора ( або сума компонент, які лежать на головній діагоналі тензора) інваріантний відносно системи координат, тобто її зміна не впливає на його значення.

До властивостей тензорів другого рангу ми повернемось, коли будемо розглядати тензор напруження.