1 Пружні деформації

1.1 Мала деформація та її компоненти

У пружному тілі під дією прикладених сил відбуваються зміни відстаней між точками або кутів між лінійними елементами, які мають спільну точку. Це явище називається деформацією твердого тіла. В сейсморозвідці пружні хвилі збуджуються вибухами або потужними ударними, або вібродіями на ґрунт. На значних віддалях від джерела хвиль гірські породи поновлюють свою первісну форму та об’єм миттєво, одразу після припинення дії сил, які викликали деформацію. Такі деформації називають малими. При їх вивченні нехтують другими та вищими степенями зміни віддалей між точками. Часто такі деформації називають лінійними або гуківськими деформаціями. Біля потужного джерела пружних хвиль, коли гірські породи не поновлюють свій об’єм та форму, мають місце залишкові деформації. В цьому випадку говорять про пластичні деформації тіла. До таких деформацій ми повернемось в другій частині курсу, а поки що будемо вважати, що всі деформації є малими.

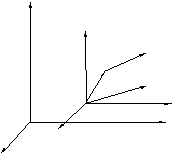
Віднесемо тверде абсолютно пружне тіло до прямокутних осей координат x’,y’,z’ (дивись рисунок 1.1). Для дослідження деформації, яка відбувається в тілі, розглянемо досить близьку до довільної точки 0 тіла точку А. Вектор з точки 0 до точки А позначимо через r. В результаті деформації тіла точки 0 та А отримали переміщенняU_oта U. Будемо вважати, що ці переміщення змінюються при переході від одних точок тіла до інших і є функціями їх координат. Тоді, позначивши координати точки 0 черезa,b,c,точки А черезa+x, b+y, c+z,складові переміщень точок 0 та А можна визначити за формулами:

U_ox=f₁(a,b,c),

U_oy=f₂(a,b,c), (1.1)

U_oz=f₃(a,b,c).

U_x=f₁(a+x,b+y,c+z),

U_y=f₂(a+x,b+y,c+z), (1.2)

U_z=f₃(a+x,b+y,c+z).

z’

z

U

A

r

U_o

0 y

0’ y’

х

x’

Рисунок 1.1 - Переміщення вектора rв нерухомійx’,y’,z’ та рухомійx,y,z системах координат

Розкладемо (1.2) в ряд Тейлора. Зважаючи на (1.1) та обмежуючись малими першого порядку відносно малих приростів координат x,y,z,отримуємо:

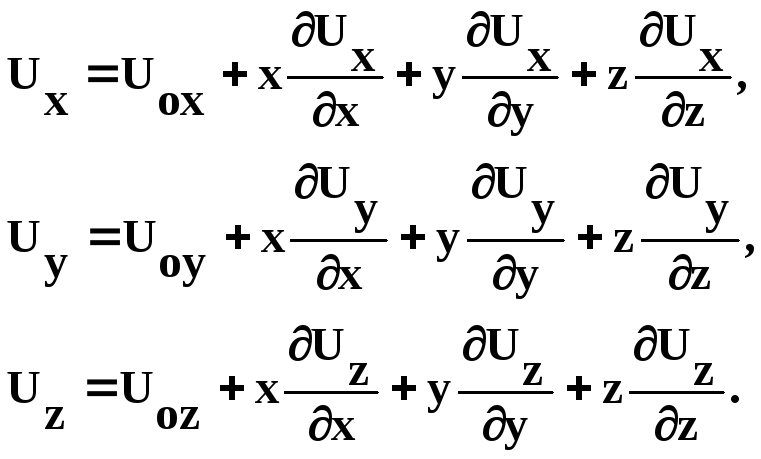(1.3)

Введемо в розгляд рухому систему координат x, y, z, початок якої переміщується разом з точкою 0 пружного тіла, а вісі лишаються колінеарними нерухомим вісямx’, y’, z’ (дивись рисунок 1.1).

У новій системі координат складові переміщення точки 0 дорівнюють нулю, а складові переміщення будь-якої іншої точки пружного тіла відносно точки 0 будуть рівні:

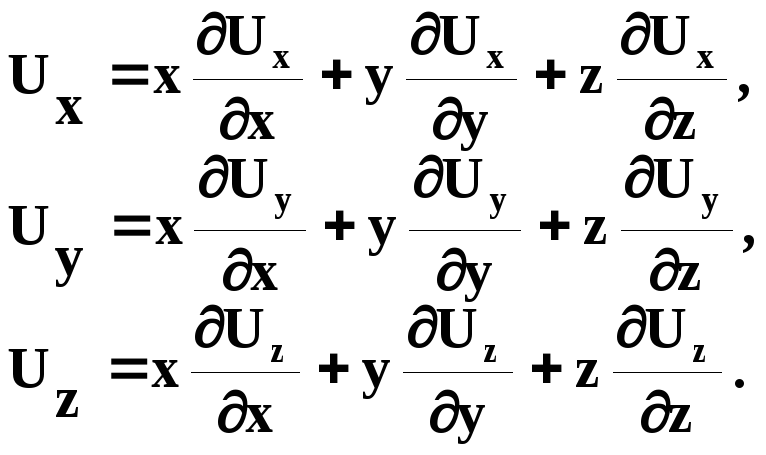(1.4)

Таким чином, якщо до деформації положення точки Авизначалось координатамиx, y, z,то після деформації, коли точка отримала переміщенняз складовимиU_x, U_y, U_z, її координати в рухомій системі будуть:

x₁=x+U_x,

y₁=y+U_y, (1.5)

z₁=z+U_z.

Беручи до уваги (1.4), отримаємо:

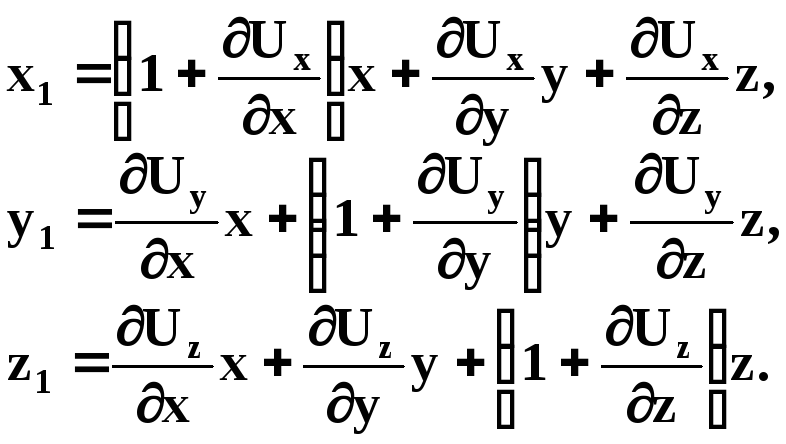(1.6)

з(1.6) випливає, що координати точки А до і після деформації пов’язані лінійною залежністю. Така деформація називається однорідною.

Виконаємо над (1.6) арифметичні перетворення. Додамо до обох частин першого рівняння (1.6) величини тапісля чогоx₁запишемо в наступному вигляді:

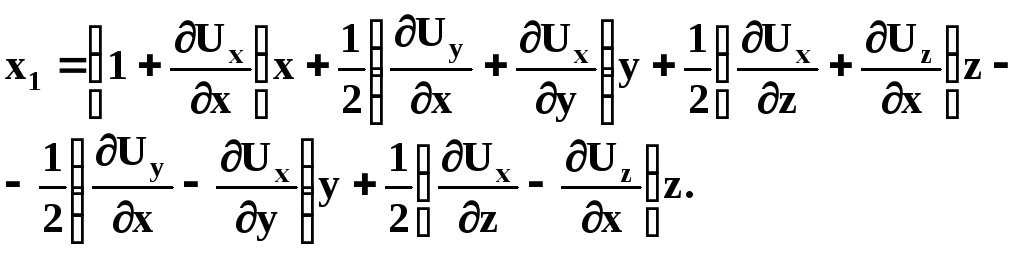Аналогічно перетворимо інші рівняння системи (1.6). Для спрощення запису введемо наступні позначення:

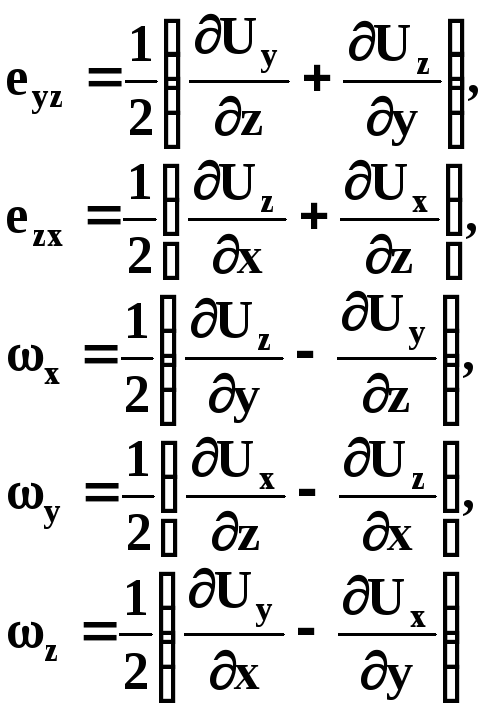
Після перетворень з врахуванням введених позначень система (1.6) буде записана так:

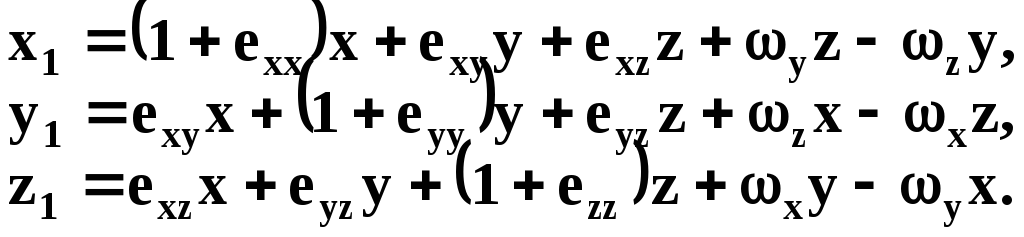(1.7)

Величини називаються компонентами малої деформації, а величиникомпонентами елементарного обертання.

Запишемо систему (1.7) в наступному вигляді:

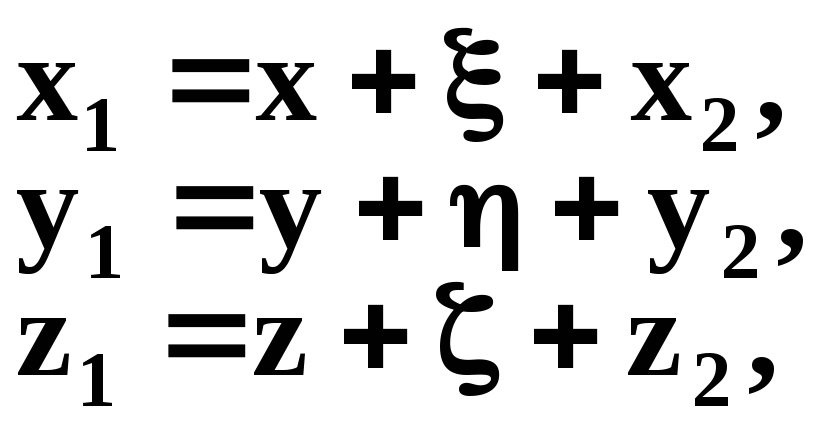(1.8)

де

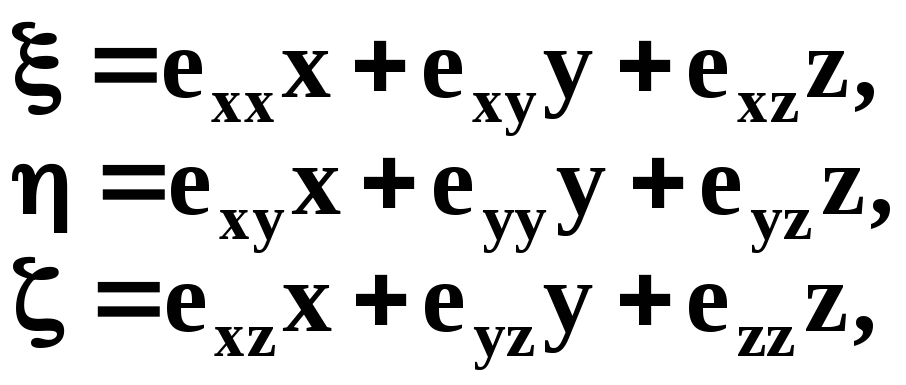(1.9)

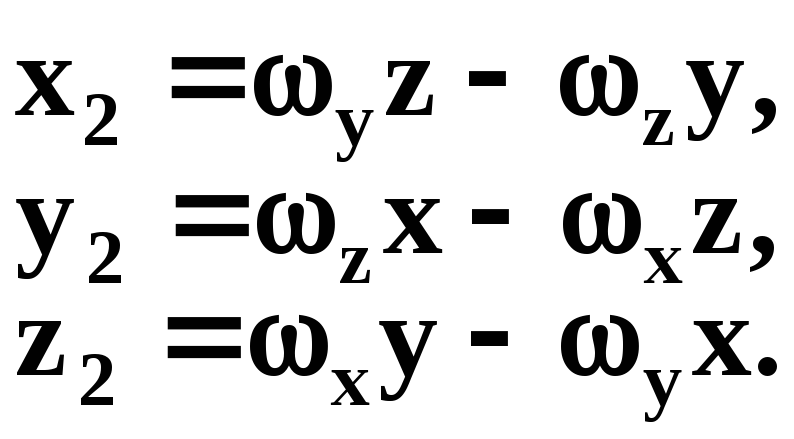(1.10)

Проаналізуємо отримані результати. На підставі (1.8) можна стверджувати, що після деформації положення точки А відносно переміщених разом з точкою 0 вісей x, y, zвизначається деяким векторомз складовими x₁, y₁, z₁ . Цей вектор можна представити у вигляді суми трьох векторів:

(1.11)

Вектор з складовимиx, y, z визначає положення точки А до деформації. Таким чином, під дією прикладених сил точка А відносно вісей x, y, z здійснює два переміщення, які визначаються векторамиз складовими відповіднотаx₂, y₂, z₂.

Враховуючи (1.10), можна записати

(1.12)

Цей запис еквівалентний векторному добутку З останнього виразу слідує, що переміщення точок пружного тіла, яке визначається вектором, відбувається від їх обертання (повороту) навколо вісі, напрямок якої визначається вектором(рисунок 1.2).

Кут повороту чисельно дорівнює величині вектора . Переміщення точки А спрямовано по дотичній до кола, радіус якого показаний на рисунку пунктирною лінією. Векторє нормальним до векторівта.

Таким чином, ми бачимо, що переміщення точок пружного тіла, яке визначається вектором , не супроводжується деформаціями. В цьому випадку тіло обертається навколо деякої вісі та ніякої зміни віддалей між точками тіла не відбувається.

Повертаючись до рівності (1.11), тепер можна зробити висновок, що деформаційне переміщення визначається тільки вектором .

z

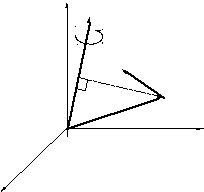
A

0x

y

Рисунок 1.2 - Переміщення точки А пружного тіла, які не супроводжуються деформаціями