3 Зв’язок між напруженнями і

ДЕФОРМАЦІЯМИ

3.1 Експериментальний закон Гука

Між напруженим і деформованим станом, виникаючим в пружному тілі під дією прикладених сил, існує визначений зв’язок. Найбільш простим способом він визначається із дослідів поздовжнього розтягу пружного стержня.

Досліди показують, що у випадку малих деформацій в межах початкової (пружної) дільниці розтягнень між розтягуючою силою , діючою на одиницю площі поперечного перерізу стержня, і відносним видовженням йогоспостерігається пряма пропорційна залежність:

. (3.1)

Коефіцієнт пропорційності називається модулем Юнга і є однією із характеристик пружних властивостей твердого тіла.

Дослід також показує, що поздовжнє видовження стержня при його розтягненні супроводжується поперечним стисненням (зменшенням його діаметру на величину); причому ці деформації пропорційні видовженню:

. (3.2)

Коефіцієнт пропорційності називається коефіцієнтом Пуассона. Він є другою характеристикою пружних властивостей твердого тіла. Іноді використовується величина, обернена до коефіцієнту Пуассона,, яка називається числом Пуассона.

Залежності (3.1) і (3.2) складають закон Гука.

Деформації, що задовольняють закону Гука, - величини малі, порядку однієї-двох тисячних. Наприклад, для матеріалів типу заліза при розтягненні тонкого бруска середня допустима величина напруження – близько 210⁸ Па, а середня величина - близько 210¹¹ Па. Тому з (3.1) отримаємо, що середнє допустиме значення близько однієї тисячної.

Числове значення модуля Юнга для різних гірських порід змінюється в широких границяx. Наприклад, для осадових порід значення модуля змінюється від 0,0310¹⁰ Па (глини) до 16,510¹⁰ Па (доломіти), для кристалічних порід – від 5,6610¹⁰ Па (гнейси) до 12,210¹⁰ Па (габро). Значення коефіцієнта Пуассона змінюється в діапазоні 0,1-0,45. Наближено можна прийняти значення коефіцієнта Пуассона рівним 0,25 для всіх гірських порід.

Теорія пружності, основана на використанні закону Гука, носить назву лінійної теорії пружності.

3.2 Узагальнений закон Гука

Встановимо зв’язок між компонентами напружень і деформації.

Виділимо в пружному тілі елементарний об’єм у вигляді призматичного стержня з ребрами, паралельними трьом головним вісям напружень 1, 2, 3, і центром в точці 0 (рисунок 3.1). Тоді перпендикулярно до граней стержня, тобто вздовж осей 1, 2, 3, будуть діяти головні напруження ,,. Вони будуть зміщувати точки пружного тіла, що лежать на осях 1, 2, 3, вздовж цих осей. Таким чином, осі 1, 2, 3 будуть і головними осями деформації.

Будемо вважати, що деформації стержня малі. В цьому випадку на основі закону Гука можна стверджувати, що деформації його будуть прямо пропорційні напруженням.

Знайдемо видовження стержня вздовж осі 1. Під дією тільки силице видовження, згідно (3.1), буде

,(3.3)

де - довжина стержня вздовж осі1 до прикладення сил; - модуль Юнга пружного тіла.

₃

3

X₁₂₃

'''₁₂₃

₁

''₁₂₃

'₁₂₃

1

Рисунок 3.1 – Деформація стержня під дією напружень

Одночасно з силою вздовж осі 2 діє сила. Ця сила вздовж осі 1 призводить поперечне стиснення, яке можназнайти на основі (3.2):

, (3.4)

де - число Пуассона;- довжина стержня вздовж осі 2 до прикладення сил;- видовження стержня вздовж осі 1.

Поперечне стиснення , під дією силивизначається із співвідношення

. (3.5)

Загальне видовження під дією всіх трьох сил,,на основі (3.3), (3.4) і (3.5) буде

або з врахуванням (1.20)

(3.6)

Аналогічно, розглядаючи загальне подовження вздовж вісей 2 і 3, отримаємо

(3.7)

(3.8)

Позначимо . Тоді вирази (3.6), (3.7) і (3.8) можна записати інакше

(3.9)

Замість модуля Юнга Е та числа Пуасона m часто розглядають, так звані, коефіцієнти Ламе  і  . Вони також характеризують пружні властивості ізотропних тіл.

Просумуємо рівняння системи (3.9). Враховуючи, що

будемо мати

Звідси

Позначимо

(3.10)

(3.11)

З врахуванням (3.10) і (3.11) система (3.9) буде

(3.12)

Перейдемо тепер від системи координат 1, 2, 3 до довільної системи x, y, z. Через    позначимо, спрямовуючи косинуси осей х, y, z в системі 1, 2, 3. Помножимо перше рівняння (3.12) на , друге на, трете ната складемо їх. Тоді на підставі (1.28) і (2.23) отримаємо

(3.13)

Помножимо ті самі рівняння систем (3.12) на ,,, а потім - відповідно на,,. Після додавання на підставі сумування квадратів спрямовуючих косинусів отримаємо

(3.14)

(3.15)

Далі, помножимо перше рівняння (3.12) на , друге на, трете на. Після складання отримаємо

(3.16)

Помножимо те саме рівняння (3.12) на ,,, а потім їх же на,,. Додаючи, в обох випадках, отримаємо

(3.17)

. (3.18)

Розв’яжемо тепер рівняння (3.13), (3.14), (3.15), (3.16), (3.17) і (3.18) відносно компонент напруження. Отримаємо

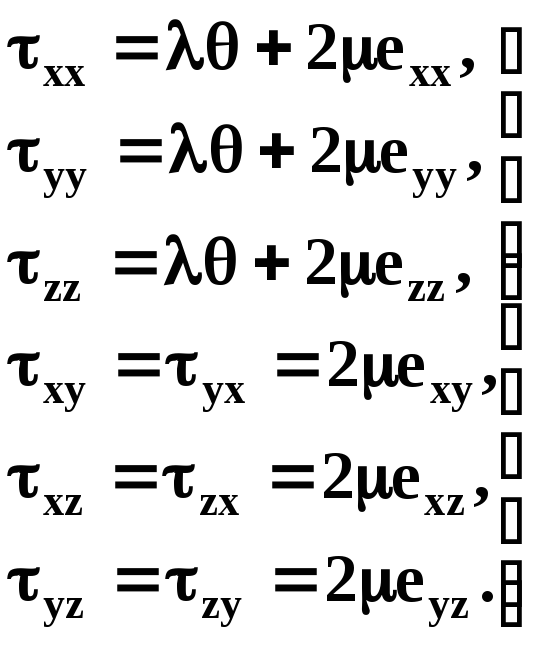(3.19)

Формули (3.19) – це узагальнений закон Гука. Беручи до уваги, що

;

;

Остаточно маємо наступні залежності між компонентами векторів напруження і складовими векторами зміщень:

(3.20)

Це модифікація узагальненого закону Гука в переміщення. Фізичний зміст перших трьох формул полягає у тому, що кожне нормальне напруження характеризує в основному лінійну деформацію в тому ж напрямку. Тому в ці вирази входять деформації Ці деформації будуть супроводжуватися поперечним стиском або розтяганням, що призведе до зміни об’ємуДотичні ж напруження, як випливає з інших трьох формул системи (3.20), характеризують деформації зсуву. Коефіцієнт визначає степінь опору середовища зміні об’єму, а  - степінь опору середовища зміні форми.