11.2. Зведення матриць до жорданової нормальної форми

Теорема 3. Кожна квадратна матриця А порядку з елементами з

поля Р зводиться в полі Р до жорданової нормальної

форми тоді і тільки тоді, якщо всі характеристичні

корені матриці А знаходяться в самому полі Р.

Доведення.

Необхідність.

Якщо матриця А зводиться до жорданової нормальної форми, тобто подібна деякій жордановій матриці , то ці дві матриці володіють одними і тими ж характеристичними коренями, оскільки характеристичні матриці еквівалентні. Характеристичні корені матрицішукаються просто: оскільки визначник матрицідорівнює добутку її елементів, що знаходяться на головній діагоналі, то поліномрозкладається над полем Р на лінійні множники і його коренями служать числа, що знаходяться на головній діагоналі матриці, і тільки вони (а вони є елементами поля Р). Таким чином, характеристичні корені матрицітеж належать Р.

Достатність.

Нехай всі характеристичні корені матриці А знаходяться в полі Р. Якщо інваріантні множники матриці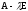(ті, що не дорівнюють 1) будуть, то

.

Дійсно, визначники матриці і її канонічної матриці можуть відрізнятися один від одного тільки сталим множником, який насправді дорівнює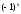, оскільки саме таким є старший коефіцієнт характеристичного полінома. Таким чином,

• серед поліномів немає рівних 0;

• сума степенів цих поліномів рівна ;

• всі вони розкладаються над полем Р на лінійні множники (тому, що за умовою поліном володіє таким розкладом).

Нехай (4) будуть розкладами поліномів в добутки степенів лінійних множників. Назвемоелементарними дільниками полінома відмінні від 1 степені різних лінійних двочленів, які входять в його розклад (4), тобто. Елементарні дільники всіх поліномівназиваютьсяелементарними дільниками матриці А. Випишемо їх у вигляді таблиці (3).

Утворимо тепер жорданову матрицю порядку, складену із жордановим кліток, які визначаються так: кожному елементарному дільникуматриці А ставимо у відповідність жорданову клітку порядку, яка відноситься до числа. Очевидно, що нерівними 1 інваріантними множниками матрицібудуть поліномиі тільки вони. Тому матрицііеквівалентні і, значить, матриця А подібна жордановій матриці. ▲

Приклад

Звести матрицю А до жорданової нормальної форми:

.

Зводячи звичайним способом матрицю до канонічного вигляду, одержимо, що нерівними 1 інваріантними множниками цієї матриці будуть поліномиі. Видно, що матриця А зводиться до жорданової нормальної форми навіть в полі раціональних чисел. Її елементарними дільниками є поліноми, а тому жордановою нормальною формою матриці А є матриця.

Необхідна і достатня умова зведення матриць до діагонального вигляду

На основі отриманих результатів може бути сформульована, нарешті, необхідна і достатня умова звідності матриць до діагонального вигляду.

Теорема 4. Матриця А порядку з елементами з поляР зводиться

до діагонального вигляду тоді і тільки тоді, якщо усі її

характеристичні корені (або всі корені останнього

інваріантного множника її характеристичної

матриці) знаходяться в полі Р, причому серед них нема

кратних.

Доведення.

Дійсно, звідність матриці до діагонального вигляду рівносильна звідності до такого жорданового вигляду, всі жорданові клітки якого мають порядок 1. Іншими словами, всі елементарні дільники матриці А повинні бути поліномами першого степеня. Оскільки, однак, всі інваріантні множники матриці являються дільниками полінома, то остання умова рівносильна тому, що всі елементарні дільники поліномамають степінь 1, що й треба довести. ▲