8.3. Підпростори векторного простору

Підпростором векторного простору V називається сукупність V₁ його елементів, яка сама є векторним простором відносно введених в V операцій додавання і множення на число.

Для встановлення того, що деяка підмножина V₁ векторного простору V є його підпростором, досить показати, що для довільних двох векторів х та у із V₁ їх сума х+у теж належить V₁, і що для довільного вектора і довільногодобутоктеж належитьV₁. Це твердження випливає із аксіом 1, 2, 5-8 векторного простору.

Приклади

Сам простір V і множина із єдиного нульового елемента є підпросторами простору V (тривіальними).

У звичайному тривимірному векторному просторі підпросторами є всі площини і всі прямі, які проходять через початок координат.

Перетином двох підпросторів V₁ і V₂ векторного простору V називається множина всеможливих векторів із V, що належить одночасно V₁ і V₂. Перетин підпросторів теж є підпростором і позначається

Сумою двох підпросторів V₁ і V₂ називається множина векторів вигляду 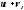деСума підпросторів теж є підпростором і позначаєтьсяV₁+V₂.

Теорема. Якщо V₁ і V₂ – підпростори векторного простору V, то

dimV₁+dimV₂=dimV₁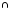V₂+dim(V₁+V₂).

Доведення.

В підпросторі виберемо довільний базисе₁, е₂, …, е_k і доповнимо його до базису V₁ з одного боку:

е₁, е₂, …, е_k, f_k+1, …, f_p (*)

і до базису V₂ з другого боку:

е₁, е₂, …, е_k, g_k+1, …, g_s (**).

Покажемо , що вектори е₁, е₂, …, е_k, f_k+1, …, f_p, g_k+1, …, g_s лінійно незалежні.

Припустимо, що ці вектори лінійно залежні:

Тоді вектор

належить одночасно і V₁, і V₂, а, значить, і їх перетину V₁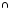V₂. Але тоді він повинен лінійно виражатись через базисні вектори підпростору V₁V₂:

тобто

.

Звідси, а також з єдиності розкладу вектора а за базисом простору V₁ маємо

Тоді матимемо

звідки, із лінійної незалежності базисних векторів простору V₂, маємо

Отже, вектори е₁, е₂, …, е_k, f_k+1, …, f_p, g_k+1, …, g_s утворюють лінійно незалежну систему. Але тоді вони утворюють базис простору V₁+V₂, оскільки, якщо вектор тоz=x+y, де і, значить,х лінійно виражається через (*), а у – через (**). Але тоді вектор z лінійно виражається через вектори

е₁, е₂, …, е_k, f_k+1, …, f_p, g_k+1, …, g_s.

Таким чином, розмірність підпростору V₁+ V₂ дорівнює

k+(p-k)+(s-k)=p+s-k.

Але dimV₁=p, dimV₂=s, dimV₁V₂=k. Тоді

dimV₁+dimV₂=p+s і dimV₁V₂+dim(V₁+V₂)=k+(p+s-k)=p+s,

що й треба довести.

8.4. Лінійні перетворення у векторному просторі

а) Основні поняття

Кажуть, що в лінійному просторі V задано перетворення A, якщо кожному вектору поставлений у відповідність деякий векторA (х) (пишуть Aх). Вектор Aх називають образом вектора х.

Перетворення A називається лінійним, якщо для довільних двох векторів х та у із V і довільного дійсного числа α виконуються рівності:

1. A(х+у)= Aх+Aу,

2. A(αх)=αAх.

Виберемо в просторі V довільний базис е=(е₁, е₂, …, е_п). Тоді деякий вектор в цьому базисі розкладеться так:

х=х₁е₁+х₂е₂+…+х_пе_п,

де х₁, х₂, …, х_п – компоненти вектора х в даному базисі. Оскільки A – перетворення лінійне, то

Aх=A (х₁е₁+х₂е₂+…+х_пе_п)=х₁Aе₁+х₂Aе₂+…+х_пAе_п.

Оскільки Aе_і (і=1, 2, …, п) – теж вектори із V, то їх можна розкласти за вибраним базисом:

Aе₁=а₁₁е₁+а₂₁е₂+…+а_п1е_п,

Aе₂=а₁₂е₁+а₂₂е₂+…+а_п2е_п,

…………………………………

Aе_п=а_1пе₁+а_2пе₂+…+а_ппе_п,

звідки

Aх=х₁(а₁₁е₁+а₂₁е₂+…+а_п1е_п)+х₂(а₁₂е₁+а₂₂е₂+…+а_п2е_п)+…

+х_п(а_1пе₁+а_2пе₂+…+а_ппе_п)=

=(а₁₁х₁+а₁₂х₂+…+а_1пх_п)е₁+(а₂₁х₁+а₂₂х₂+…+а_2пх_п)е₂+…+(а_п1х₁+а_п2х₂+…+а_ппх_п)е_п.

Якщо координатами вектора Aх в базисі е є тобто

,

то із єдиності розкладу вектора за базисом отримаємо:

а₁₁х₁+а₁₂х₂+…+а_1пх_п,

а₂₁х₁+а₂₂х₂+…+а_2пх_п,

………………………………

а_п1х₁+а_п2х₂+…+а_ппх_п.

Звідси випливає, що кожному лінійному перетворенню A в заданому базисі е відповідає цілком певна матриця

А=

стовпчиками якої є коефіцієнти розкладу векторів Aе_і (і=1, 2, …, п) за базисом е і рядками якої є коефіцієнти розкладу вектора Aх за координатами вектора х.

Ясно, що в п-вимірному векторному просторі V кожна квадратна матриця п-го порядку є матрицею деякого лінійного перетворення.

Матрицю A називають матрицею лінійного перетворення. Лінійне перетворення називається виродженим (невиродженим), якщо його матриця вироджена (невироджена).

При невиродженому лінійному перетворенні лінійно незалежні вектори переходять в лінійно незалежні вектори.

Дійсно, якщо вектори е₁, е₂,…, е_k лінійно незалежні і

,

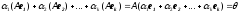то (із невиродженості A)

і α₁=α₂=…=α_k=0 (за умовою).

Отже, вектори Aе₁, Aе₂, …, Aе_k теж лінійно незалежні, що й треба довести. ▲

Приклади

1. Нехай A – поворот всіх векторів площини хОу навколо початку координат на кут φ проти годинникової стрілки. Припустимо, що базисні вектори – одиничні і взаємно ортогональні. Вектор Aе₁ – одиничний, він утворює з е₁ кут φ, з е₂ – кут . Значить,Aе₁=cosφ·е₁+sinφ·e₂. Вектор Aе₂ – теж одиничний, він утворює з е₁ кут зе₂ – φ. Значить, Aе₂=sinφ·e₁+cosφ·e₂. Отже,

А=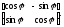

2. Нехай A – ортогональне проектування на площину хОу. Це перетворення лінійне, оскільки проекція суми векторів дорівнює сумі проекцій доданків, проекція добутку вектора на число дорівнює добутку проекції вектора на це число. Якщо в ролі базису вибрано одиничні вектори е₁, е₂, е₃ прямокутної декартової системи координат, то Ае₁=е₁, Ае₂=е₂, Ае₃=θ, і, значить,

А=

3. Нехай ℰ – тотожнє перетворення векторного простору V, яке визначається рівністю ℰх=х для всіх 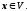Тодіℰе_і=е_і для всіх і=1, 2, …, п, і, значить,

А=

4. Нехай Ơ – так зване нульове перетворення векторного простору V, яке визначається рівністю Ơх=θ для всіх . Матриця цього перетворення є нульовою і

А=

Перетворення 1 і 3 – невироджені, 2 і 4 – вироджені.

б) Операції над лінійними перетвореннями

Сумою двох лінійних перетворень A та ℬ називається таке перетворення A + ℬ, при якому

Властивості:

1. A + ℬ = ℬ + A.

2. (A + ℬ)+ С = A +( ℬ + С).

3. A + Ơ = A.

Добутком лінійного перетворення А на число α називається таке теж лінійне перетворення αA, при якому

Властивості:

1. 1· A = A.

2. α(βA)=(αβ)A.

3. (α+β)A =αA +βA.

4. α(A + ℬ)=αA +αℬ.

Добутком лінійних перетворень A та В називається таке теж лінійне перетворення AВ, при якому

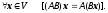
Властивості:

1. (A ℬ)С =A (ℬС).

2. Aℰ=A.

3. (A+ ℬ)С =AС + ℬС.

4. С(A + ℬ)= С A + С ℬ.

Для кожного невиродженого лінійного перетворення A існує таке (обернене до A) лінійне перетворення A^-1, що A∙A^-1=A^-1·A=ℰ.

Ясно, що добуток невироджених лінійних перетворень теж є невиродженим лінійним перетворенням.

в) Перехід до нового базису

Нехай лінійне перетворення A в базисі е=(е₁, е₂, …, е_п) має матрицю А, а в базисі - матрицю А'. Знайдемо зв’язок між ними.

Позначимо через С матрицю переходу від базису е до базису . Тоді

Будемо матрицю С розглядати як матрицю лінійного перетворення С в базисі е. Тоді

Значить, лінійне перетворення С переводить вектори базису е у вектори базису . Відомо, що визначник матриці С відмінний від нуля, значить, дляС існує обернене перетворення С^-1, при якому

За умовою,

.

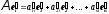Застосуємо до обох частин цієї рівності перетворення С ^-1:

.

Підставимо в ліву частину :

,

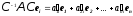тобто матрицею перетворення в базисіе є матриця А' Але, з другого боку матриця цього перетворення рівна добутку матриць відповідних перетворень в базисі е, тобто А'=С^-1АС.

Ясно, що визначник матриці лінійного перетворення не залежить від базису:

Приклад

В базисі е₁, е₂ перетворення A має матрицю A=

Написати матрицю цього перетворення в базисі

Матриця переходу С= Тоді С^-1= Звідси

А'=

г) Ранг і дефект лінійного перетворення

Сукупність всеможливих векторів вигляду Aх, де , називаєтьсяобластю значень або образом лінійного перетворення А. Позначається ImA.

Сукупність всеможливих векторів , для якихAх=θ, називається ядром лінійного перетворення A. Позначається Ker A.

І образ, і ядро лінійного перетворення A є підпростором в V.

а) Якщо ImA, то х=Aх₁, у=Aу₁, де тох+у=Aх₁+ Aу₁= A(х₁+у₁), де і, значить,ImA.

αх=αAх₁=A (αх₁), де і, значить,I mA.

Отже, ImA – підпростір простору V.

б) Якщо KerA, тобто якщо Aх=θ і Aу=θ, то і

A(х+у)= Aх+Aу=θ+θ=θ і

A(αх)= αAх=α·θ=θ,

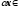тобто х+уKerA і KerA.

Отже, KerA – підпростір простору V.

Розмірність образу перетворення A dim(ImA) співпадає з рангом матриці А цього перетворення і називається рангом перетворення A. Дійсно, підпростір ImA породжується векторами Aе₁, Aе₂, ..., Aе_п, де е={e₁, e₂, …, e_n} – довільний базис простору V і, значить, розмірність ImA дорівнює максимальній кількості лінійно незалежних стовпчиків матриці А.

Розмірність ядра dim(KerA) називається дефектом лінійного перетворення A.

Важливим є твердження, що сума рангу і дефекту лінійного перетворення A дорівнює розмірності п простору V. Тобто,

dim(ImA)+dim(KerA)=n.