7.3. Матрична форма запису системи лінійних рівнянь

Для системи m лінійних рівнянь з п невідомими

вводяться наступні позначення:

А=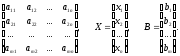

Тоді система лінійних рівнянь запишеться у вигляді матричного рівняння АХ=В. Цю форму запису системи лінійних рівнянь називають матричною формою. Нехай кількість рівнянь m у системі дорівнює кількості невідомих п, причому визначник |А| цієї системи відмінний від нуля. Якщо записане матричне рівняння має розв’язок Х^*= тобто виконується рівність АХ^*=В, то, помноживши зліва обидві частини рівності на А^-1, матимемо А^-1АХ^*=А^-1В, звідки Х^*=А^-1В, тобто отримаємо матричний вигляд розв’язку заданої системи лінійних рівнянь.

Отже, якщо вихідне матричне рівняння із невиродженою матрицею А має розв’язок, то він єдиний і задається формулою

Х^*=А^-1В.

Приклад

Розв’язати систему лінійних рівнянь матричним способом

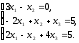
А А^-1

Х^*=А^-1В=

Отже, розв’язок (3;9;2).

Лекція 8. Векторні простори

8.1. Поняття векторного простору, його розмірність і базис

а) Означення

Множина V елементів x, y, z, … називається лінійним, або векторним, простором, якщо сума х+у довільних двох її елементів х, у і добуток αх кожного її елемента х на будь-яке число α теж належать множині V, причому виконуються наступні умови:

1. 

2. 

3. θ називають нульовим елементом простору.

4. –х називають елементом, протилежним до х.

5. 1·х=х.

6. 

7. 

8. 

Елементи векторного простору називають векторами.

Приклади векторних просторів

1. Множина розв’язків системи лінійних однорідних рівнянь.

2. Множина всеможливих рядків чи стовпчиків, які містять п дійсних чисел.

3. Множина поліномів не вище п-го степеня з дійсними коефіцієнтами.

Якщо в просторі V визначено множення його елементів на дійсні (комплексні) числа, то V називають дійсним (комплексним) векторним простором.

Із означення векторного простору випливають наступні властивості.

1. Єдиність нуля.

Якщо припустити існування двох нульових елементів θ₁ і θ₂, то із θ₁+ θ₂= θ₁ та θ₂+ θ₁= θ₂ і того, що θ₁+ θ₂= θ₂+ θ₁, випливає θ₁= θ₂.

2. Єдиність протилежного елемента.

Якщо припустити існування двох протилежних до х елементів y та z, таких, що х+у=θ і х+z=θ, то із

y+x+z=y+(x+z)=y+θ =y та

y+x+z=(y+x)+z=θ+z=z

випливає y=z.

3. 0∙х=θ.

Дійсно, 0∙х=(0+0)∙х=0∙х+0∙х. Додавши до обох частин рівності -0∙х отримаємо θ=0∙х.

4. 

Дійсно, Додавши до обох частин рівностіотримаємо

5. Якщо добуток αх=θ, то або α=0, або х=θ.

Дійсно, якщо то

6. є протилежним до х.

Дійсно, х+(-1)х=1·х+(-1)х=[1+(-1)]x=0·x=θ, звідки (-1)х= -х.

б) Розмірність і базис

Вектори а₁, а₂, …, а_k векторного простору V називаються лінійно залежними, якщо існують такі числа одночасно не рівні нулю, що

В іншому випадку вектори називають лінійно незалежними.

Якщо вектори а₁,а₂,…,а_k лінійно залежні, тобто , і, наприклад,то

тобто

де

Це означає, що вектор а_k є лінійною комбінацією решти векторів системи. Отже, якщо вектори а₁, а₂,…,а_k лінійно залежні, то, принаймні, один із них лінійно виражається через решту. Ясно, що справедливе і зворотнє твердження.

Максимальна кількість лінійно незалежних векторів системи векторів а₁, а₂, …, а_k називається рангом цієї системи. Позначають rank {а₁, а₂, …, а_k}.

Довільна матриця А=містить дві системи векторів:

систему векторів-рядків і систему векторів-стовпчиків,

де , і=1, 2, …, m, ,j=1, 2, …, n.

Ранг системи рядків довільної матриці А дорівнює рангу її стовпчиків і називається рангом матриці А. Позначається rank А або r(A).

Таким чином, для знаходження рангу матриці досить з допомогою елементарних перетворень над рядками (стовпчиками) звести її до східчастого вигляду і підрахувати кількість ненульових рядків (стовпчиків), яка й дорівнюватиме кількості лінійно незалежних серед них, а, отже, рангу матриці.

Приклад

Знайти ранг матриці

А=.

Зведемо матрицю А до східчастого вигляду з допомогою елементарних перетворень її рядків:

Отже, r(A)=3.

Розмірністю векторного простору V називається максимальна кількість лінійно незалежних векторів, що містяться в ньому. Позначається dimV (від dimage – фр).

Приклади

1. Розмірність множини всіх векторів площини дорівнює два.

2. Розмірність множини просторових векторів – три.

Простори із скінченною розмірністю називаються скінченновимірними.

Базисом простору V називають впорядковану скінченну систему векторів, якщо:

1. вона лінійно незалежна;

2. кожний вектор простору V є лінійною комбінацією векторів цієї системи.

Коефіцієнти заданої лінійної комбінації називаються компонентами або координатами вектора за цим базисом.

Компоненти вектора у вибраному базисі визначаються однозначно.

Дійсно, при двох заданнях вектора х в базисі а₁, а₂, …, а_k, зокрема, та, отримаємо. Оскільки система а₁, а₂, …, а_k лінійно незалежна, то всі коефіцієнти , звідки

В п-вимірному просторі кожна впорядкована лінійно незалежна система із п лінійно незалежних векторів є базисом. Ясно, що в п-вимірному просторі кожну впорядковану лінійно незалежну систему із k<n векторів можна доповнити до базису.

Розглянемо в просторі V два базиси: е=(е₁,е₂,…,е_п) та е' (перший з них назвемо старим, а другий – новим). Виразимо кожний вектор нового базису через вектори старого базису:

Можна сказати, що нові базисні вектори виражаються через старі з допомогою матриці

А

стовпчиками якої є коефіцієнти їх розкладу за векторами старого базису. Матриця А називається матрицею переходу від базису е до базису е'. Матриця переходу є невиродженою, оскільки в іншому випадку її стовпчики, а, отже, і вектори , були б лінійно залежними.

Розглянемо зв’язок між координатами одного і того ж вектора в старому і новому базисах.

Нехай х=х₁е₁+х₂е₂+…+х_пе_п і

Підставивши замість їх вирази черезе₁, е₂, …, е_п, отримаємо

Із єдиності розкладу вектора х за базисом е₁, е₂, …, е_п, випливає

звідки .

Таким чином, старі координати вектора отримуються із нових з допомогою тієї ж матриці А, тільки коефіцієнти відповідних розкладів утворюють рядки цієї матриці.

Приклад

Нехай е₁, е₂ – одиничні вектори, розташовані вздовж осей прямокутної декартової системи координат. Повернемо осі координат на кут φ проти годинникової стрілки і позначимо нові базисні вектори через та. Кути, утворені векторомз векторамие₁ і е₂, рівні відповідно φ і 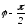(малюнок). Тому координати цього вектора в базисі е₁, е₂ рівні ізначить,. Аналогічно, кути вектораз векторамие₁ і е₂ рівні відповідно 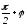іφ, тому координати його в базисі е₁, е₂ рівні і, значить,

e₂

φ φ

e₁

Таким чином, матриця переходу від базису е₁, е₂ до базису ,матиме вигляд

А=

Тоді старі координати виражаються через нові так:

звідки