6.4. Обчислення визначників n-го порядку

В пункті 6.2 отримано формулу, яка дає можливість обчислення визначника n-го порядку:

А =|А|=,

де M_ij – мінор матриці, який відповідає елементові a_ij (j=1, 2, …, n). Добуток (-1)^i+jM_ij називають алгебраїчним доповненням елемента а_ij у визначнику |А| і позначають А_ij .

Теорема 6.1. Визначник матриці А дорівнює сумі добутків усіх

елементів будь-якого його рядка на їх алгебраїчні

доповнення.

А =|А|=.

Доведення.

При і=1 твердження справедливе:

.

Замінивши тепер кожен добуток на А_1j, отримаємо:

А =|А|=.

Нехай і>2 . Переставляючи послідовно і-й рядок визначника з кожним, що стоїть над ним, черезі-1 переставлянь отримаємо визначник:

.

(згідно власт. 2), звідки .

Застосуємо до визначника відоме означення, отримаємо

.

Підставимо це значення в А:

А =, тобто

Оскільки , то

А =.

Із того, що , випливає

А =,

що й треба довести. ▲

Оскільки рядки і стовпчики визначника рівноправні, то аналогічний розклад можливий і за елементами довільного стовпчика.

Теорема 6.2. Сума добутків всіх елементів деякого рядка

визначника А на алгебраїчні доповнення відповідних

елементів іншого рядка дорівнює нулю:

Доведення.

Розкладемо визначник за елементами s-го рядка:

А =

Алгебраїчні доповнення А_sj (j=1, 2, ..., n) не залежать від елементів а_sj, тому остання рівність буде справедливою при будь-яких значеннях елементів а_sj , зокрема й при а_sj = а_ij (тобто, коли на місці елементів s-го рядка знаходитимуться елементи і-го рядка). Але при а_sj=а_ij визначник А матиме два однакові рядки і тому дорівнюватиме нулю. Тому

,

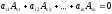що й треба довести. ▲

Ясно, що аналогічний висновок має місце і для розкладу за елементами довільного стовпчика.

Приклад

Обчислити визначник, розклавши його за елементами 3 рядка:

Чим більше елементів у рядку (чи стовпчику) визначника дорівнюють нулю, тим простішим є розклад визначника за елементами цього рядка. Ясно, що найпростішим є варіант, коли деякий рядок (стовпчик) містить тільки один ненульовий елемент. Цього можна добитися з допомогою виконання над рядками (стовпчиками) визначника відповідних елементарних перетворень. Зокрема, в деякому j-тому стовпчику можна отримати нуль в деякому і-му рядку, якщо відняти від і-го рядка, наприклад, перший рядок, помножений на , чи другий рядок, помножений наі т. д.

Приклад

Обчислити визначник: .

Виберемо 4^й стовпчик:

Виберемо 4^й рядок:

Лекція 7. Системи лінійних рівнянь

7.1. Загальні поняття

Рівняння з n невідомими називається лінійним, якщо його можна подати у вигляді:

,

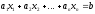де – коефіцієнти,b – вільний член рівняння (дійсні числа).

Сукупність записаних в певному порядку чисел називаєтьсярозв’язком рівняння, якщо після заміни в ньому невідомих х_і відповідними числами (і=1,2,…,п), воно перетворюється в правильну рівність.

Розглянемо систему m лінійних рівнянь з п невідомими:

Розв’язком системи лінійних рівнянь називається така сукупність записаних у певному порядку чисел , що кожне з рівнянь системи перетворюється на правильну рівність після заміни в ньому невідомихх_і відповідними числами (і=1, 2, …, п).

Система лінійних рівнянь, яка має розв’язки, називається сумісною. Система, яка не має жодного розв’язку, називається несумісною.

Сумісна система лінійних рівнянь називається визначеною, якщо вона має тільки один розв’язок, і невизначеною, якщо кількість її розв’язків більша одного.

Системи лінійних рівнянь називаються еквівалентними, якщо множини їх розв’язків збігаються.

Кожне елементарне перетворення системи лінійних рівнянь переводить її в еквівалентну систему.

Лінійне рівняння називається неоднорідним, якщо його вільний член не дорівнює нулю, і однорідним, якщо вільний член дорівнює нулю.

Аналогічно, система лінійних рівнянь називається однорідною, якщо всі її рівняння однорідні.