6.3. Властивості визначника n-го порядку

Перетворення матриці, при якому її рядки стають стовпчиками з тими ж номерами, називається транспонуванням цієї матриці. Транспонованою щодо даної матриці А є матриця

А'

Транспонуванням квадратної матриці є, по суті, її поворот навколо діагоналі на кут 180º.

Властивість 1. Визначник не змінюється при транспонуванні.

Згідно означення, визначник матриці А дорівнює алгебраїчний сумі n! членів вигляду , де індекси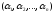 утворюють деяку перестановку із чисел 1, 2, …, n. Нехай 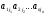є довільно вибраним членом визначника матриці А. Однак всі множники цього добутку є і елементами матриці А' і містяться в різних його стовпчиках і різних рядках. Тому цей довільний добуток є членом і визначника А'. Оскільки знак цього члена у визначнику |А| визначається парністю підстановки, а у визначнику |А'|– парністю підстановки, які мають однакову парність, то в обох визначниках цей член береться з однаковим знаком.

Отже, обидва визначники |А| та |А'| є сумами одних і тих самих членів, взятих з однаковими знаками, тобто є рівними. ▲

Властивість 2. Якщо у визначнику поміняти місцями довільні два рядки, то визначник тільки змінить знак на протилежний.

Нехай у визначнику |А| помінялись місцями k-й та l-й рядки. Знак довільного члена визначника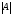визначається парністю підстановки

,

а у новому визначнику – підстановки

,

яка має протилежну парність із-за наявності транспозиції (l,k). Отже, кожний довільний член входить до обох визначників з протилежними знаками. Оскільки обидва визначники складаються з одних і тих же членів, що входять до них з протилежними знаками, то від переставлення місцями двох рядків визначник тільки змінить знак. ▲

Властивість 3. Якщо всі елементи одного з рядків визначника

помножити на деяке число λ, то визначник

помножиться на λ.

Нехай всі елементи і-го рядка визначника помножено на число λ. Оскільки до кожного члена визначника входить співмножником один елемент з і-го рядка, то в кожному члені з’явиться множник λ, тобто визначник помножиться на λ.

Доведена властивість може бути сформульована інакше:

спільний множник всіх елементів довільного рядка визначника можна винести за знак визначника.

Властивість 4. Якщо кожен елемент і-го рядка визначника є сумою

двох доданків a_ij=b_ij+c_ij, (j=1, 2, …, n), то визначник

дорівнює сумі двох визначників, в яких всі рядки, крім

і-го, такі самі, як і в даного визначника, а і-й рядок в

першому визначнику складається з елементів b_ij, а в

другому – c_ij.

▲

Ясно, що властивість 4 можна поширити на випадок, коли кожен елемент і-го рядка є сумою довільної кількості доданків.

Властивість 5. Визначник, який містить хоча б один нульовий

рядок, дорівнює нулю.

Дійсно, якщо всі елементи деякого і-го рядка є нулями, то, оскільки один із цих елементів обов’язково увійде співмножником до кожного члена визначника, всі члени визначника, а, значить, і сам визначник дорівнюватиме нулю. ▲

Властивість 6. Визначник, що містить два однакові рядки, дорівнює

нулю.

Дійсно, помінявши місцями обидва однакові рядки визначника |А|, отримаємо (за власт. 2) визначник -|А|. Оскільки помінялись місцями однакові рядки, то насправді визначник |А| не змінився. Отже, |А|= -|А|, тобто 2|А|=0, звідки |А|=0. ▲

Властивість 7. Визначник, що містить два пропорційні рядки,

дорівнює нулю.

Нехай l-й рядок є добутком k-го рядка на число λ (тобто ці рядки пропорційні). Винесемо з l-го рядка λ і отримаємо визначник з двома однаковими рядками, який дорівнює нулю. ▲

Властивість 8. Визначник, що містить рядок, який є лінійною

комбінацією інших його рядків, дорівнює нулю.

Якщо і-й рядок визначника |А| є лінійною комбінацією m інших його рядків (2<n), то кожен елемент і-го рядка є сумою m доданків, тому визначник дорівнює сумі m визначників, в кожного з яких і-й рядок буде пропорційний одному з інших його рядків. Всі ці визначники дорівнюють нулю, а тому нулю дорівнює і |А|. ▲

Властивість 9. Якщо до одного з рядків визначника додати інший

його рядок, помножений на деяке число λ, то

визначник не зміниться.

Якщо до і-го рядка визначника |А| додати s-й його рядок (s≠i), помножений на деяке число λ, то кожен елемент і-го рядка в новому визначнику буде мати вигляд: 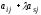(j=1, 2, .., n), тому новий визначник дорівнює сумі двох визначників, перший з яких є |А|, а другий дорівнює нулю як такий, що містить пропорційні і-й та s-й рядки. ▲

Ясно, що визначник не зміниться, якщо до одного з його рядків додати довільну лінійну комбінацію інших його рядків.