
- •Множини
- •Відображення
- •1.3. Бінарні відношення на множині
- •2.1. Принцип математичної індукції Аксіома математичної індукції
- •Узагальнення другої форми принципу математичної індукції
- •2.2. Підстановки
- •Основні алгебраїчні структури
- •3.1. Означення комплексного числа
- •3.2. Дії над комплексними числами
- •3.3. Піднесення до степеня і добування кореня
- •4.1. Поліноми від однієї змінної
- •Г) Найбільший спільний дільник
- •Д) Найменше спільне кратне
- •4.3.Поліноми над числовими полями
- •4.4. Поліноми від багатьох змінних
- •Б) Симетричні поліноми
- •5.1. Поняття матриці
- •5.2. Дії над матрицями
- •6.1. Визначники малих порядків
- •6.2. Поняття визначника n-го порядку
- •6.3. Властивості визначника n-го порядку
- •6.4. Обчислення визначників n-го порядку
- •7.1. Загальні поняття
- •7.2. Способи розв’язування систем лінійних рівнянь
- •7.3. Матрична форма запису системи лінійних рівнянь
- •8.1. Поняття векторного простору, його розмірність і базис
- •8.3. Підпростори векторного простору
- •8.4. Лінійні перетворення у векторному просторі
- •8.5. Власні вектори і власні значення лінійного перетворення а) Інваріантні підпростори
- •Звідси із лінійної незалежності векторів e1, e2, …, en випливає:
- •9.1. Поняття евклідового простору
- •9.2. Ортонормований базис
- •9.3. Лінійні перетворення в евклідовому просторі
- •Властивості:
- •10.1. Лінійна функція (форма)
- •10.2. Поняття білінійної та квадратичної функції
- •10.3. Зведення квадратичної форми до суми квадратів
- •10.4. Закон інерції квадратичних форм
- •10.5. Класифікація квадратичних форм
- •10.6. Білінійні і квадратичні форми в евклідовому просторі
- •10.7. Зведення рівняння другого порядку до канонічного вигляду
- •Виконаємо лінійне перетворення
- •11.2. Зведення матриць до жорданової нормальної форми
- •Необхідна і достатня умова зведення матриць до діагонального вигляду
Частина 1. АЛГЕБРА
Лекція 1. Множини. Відображення. Відношення
Множини
а) Означення множини. Операції над множинами
Множину
визначають як довільну сукупність
об’єктів, які називають елементами
цієї множини. Позначають множини великими
латинськими буквами, а елементи множин
– малими буквами. Той факт, що а
є елементом множини А,
або а
належить множині А,
записують як
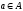 ,
а його заперечення позначається
,
а його заперечення позначається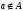 .
Якщо множина задається перерахуванням
її елементів, то вони записуються в
фігурних дужках. Наприклад,
.
Якщо множина задається перерахуванням
її елементів, то вони записуються в
фігурних дужках. Наприклад,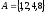 – множина степенів числа 2, що знаходяться
в першій десятці натуральних чисел. Для
означення множиниА
можна скористатись властивістю, яку
мають тільки елементи з А,
наприклад,
– множина степенів числа 2, що знаходяться
в першій десятці натуральних чисел. Для
означення множиниА
можна скористатись властивістю, яку
мають тільки елементи з А,
наприклад,
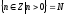 – множина натуральних чисел.
– множина натуральних чисел.
Множину
В
називають підмножиною
множини А,
якщо кожен елемент множини В
є елементом множини А
(В
міститься в А).
Позначають
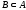 .
Символічний запис:
.
Символічний запис: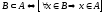 .
.
Однією
із підмножин довільної множини є
порожня
множина
ø, яка зовсім не містить елементів. Для
довільної множини А
сама множина А
і порожня множина називають невласними
підмножинами, всі решта підмножини
називають власними.
Так, множина із двох елементів
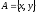 має чотири підмножини: невласні –
має чотири підмножини: невласні –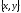 і ø та власні –
і ø та власні –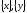 .
.
Дві множини А та В співпадають (або рівні), якщо вони складаються із одних і тих же елементів. Символічний запис:
 або
або
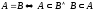 .
.
Об’єднанням двох множин А та В називають множину, що складається із
всіх елементів, які належать хоча б одній із цих множин. Символічний запис:
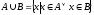 .
.
Перетином двох множин А та В називають множину, що складається із всіх елементів, які належать обом множинам. Символічний запис:
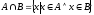 .
.
Різницею двох множин А та В називається множина, що складається із всіх елементів, які належать першій із них і не належать другій. Символічний запис:
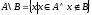 .
.
При
умові
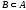 різниця множин
різниця множин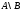 називаєтьсядоповненням
множини В
до множини А.
Позначають доповнення В
до А
через
називаєтьсядоповненням
множини В
до множини А.
Позначають доповнення В
до А
через
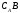 (С
– перша буква французького слова
“complement”
–
доповнення).
(С
– перша буква французького слова
“complement”
–
доповнення).
Об’єднання
різниць
 та
та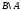 називаютьсиметричною
різницею.
Символічний запис:
називаютьсиметричною
різницею.
Символічний запис:
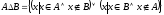 або
або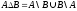 .
.
Якщо
в певній задачі розглядаються підмножини
деякої множини U,
то її називають універсальною
для цієї задачі. Доповнення її підмножини
А
до універсальної множини U
називають просто доповненням і позначають
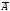 .
.
Наочну картину про найпростіші властивості множин дає схематичне зображення їх у вигляді кіл, і такі схеми називають діаграмами Ейлера-Венна. Універсальну множину зображають прямокутником.
Приклади

Заштрихована
множина –
об’єднання
множин А
та В,
тобто
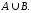
Заштрихована
множина –
перетин
множин А
та В,
тобто

Заштрихована
множина –
різниця
множин А
та В,
тобто
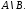
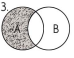
Заштрихована
множина –
доповнення
множини В
до множини А,
тобто
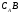 .
.
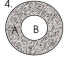
Заштрихована
множина –
симетрична
різниця
множин А
та В,
тобто
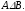
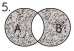
Заштрихована
множина –
доповнення підмножини А до універсальної
множини U,
тобто
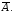


б) Основні властивості операцій над множинами
Властивості об’єднання і перетину
1.
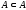 .
.
2.
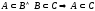 .
.
3.
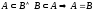 .
.
4.
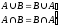 комутативність об’єднання і перетину
(commutatius
– переставний
(лат.)).
комутативність об’єднання і перетину
(commutatius
– переставний
(лат.)).
5.
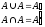 ідемпотентність об’єднання і перетину
(idem
– той самий, potenti
– здатний (лат.)).
ідемпотентність об’єднання і перетину
(idem
– той самий, potenti
– здатний (лат.)).
6.
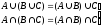 асоціативність об’єднання і перетину
(аssotiatіo
– сполучення (лат.)).
асоціативність об’єднання і перетину
(аssotiatіo
– сполучення (лат.)).
7.
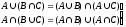 дистрибутивність об’єднання відносно
перетину та перетину відносно об’єднання.
дистрибутивність об’єднання відносно
перетину та перетину відносно об’єднання.
Доведемо для прикладу останню властивість.
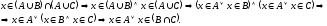
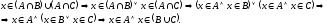
Властивості різниці множин
1.
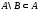 .
.
2.
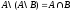 .
.
3.
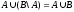 .
.
4.
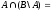 ø.
ø.
5.
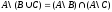 .
.
6.
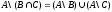 .
.
Властивості доповнень множин
1.
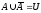 .
.
2.
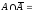 ø.
ø.
3.
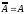 .
.
4.
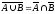 .
.
5.
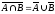 .
.
Властивості порожньої множини
1.
ø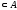 .
.
2.
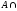 ø
= ø.
ø
= ø.
3.
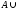 ø
=А.
ø
=А.
4.
ø
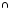 ø
= ø.
ø
= ø.
5.
ø
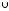 ø
= ø.
ø
= ø.
в) Прямий (декартів) добуток множин
Нехай
А
та В
– довільні множини. Пару (а,b)
елементів
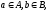 взятих в даному порядку, називаютьвпорядкованою
парою.
Дві впорядковані пари
взятих в даному порядку, називаютьвпорядкованою
парою.
Дві впорядковані пари
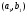 та
та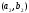 рівні тоді і тільки тоді, коли рівними
є їх відповідні елементи, тобто
рівні тоді і тільки тоді, коли рівними
є їх відповідні елементи, тобто
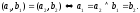
Прямим
або декартовим
добутком
множин А
та В
називається множина всіх упорядкованих
пар (а,b)
елементів, із яких перший належить
першій множині А,
а другий – другій множині В.
Символічний запис:
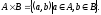
Приклад
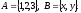
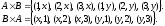
Очевидно,
що операція декартового множення є
некомутативною. Множину
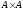 називають декартовим квадратом і
позначають
називають декартовим квадратом і
позначають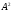 ,
,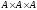 – декартовим кубом
– декартовим кубом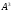 і т.д.
і т.д.
Прямим
або декартовим
добутком
множин
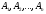 називається множина всіх упорядкованих
сукупностейп
елементів, із яких перший належить
першій множині
називається множина всіх упорядкованих
сукупностейп
елементів, із яких перший належить
першій множині
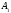 ,
другий – другій
,
другий – другій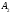 ,
і т.д., останній –
,
і т.д., останній –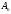 .
.
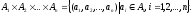
Якщо
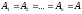 ,
то матимемо
,
то матимемо
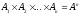
– п-ий
декартів степінь множини А.
Елементами
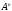 є рядки довжиноюп.
є рядки довжиноюп.
Приклад
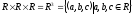
– множина всеможливих точок дійсного тривимірного простору (декартів куб).
