
Курс теоретичної механіки 2007 (Укр)
.pdf
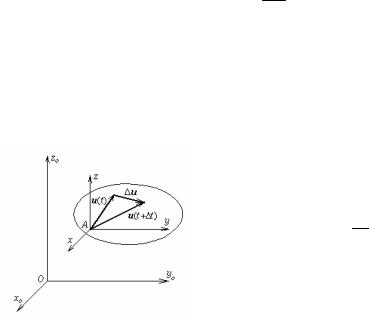
Вектор MM / з'єднує два положення точки відносно нерухомої системи координат, тому ми будемо називати його вектором
абсолютного переміщення. Вектор µ/ ν з'єднує два положення точки,
що рухається, відносно рухливого середовища, тому ми його будемо називати вектором відносного переміщення. Розділивши (58) на t, будемо мати
|
|
|
|
|
|
|
|
|
Va,cp |
= Vr,cp +Vµ,cp |
(59) |
||||
Тут |
Va,cp |
= |
MM / |
|
- |
середня |
абсолютна швидкість |
точки М за |
|||||||
|
|
||||||||||||||
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проміжок |
часу |
|
t, |
Vr,cp |
= |
µ / ν |
- |
середня відносна |
швидкість, а |
||||||
|
t |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vµ,cp |
= |
µµ/ |
|
|
- середня швидкість точки µ за той же проміжок часу. |
||||||||||
|
t |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переходячи в (59) до границі при |
t → 0 і використовуючи рівність |
||||||||||||||
V = lim Vcp , одержуємо |
|
|
|
|
|
|
|||||||||
|
t→0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Va |
= Vr |
|
+Vµ , |
(60) |
||
де Vµ - швидкість точки µ рухливого середовища, з яким збігається точка М в момент часу t. По визначенню швидкість цієї точки і є переносною швидкістю точки М. Тому (60) тотожно (57).
Теорема доведена.
§ 3. Теорема про додавання прискорень (теорема Коріоліса)
Нехай деякий перемінний вектор (вектор-функція) и =и(t) заданий у рухливій системі відліку. Унаслідок руху рухливої системи відліку відносно нерухомої цей вектор буде мати, узагалі говорячи, інше аналітичне вираження в нерухомій системі відліку, а виходить, і його похідні в рухливій і нерухомій системах відліку, узагалі говорячи, теж будуть різними.
Похідну перемінного вектора в нерухомій системі відліку
будемо називати абсолютною і позначати символом da u . dt
81
Похідну перемінного вектора в рухливій системі відліку будемо
називати відносною і позначати символом dr u . dt
Лема 1 (про зв'язок між абсолютною і відносною похідними перемінного вектора). Абсолютна похідна перемінного вектора
дорівнює відносної похідної цього вектора, складеній з векторним добутком кутової швидкості рухливого середовища на цей вектор, тобто
da u |
= |
dr u |
+[ω |
|
, u] . |
(61) |
|
|
e |
||||
dt |
|
dt |
|
|
||
|
|
|
|
|||
Доказ. Нехай рухлива система відліку робить поступальний рух відносно нерухомої. Тоді збільшення и вектора и в обох системах відліку будуть однаковими, а виходить, будуть
однаковими і відносини u і їхні t
границі при t → 0. Це значить,
|
при поступальному переносному |
|||||
|
русі абсолютна і відносна похідні |
|||||
|
перемінного вектора збігаються, |
|||||
|
тобто |
|
|
|
|
|
Мал.24 |
|
da u |
= |
dr u |
. |
(62) |
|
|
|
||||
|
|
dt |
|
dt |
|
|
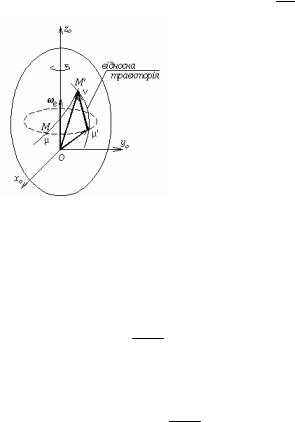
Нехай тепер рухливе середовище обертається навколо нерухомої осі. Направимо осі zо і z нерухомої і рухливої систем відліку уздовж цієї осі (мал.25). Рух точки М, положення якої в кожен момент часу визначається радіусом-вектором и, будемо розглядати як складне. Запишемо для неї теорему про додавання швидкостей:
Va = Vr +Ve . |
(63) |
Вектор и є радіусом-вектором точки М, тому
V |
|
= |
da u |
, V |
|
= |
dr u |
. |
(64) |
a |
|
r |
|
||||||
|
|
dt |
|
|
dt |
|
|||
|
|
|
|
|
|
|
|||
Переносна швидкість точки М дорівнює швидкості точки µ рухливого середовища, що визначається по першій формулі Эйлера (52):
V = [ωе, u]. |
(65) |
82

Підставляючи (64) і (65) у (63), одержуємо
da u = dr u +[ωe , u] .
dt dt
Помітимо, що ця формула містить у собі (62) як окремий випадок, якщо покласти ω=0 при поступальному русі.
Таким чином, лема доведена.
Мал.25
Лема 2 (про абсолютну похідну переносної швидкості).
Абсолютна похідна переносної швидкості точки за часом дорівнює переносному прискоренню, геометрично складеному з векторним добутком кутової швидкості рухливого середовища на відносну швидкість точки, тобто
daVe |
= a |
|
+[ω |
|
,V |
|
] |
(66) |
|
e |
e |
r |
|||||
dt |
|
|
|
|
||||
|
|
|
|
|
|
|
||
Доказ. З визначення похідної вектора-функції випливає
d |
V |
e |
|
V |
e |
(t + t) −V |
e |
(t) |
|
Vν −Vµ |
|
a |
|
= lim |
|
|
|
= lim |
|
(67) |
|||
|
|
|
|
|
|
|
|
|
|||
dt |
|
t→0 |
|
|
t |
|
|
t→0 |
t |
|
|
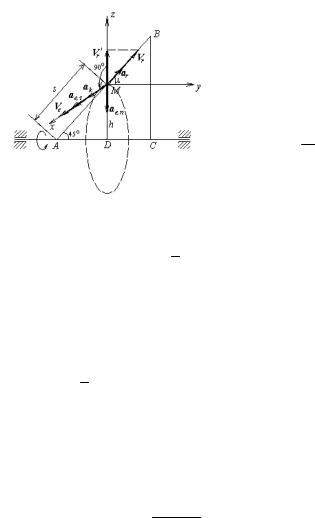
Тут µ – точка рухливого середовища, з яким збігається точка М в момент часу t, а ν – точка цього середовища, з яким точка М збігається в момент часу t+ t (мал.26). Віднімемо і додамо в чисельнику правої частини (67) Vµ' = Vµ (t + t) (µ/ – положення точки µ у момент часу
t+ t): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
a |
V |
e |
|
|
Vν −Vµ' |
|
Vµ |
(t + t) −Vµ (t) |
|
|
||||||||
|
|
|
= lim |
|
|
|
+ lim |
|
|
|
|
|
|
. |
(68) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
dt |
|
|
|
t→0 |
|
t |
|
t→0 |
|
|
|
t |
|
|
||||
Для перетворення першого доданка в правій частині (68) |
||||||||||||||||||||
використовуємо першу формулу Эйлера: |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Vν −Vµ' =[ωe , |
|
|
] – [ωe , Oµ/ ] = [ωe , |
|
|
− Oµ / ] = [ωe , |
µ/ ν ]. (69) |
|||||||||||||
Oν |
Oν |
|||||||||||||||||||
Вектор µ/ ν з'єднує два положення точки М на відносній траєкторії − у моменти часу t і t+ t, тобто він є вектором відносного переміщення.
83
Тому
lim |
µ/ ν |
= V |
|
(70) |
|
r |
|||
t→0 |
t |
|
|
|
|
|
|
Використовуючи (69) і (70), одержуємо
lim |
Vν −Vµ' |
= [ωe , Vr ]. (71) |
|
||
t→0 |
t |
|
Скориставшись визначенням похідної вектор функції, другий доданок у правій частині (68) записуємо в такий спосіб:
|
Vµ (t + |
t) −Vµ (t) |
. = |
dVµ |
= aµ = ae |
|
Мал.26 |
lim |
|
|
|
||
|
|
|
||||
|
t→0 |
t |
|
dt |
|
|
(72) (оскільки прискорення точки µ рухливого середовища є переносним прискоренням точки М).
Таким чином, з обліком (71) і (72) рівність (68) записується так
daVe = ае + [ωe , Vr ] , dt
що і було потрібно.
Неважко довести, що якщо переносний рух поступальне, то
daVe = ае .
dt
Як було відзначено в доказі попередньої леми, можна вважати, що цей результат міститься у формулі (66), якщо при поступальному переносному русі ωe = 0.
Лема 2 доведена. Уведемо визначення:
коріолісовим прискоренням точки, що рухається,
називається подвоєний векторний добуток кутової швидкості рухливого середовища на відносну швидкість точки:
аk = 2[ωe , Vr ]. |
(73) |
84
Теорема про додавання прискорень (теорема Коріоліса).
Абсолютне прискорення точки дорівнює геометричній сумі відносного, переносного і коріолісова прискорень:
|
аа |
= аr + ae + ak . |
(74) |
|||||||
Доказ. Запишемо теорему про додавання швидкостей (§2) |
|
|||||||||
|
Va = Vr + Ve |
(75) |
||||||||
і знайдемо абсолютну похідну лівої і правої частин рівності (75) |
|
|||||||||
|
daVa |
= |
daVr |
+ |
daVe |
. |
(76) |
|||
|
|
|
|
|
|
|||||
|
dt |
|
dt |
|
|
dt |
|
|||
Очевидно, |
|
|
|
|
|
|
|
|
||
|
|
|
daVa |
|
= aa . |
(77) |
||||
|
|
|
dt |
|||||||
|
|
|
|
|
|
|
|
|||
Потім, підставивши у формулу (61) замість и відносну швидкість Vr , будемо мати
|
|
|
daVr |
= |
drVr |
+[ωe ,Vr ] , |
(78) |
||
|
|
|
|
dt |
|
||||
|
|
|
|
|
|
dt |
|
||
але |
drVr |
= ar і (78) запишеться так: |
|
||||||
|
|
||||||||
|
dt |
|
|
|
|
|
|||
|
|
|
|
daVr |
|
= ar +[ωe ,Vr ] . |
(79) |
||
|
|
|
|
dt |
|
||||
|
|
|
|
|
|
|
|
|
|
Використовуючи (77), (79) і (66), запишемо (76) у наступному виді:
аа = аr + ae +2[ωe , Vr ] .
З огляду на, що 2[ωe , Vr ] = ak , одержуємо (74). Теорема доведена.
§ 4. Випадки рівності нулю коріолісова прискорення
Абсолютна величина коріолісова прискорення визначається за формулою
| ak | = 2 |ωe | |Vr| sin α , |
(80) |
85

де α – кут між напрямками ωe і Vr , але оскільки вектор ωe спрямований уздовж осі обертання рухливого середовища (інакше називаною віссю переносного обертання), то можна вважати, що α – кут між цією віссю і вектором Vr .
Дорівнюючи праву частину (80) нулю, дійдемо висновку, що
можливі наступні три випадки рівності нулю коріолісова прискорення:
1)ωe = 0 – випадок миттєвої зупинки обертання рухливого
середовища або випадок переносного поступального руху;
2)Vr = 0 – випадок миттєвої зупинки у відносному русі;
3)sin α = 0 (тобто α = 0 чи α = π) – випадок паралельності
відносної швидкості й осі переносного обертання.
§5. Правило Жуковського побудови коріолісова прискорення
Н.Е. Жуковським було запропоноване наступне зручне при рішенні задач на складний рух точки правило побудови вектора
коріолісова прискорення (мал.27) :
1) проводимо площину, перпендикулярну осі переносного обертання,
2)проектуємо відносну швидкість Vr на цю площину, 3)отриманий вектор Vr/ повертаємо на 90о у цій площині убік переносного обертання і множимо його на 2|ωе|.
Мал.27
§ 6. Приклад рішення задачі на складний рух точки
Рівнобедрений прямокутний трикутник АВС обертається зі стану спокою навколо катета АС з постійним кутовим прискоренням ε=1с-2. Уздовж сторони АВ рухається точка М за законом s=4t3 (м). Знайти
86
абсолютну швидкість і абсолютне прискорення точки М в момент часу t=2с, якщо ωο=0.
Рішення. У цій задачі переносним рухом є обертання трикутника відносно горизонтальної осі АС, а відносним – рух точки уздовж сторони АВ трикутника.
Відносна швидкість точки спрямована уздовж сторони АВ і дорівнює
Vr = ds = 12t2 dt
При t=2 с одержуємо Vr = 8 м/с. Відстань s=32м при t=2с.
Мал.28 Точка µ трикутника, з якою збігається точка М в цей момент часу, описує коло у площині, перпендикулярній осі обертання,
радіус якої h= ssin 450 = 16
 2 м. Швидкість точки µ є переносною швидкістю точки М и визначається по формулі для швидкості точки обертового тіла:
2 м. Швидкість точки µ є переносною швидкістю точки М и визначається по формулі для швидкості точки обертового тіла:
Ve = ωh .
Кутову швидкість обертання трикутника знаходимо з формули для равноприскореного обертання
ω = εt + ω0 = 2 c−1 ( ω0 = 0) .
Тоді Ve = 32
 2 м/с.
2 м/с.
Абсолютна швидкість точки М дорівнює геометричній сумі відносної і переносної швидкостей:
Va = Vr +Ve
і оскільки кут між Vr і Vе дорівнює 90о , те абсолютна величина Va визначається за формулою
Va = 
 Vr2 +Ve2 = 65,97м/с
Vr2 +Ve2 = 65,97м/с
Переходимо до визначення абсолютного прискорення. Оскільки відносний рух точки М прямолінійне, нормальне відносне
87

прискорення дорівнює нулю і повне відносне прискорення збігається з дотичним:
ar = ar,τ = dVr = 24t dt
При t=2с одержуємо ar=48м/с2. Спрямовано відносне прискорення уздовж сторони АВ.
Переносне прискорення точки М, тобто прискорення точки µ, складається з двох складових – дотичного і нормального прискорень, оскільки точка µ є точкою равноускоренно обертового тіла. Дотичне переносне прискорення дорівнює
ae,τ = εh = 16
 2 м/с2
2 м/с2
і спрямовано уздовж дотичної до кола, по якому рухається точка µ, а нормальне переносне прискорення дорівнює
ae,n = ω2h = 64
 2 м/с2
2 м/с2
іспрямовано уздовж радіуса цієї кола до її центра.
Для побудови коріолісова прискорення використовуємо правило Жуковського. Спочатку необхідно спроектувати вектор відносної швидкості на площину перпендикулярну осі обертання рухливого середовища, тобто на площину трикутника АВС. Такою площиною є площина кола, що описує точка µ. У результаті проектування Vr на
цю площину одержуємо вектор Vr/ , що спрямований уздовж радіуса кола протилежно напрямку ae,n . Величина Vr/ дорівнює
Vr/ = Vr cos450 = 24
 2 м/з2.
2 м/з2.
Далі вектор Vr/ необхідно повернути в згаданій вище площині на 90о
убік обертання трикутника. У такий спосіб одержуємо напрямок вектора коріолісова прискорення ак. Величина коріолісова прискорення визначається так:
ak = 2ωVr/ = 2 2 24
 2 = 96
2 = 96
 2 м/з2
2 м/з2
Абсолютне прискорення точки дорівнює геометричній сумі відносного, переносного і коріолісова прискорень, і оскільки переносне прискорення саме дорівнює сумі дотичної і нормальний складових, то приходимо до наступної формули:
aa=ar+ae,τ+ae,n+ak
Виберемо систему прямокутних координат у такий спосіб:
88

вісь y направимо паралельно осі обертання; тоді осі x і z будуть лежати в площині кола, описуваною точкою µ, причому вісь x горизонтальна, а z вертикальна.
Приведену вище рівність спроектуємо на осі координат. У результаті одержимо
aa,x = ae,τ + ak = 112
 2 м/з2
2 м/з2
aa,y = ar cos450 = 24
 2 м/з2
2 м/з2
aa,z = ar cos450 − ae,n = −40
 2 м/з2
2 м/з2
Тоді модуль абсолютного прискорення може бути знайдений з формули
aa = 
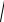 aa2,x + aa2, y + aa2,z = 171,58 м/з2
aa2,x + aa2, y + aa2,z = 171,58 м/з2
89
Г Л А В А IV
ПЛОСКОПАРАЛЕЛЬНИЙ РУХ ТІЛА
§ 1. Рівняння плоскопараллельного руху тіла
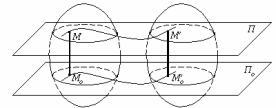
Рух тіла називається плоскопараллельным, якщо точки тіла
рухаються в площинах, паралельних деякий нерухомої площини По (мал.29).
Виберемо деяку точку М тіла. Вона рухається в площині П, паралельної площини По . Опустимо з цієї точки перпендикуляр на площину По. Нехай у підставі перпендикуляра зна- ходиться точка Мо цього тіла. Відрізок
Мал.29 ММо, перпендикулярний площини По в початковий момент, буде залишатися таким і надалі, оскільки інакше
принаймні одна з точок М чи Мо повинна була б вийти зі своєї площини. Звідси випливає, що всі точки тіла, що лежать на цьому перпендикулярі, рухаються по однакових траєкторіях і в кожен момент часу мають геометрично рівні швидкості і геометрично рівні прискорення. Тому замість того щоб вивчати плоскопаралельний
рух тіла можна вивчати рух точок, що лежать у підставі таких перпендикулярів, тобто рух плоскої фігури, що утвориться при
перетинанні тіла площиною По, у цій площині.
Проведемо в площині По нерухому систему координат хоОуо (мал.30). Виберемо деяку точку А плоскої фігури і проведемо через цю точку осі рухливої системи координат хАу, що при русі плоскої фігури повинні залишатися паралельними осям нерухомої системи хоОуо , тобто Ахо ||Ох, Ауо ||Оу. Розглянемо тепер аналогічно §1 глави III рух плоскої фігури як складний: рух плоскої фігури відносно нерухомої системи координат хоОуо будемо називати абсолютним, рух її відносно рухливої системи координат хАу – відносним, а рух рухливої системи координат хАу відносно нерухомої системи координат хоОуо –
переносним. Помітимо, що переносний рух є поступальним, оскільки
90
