
Курс теоретичної механіки 2007 (Укр)
.pdf
ни, паралельна силам, спрямована убік більшої з них і за модулем дорівнює абсолютній величині різниці величин сил. Точка прикладення рівнодіючої на продовженні відрізка, що з'єднує точки прикладення сил, поділяє цей відрізок у відношенні, зворотному величинам цих сил зовнішнім образом.
2.Пара сил.
Будемо розглядати пару сил як граничний випадок попередньої системи сил, при якому модуль сили F2 прагне до модуля сили F1, тобто в пропорції (16) необхідно зробити граничний перехід F2 → F1. Представимо її в наступному виді:
AB + BC = F2
BC F1
і визначимо з неї довжину відрізка ВР:
BC = AB F1 F2 − F1
Якщо F2 → F1, то F = F2 – F1 → 0, а ВР→ ∞, тобто точка прикладення рівнодіючої іде в нескінченність, а величина її прагне до
нуля. Це означає, що
пара сил рівнодіючої не має.
§ 18. Відмінності рівнодіючої від головного вектора
Геометрична рівність рівнодіючої і головного вектора не означає, що ці поняття тотожні. Треба їх розрізняти:
1.Головний вектор існує в будь-якої системи сил, а рівнодіюча не в кожної, як показує приклад 3 попереднього параграфа.
2.Головний вектор – це вільний вектор, а рівнодіюча – ковзний, тобто який можна переміщати уздовж лінії дії. Дійсно, це
можна виконати за допомогою елементарних операцій.
3.Головний вектор – це поняття геометричне, а
рівнодіюча – фізичне.
Головний вектор визначається геометричною операцією додавання сил, а рівнодіюча знаходиться за допомогою елементарних операцій, що мають визначений фізичний зміст (див. наступний параграф).
§19. Аксіоми статики
Ваксіомах статики формулюються найпростіші умови рівноваги тіл, закони взаємодії тіл при рівновазі, а також приводяться найпрос-
21
тіші дії, що не порушують рівноваги тіла. Аксіоми статики є результатом узагальнення величезної кількості спостережень у процесі практичної діяльності. Крім того, результати теорії, побудованої на базі цих аксіом, також піддалися багаторічній досвідченій перевірці.
Слід зазначити, що аксіоми статики є наслідком більш загальних аксіом, формулюмих у динаміці.
Аксіома 1. Для того щоб тіло під дією двох сил знаходилося в рівновазі, необхідно і досить, щоб ці сили були прямопротилежними.
Мал.20
Аксіома 2 (фізична властивість елементарних операцій).
Елементарні операції не порушують рівноваги тіла.
Наслідок 1. Тіло не може знаходитися в рівновазі під дією однієї
сили.
Доказ (від протилежного). Нехай тіло знаходиться під дією однієї сили F, прикладеної в точці А. Припустимо, що воно знаходиться в рівновазі. Використовуємо першу елементарну операцію: додамо дві
прямопротилежні сили Р1 і Р2, причому Р1 теж прикладена в точці А і має той же напрямок, що і F. Використовуємо тепер третю елементарну операцію і замінимо дві сили F і Р1 однією силою Q = F + P1. У результаті виявляється, що тіло знаходиться під дією двох сил
Мал.21 Q і Р2, причому Q = F+P1 > Р2 (тому що Р2 = Р1), тобто тіло знаходиться в
рівновазі під дією двох сил, що не є прямопротилежними, що суперечить першій аксіомі статики. Таким чином, наше припущення про те, що тіло знаходиться в рівновазі невірно.
Наслідок 2. Перенос сили уздовж її лінії дії з однієї точки
твердого тіла в іншу не порушує рівноваги тіла.
Такий перенос може бути здійснений за допомогою елементарних операцій (§13).
22

Аксіома 3 (рівність дії і протидії). Два тіла взаємодіють за допомогою прямопротилежних сил (мал.22).
Аксіома 4 (принцип твердіння). Рівновага деформуємого тіла
не порушиться, якщо воно стане абсолютно твердим.
Ця аксіома дозволяє використовувати умови рівноваги абсолютно твердого тіла при дослідженні рівноваги деформуємих тіл.
Тіла, на переміщення яких не накладені обмеження, називаються вільними. У протилежному випадку
Мал.22 тіла називаються невільними.
Тіла, що обмежують переміщення невільного тіла, називаються зв'язками.
Реакціями зв'язків називаються сили, з якими зв'язки діють на невільне тіло.
Аксіома 5 (принцип звільнення від зв'язків). Невільне тіло можна розглядати як вільне, якщо відкинути зв'язки і замінити їхні дії на тіло реакціями цих зв'язків.
§20. Основні типи зв'язків і їхні реакції.
1.Ідеально гладка поверхня.
Ідеально гладкої називається поверхня, що не чинить опору переміщенню тіла уздовж поверхні.
Реакція ідеально гладкої поверхні спрямована по нормалі до поверхні в точці зіткнення тіла і поверхні (тобто перпендикулярно до-
Мал.23 тичній площини до поверхні).
Це пояснюється тим, що в протилежному випадку реакція мала б складову в дотичній площині, що чинила б опір переміщенню тіла уздовж поверхні.
23

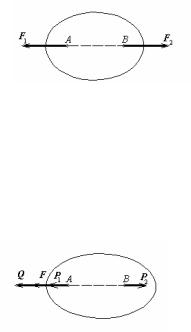
2. Зв'язок з нерухомою віссю обертання (нерухомий ци-
ліндричний шарнір, підшипник).
Невільне тіло прикріплене до вала підшипника (шарніра). Дотичні поверхні вала і підшипника передбачаються циліндричними і ідеально гладкими (мал.24а).
Мал.24
Тому реакція нерухомого циліндричного шарніра |
проходить |
через вісь шарніра, лежить у площині, перпендикулярній осі, і розкладається на дві складові в цій площини (мал.24б).
3. Зв'язок з нерухомим центром обертання (нерухомий сферичний шарнір, підп'ятник).
|
Сферичний |
шарнір |
||
|
являє собою кулю, що |
|||
|
знаходиться в сферич- |
|||
|
ній |
порожнині |
(мал. |
|
|
25а). |
Такий |
зв'язок |
|
|
залишає |
нерухомим |
||
|
цетр кулі, зв'язаного з |
|||
|
невільним тілом. |
|||
|
Дотичні поверхні |
|||
|
вважаються идеаль – |
|||
Мал.25 |
но гладкими, тому ре- |
|||
|
акція |
спрямована уз- |
||
довж нормалі до сфери, тобто |
уздовж її радіуса, а тим самим через |
|||
центр. Крім того, тому що положення точки дотику поверхонь заздалегідь невідомо, то невідомий і напрямок реакції. Таким чином,
реакція сферичного шарніра проходить через його центр, може мати довільний напрямок у просторі і тому розкладається на три складові уздовж трьох осей координат (мал.2бб).
24
Три складових має також реакція підп'ятника (упорного підшипника), що перешкоджає зсуву кінця вала в будь-якому напрямку (мал.26).
Мал.26
4.Ідеально гнучка невагома нерозтяжна нитка.
Реакція нитки спрямована уздовж нитки й усередину її, тому що відхилення реакції від напрямку нитки означало б, що нитка чинить опір вигину, що суперечить її ідеальної гнучкості(мал.27).
Мал.27
5.Абсолютно твердий невагомий прямолінійний стержень із шарнірами на кінцях.
Реакція стержня спрямована уздовж його осі,
тому що відхилення напрямку реакції від осі стержня означало б наявність сил опору в шарнірах, але у ньому дотичні поверхні ідеально гладкі. При цьому реакція може бути спрямована як усередину стержня, так і назовні, у залежності від того, розтягнутий він чи стиснутий (мал.28).
Мал.28
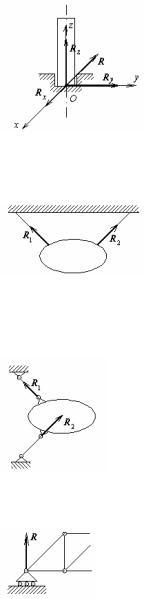
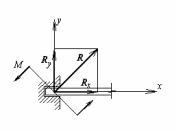
6.Шарнірно-рухлива опора.
Являє собою комбінацію з двох типів зв'язків: нерухомого циліндричного шарніра і ідеально гладкої поверхні, уздовж якої може переміщатися шарнір. Тому
реакція шарнірно-рухливої опори проходить через
вісь шарніра і спрямована перпендикулярно повер- Мал.29 хні, уздовж якої опора може пере міщатися
25
(мал.29).
7.Жорстке закладення.
Тому що жорстке закладення перешкоджає переміщенню кінця невільної балки як по горизонталі, так і по вертикалі, то реакція
твердого закладення має дві складові: горизонтальну і вертикальну. Крім того, у жорсткому закладенні присутня і
реактивна пара сил з невідомим моментом М, тому що жорстке закладення перешкоджає повороту кінця балки.
Мал.30
26
Г Л А В А II
УМОВИ РІВНОВАГИ ТІЛА
§ 1. Основна лема статики
Будь-яку систему сил за допомогою елементарних операцій
можна привести до двох сил.
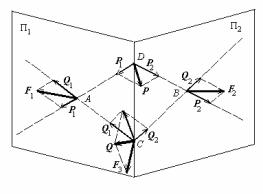
Доказ. Доведемо спочатку лему для того випадку, коли вихідна
|
система сил |
склада- |
|
|
ється з трьох сил F1, |
||
|
F2, F3, прикладених у |
||
|
точках А, В и С (мал. |
||
|
31). |
Будемо |
вважати |
|
при |
цьому, |
що ніякі |
|
дві сили з цих трьох |
||
|
(зокрема, F1 і F2) не |
||
|
лежать в одній пло- |
||
|
щині, оскільки інакше |
||
|
доказ був тривіальний. |
||
|
Проведемо |
площину |
|
|
Π1 через лінію дії сили |
||
|
F1 і точку С. |
|
|
Мал.31 |
Потім проведемо пло- |
||
|
щину Π2 через лінію дії |
||
сили F2 і точку С. Ці площини перетинаються, тому що вони мають |
|||
загальну точку С. Виберемо |
довільну точку D (відмінну від точки |
||
С) на лінії перетинання площин і проведемо дві прямі в площині Π1: одну – через точки А и С, іншу – через точки А и D. Ці дві прямі задають два напрямки, що проходять через точку А, уздовж яких ми розкладемо силу F1 на дві складові Р1 і Q1. Це можна здійснити за допомогою елементарних операцій (див. §13 глави I). Потім аналогічно проведемо в площині Π2 дві прямі: одну – через точки В и С, іншу – через точки В и D. Вони задають два напрямки, що проходять через точку В, уздовж який розкладемо силу F2 на дві складові Р2 і Q2. Перенесемо, використовуючи елементарні операції, сили Р1 і Р2 уздовж їхніх ліній дії в точку D. Потім застосуємо третю елементарну операцію: замінимо сили Р1 і Р2, прикладені в точці D, однією силою Р, прикладеної в цій точці. Аналогічно, перенесемо,
27
сили Q1 і Q2 уздовж їхніх ліній дії в точку С и, двічі застосувавши третю елементарну операцію, замінимо сили F3, Q1 і Q2, прикладені в точці D, однією силою Q, прикладеної в цій точці. У результаті залишаються тільки дві сили: Р, прикладена в цій точці D, і Q, прикладена в точці С.
Якщо вихідна система складається з більшого, ніж три, числа сил, то, вибравши будь-які три з них, приводимо їх, використовуючи доведений окремий випадок леми, за допомогою елементарних операцій до двох сил. Таким чином, число сил у системі зменшується на одиницю. Так продовжуємо доти, поки число сил не стане рівним двом.
Лема доведена.
§ 2. Основна теорема статики (геометричні умови рівноваги довільної системи сил)
Для того щоб тіло під дією довільної системи сил S{F1,F2,…,Fn}знаходилося в рівновазі, необхідно і досить, щоб
головний вектор і головний момент відносно довільно обраного
полюса цієї системи сил дорівнювали нулю.
Доведемо необхідність умов рівноваги (тобто покажемо, що з рівноваги тіла випливає рівність нулю головного вектора і головного моменту системи сил, що діють на тіло).
Розіб'ємо доказ на ряд етапів:
1.Використовуємо основну лему і приводимо за допомогою еле-
ментарних операцій систему S{F1,F2,…,Fn} до системи S1{P,Q}, що складається з двох сил. Як випливає з аксіоми 2, рівновага тіла при цьому не порушиться.
2.Тіло виявляється в рівновазі під дією двох сил P і Q. З аксіоми 1 випливає, ці сили є прямопротилежними.
Тоді
R (S1) =P + Q = 0,
M0 (S1) = m0(P) + m0(Q) = 0
(О – довільний полюс), причому друга рівність випливає з властивості 3 моменти сили відносно полюса (§4 глави I).
3. Оскільки системи S1{P,Q} і S{F1,F2,…,Fn}еквівалентні, то
R (S) = R (S1) = 0, M0 (S) = M0 (S1) = 0,
28
(що і було потрібно довести).
Доведемо достатність умов рівноваги (тобто покажемо, що з рівності нулю головного вектора R системи сил, що діють на тіло, і головного моменту її M0 відносно довільно обраного полюса О
випливає, що тіло знаходиться в рівновазі).
Розіб'ємо доказ на ряд етапів:
1. Використовуємо основну лему і приводимо за допомогою елементарних операцій систему S{F1,F2,…,Fn}до системи S1{P,Q}, що складається з двох сил. Як випливає з геометричних властивостей елементарних операцій, головний вектор і головний момент системи сил залишаться при цьому незмінними, тобто
R (S1) = R (S) = 0,
M0 (S1) = M0 (S) = 0.
2.Звідси випливає, що
P + Q =R (S1) = 0,
m0(P) + m0(Q) =M0 (S1) = 0.
Такими властивостями володіють тільки дві прямопротилежні сили, тобто
S1{P,Q} – п.п.с.
3. Таким чином, тіло виявилося під дією двох прямопротилежних сил. Відповідно до аксіоми 1 воно знаходиться в рівновазі. Якщо здійснити зворотний перехід від системи S1{P,Q} до системи S{F1,F2,…,Fn}за допомогою елементарних операцій, то рівновага тіла не порушиться, тобто воно буде знаходитися в рівновазі під дією системи сил S{F1,F2,…,Fn}...
Теорема доведена.
§ 3. Аналітичні умови рівноваги довільної системи сил
Для того щоб тіло під дією довільної системи сил знаходилося в рівновазі, необхідно і досить, щоб виконувалися рівняння рівноваги:
29
n |
n |
n |
|
|
1) ∑прx Fk = 0, 2) |
∑прy Fk |
= 0, 3), ∑прz Fk = 0, |
|
|
k=1 |
k=1 |
k=1 |
(17) |
|
n |
n |
n |
||
|
||||
4) ∑mx Fk = 0, 5) |
∑my Fk = 0, 6) ∑mz Fk = 0. |
|
||
k=1 |
k=1 |
k=1 |
|
|
Доказ.
Знайдемо проекції головного вектора і головного моменту на осі координат
n |
n |
|
Rx = прx R = прx ∑Fk = ∑прx Fk , |
|
|
k=1 |
k=1 |
|
n |
|
|
Ry = ∑прy Fk , |
|
|
k=1 |
|
|
n |
|
|
Rz = ∑прz Fk , |
|
|
k=1 |
|
(18) |
|
|
|
n |
n |
n |
M ox = прx Mo = прx ∑mo (Fk ) = ∑прx mo (Fk ) = ∑mx (Fk ), |
||
k=1 |
k=1 |
k=1 |
n
M oy = ∑my (Fk ), k=1
n
M oz = ∑mz (Fk ). k=1
При висновку останніх трьох рівностей ми скористалися теоремою про проекцію суми векторів на вісь (див. Додаток 1), а також залежністю між моментами сили відносно полюса й осі.
Рівність нулю головного вектора і головного моменту еквівалентно рівності нулю їхніх проекцій на всі осі координат. Тоді з основної теореми статики випливає, що для того щоб тіло знаходилося в рівновазі, необхідно і досить, щоб виконувалися наступні рівності:
Rx = 0, Ry = 0, Rz = 0, Mox = 0, Moy = 0, Moz = 0. |
(19) |
Підставивши сюди вираження для проекцій головного вектора і головного моменту з (18), одержуємо необхідне. Теорема доведена.
30
