Курс теоретичної механіки 2007 (Укр)

Позначимо величину цих рівних кутів через α. Якщо тепер повернути тіло з положення I навколо осі Оp’ ( щопроходить через точку С) на кут α (напрямок обертання показаний на кресленні), то точка А1 перейде в точку А2, а точка В1 – у точку В2, причому точка О залишиться на місці. Це значить, що при цьому тіло з положення I перейде в положення II, що і було потрібно. Теорема доведена.

Уведемо для обертання тіла з положення I у положення II вектор середньої кутової швидкості ωср за проміжок часу t у такий спосіб: направимо його уздовж осі обертання у відповідну сторону (див. §5 глави II), а величину визначимо так:

§ 3. Вісь миттєвого обертання. Миттєва кутова швидкість. Перша формула Эйлера

Нехай тепер t → 0. При цьому вісь кінцевого обертання Оp’ буде повертатися навколо точки О. Граничне положення Ор осі кінцевого

обертання Op' при прагненні до нуля проміжку часу називається

віссю миттєвого обертання.

Середня кутова швидкість ωср, будучи спрямованої уздовж осі кінцевого обертання, у границі буде спрямована уздовж осі миттєвого

101

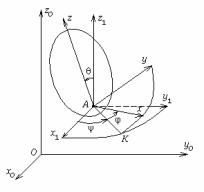
Таким чином, можна представляти, що в кожен момент часу тіло, що має нерухому точку, робить миттєве обертання навколо осі миттєвого обертання ОР з кутовою швидкістю, рівної миттєвої кутової швидкості ω. Тому можливо використання першої формули Эйлера (§5 глави II) і для визначення швидкостей точок тіла, що має одну нерухому точку:

§ 4. Рух вільного твердого тіла (довільний рух тіла). Рівняння руху

Нехай на рух твердого тіла відносно нерухомої системи координат Оxоyоzо не накладено ніяких обмежень. Виберемо деяку точку А тіла і проведемо через неї осі рухливої системи координат Ах1y1z1 паралельно осям нерухомої системи координат (мал.43). У подальшому русі вони повинні залишатися паралельними нерухомим осям.

Розглянемо тепер рух вільного тіла як складне.

Переносний рух, тобто рух

тіла розкладено на поступальне й обертання навколо нерухомої точки.

Точка А тіла, що є початком рухливої системи координат, називається полюсом розкладання вільного руху на поступальне й

обертальне.

Очевидно, рівняннями руху вільного тіла будуть рівняння переносного і відносного рухів.

Оскільки поступальний рух рухливої системи визначається рухом

102

початку координат, то рівняннями переносного руху є рівняння руху точки А.

Для запису рівнянь відносного обертання необхідно ввести ще одну систему координат Аxyz, жорстко зв'язану з тілом. Її положення відносно системи Ах1y1z1 визначається кутами Эйлера, завдання яких як функцій часу дає рівняння відносного руху.

Таким чином, рівняння вільного руху тіла мають наступний вид: x0A = f1 (t), y0A = f2 (t), z0A = f3 (t), θ = f4 (t), ψ = f5 (t), φ = f6 (t). (96)

Кутова швидкість відносного обертання не залежить від вибору полюса

розкладання.

Дійсно, візьмемо два різних полюси розкладання А1 і А2 і відповідно дві рухливі системи ко-

ординат А1x1y1z1 і А2x2y2z2 , паралельні осям нерухомої системи.

Крім того, проведемо через кожний з полюсів осі систем координат А1xyz і А2x/y/z/, жорстко зв'язані з тілом, паралельно один одному (мал.44).

Мал.44 У результаті кути Эйлера в полюсах виявляться рівними:

θ1 = θ2 , ψ1 = ψ2 , φ1 = φ2.

Це значить, що обертання тіла відносно полюсів А1 і А2 ідентично, а отже, у кожен момент часу миттєві кутові швидкості обертання ω1 і ω2 геометрично рівні.

§ 5. Друга формула Эйлера

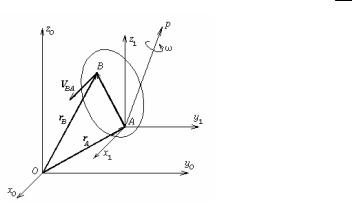
Нехай А – полюс розкладання вільного руху тіла на поступальне й обертальне, а В − довільна точка тіла (мал.45). Проведемо радіусвектори точок А и В з початку нерухомої системи координат, а також

103

Диференціюючи рівність (97) за часом, одержуємо

танні тіла навколо точки А.. Таким чином, (98) записується

тобто швидкість будь-якої

точки вільного твердого тіла

дорівнює швидкості довільно

Мал.45

обраного полюса, геометрич-

но складеної зі швидкістю

цієї точки у відносному обертанні тіла відносно полюса.

Використовуючи формулу (95) параграфа 3 (тобто першу формулу Эйлера), VBA може бути записане так:

а тоді (99) представиться в наступному виді:

Формула (101) (чи спільно формули (99) і (100)) і зветься другою формулою Эйлера.

Наслідки.

1)Проекції швидкостей точок тіла на напрямок вектора

ωрівні.

Дійсно, вектор VBA перпендикулярний вектору ω як одному зі співмножників векторного добутку (100), і тому його проекція на напрямок вектора ω дорівнює нулю. Проектуючи (99) на цей напрямок, одержуємо

прω VB =прω VB .

104

Зовсім аналогічно доводиться наслідок

2)Проекції швидкостей двох точок тіла на вісь, що проходить через ці точки рівні.

105

Другий закон. Сила, що діє на матеріальну точку, надає їй прискорення, що у інерціальній системі відліку пропорційно

величині сили і має напрямок, що збігається з напрямком сили.

Математично цей закон виражається у виді рівності

де m – маса точки, а – її прискорення, F – сила, що діє на точку.

Третій закон (закон незалежності дії сил). Якщо на матеріальну точку діє кілька сил, то її прискорення в інерціальній системі

відліку дорівнює геометричній сумі прискорень, викликуваних кожної із сил окремо, тобто

k=1

де аk - прискорення, викликане силою Fk (k=1,2,…,n)...

За попереднім законом ak = Fk / m . Підставляючи це в (2), одержуємо

k=1

Звичайно третій закон записують у виді рівності (3). Це рівність ще зветься «основне рівняння динаміки матеріальної точки».

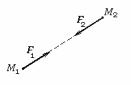
Четвертий закон (закон рівності дії і протидії). Будь-яка взаємодія двох матеріальних точкок здійснюється за допомогою

двох прямопротилежних сил.

Нагадуємо, що дві сили називаються прямопротилежними, якщо вони лежать на одній прямій, спрямовані в протилежні сторони і рівні по величині (мал.1).

Мал.1

П'ятий закон (закон всесвітнього тяжіння). Будь-які дві матері альні точки притягаються друг до друга силами, прямо пропорційними добутку їхніх мас і обернено пропорційни ми квадрату відстані між ними:

107

Тут m1 і m2 – маси точок, r – відстань між ними, γ – гравітаційна постійна.

§2. Основні задачі динаміки матеріальної точки. Рішення першої задачі

До основних задач динаміки матеріальної точки відносяться

1)перша задача: заданий рух точки, необхідно знайти силу, що діє на точку;

2)друга задача: задані сили, що діють на точку, необхідно

знайти закон руху точки.

Як приклад рішення першої задачі динаміки точки розглянемо проблему визначення залежності між вагою матеріальної точки і її масою.

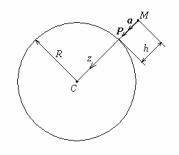
Нехай деяка матеріальна точка маси m вільно падає без початкової швидкості з деякої висоти h на поверхню Землі (мал.2). Можна показати, що сила Р гравітаційного притягання до Землі спрямована до центра Землі, а величина її може бути обчислена за формулою (4) у припущенні, що маса Землі зосереджена в її цетрі:

Будемо вважати, що висота h, з якої падає точка, набагато менше радіуса Землі, і тому R + h з великим ступенем точності дорівнює R . Тоді

і підставимо замість Р вираження (5). У результаті будемо мати

108

З (7) випливає, що прискорення вільного падіння тіла не залежить від маси цього тіла − факт, експериментально відкритий ще Галилеем. Надалі будемо позначати його буквою g. Тоді (6) запишеться так:

Ця формула виражає залежність між масою і вагою тіла.

§3. Диференціальні рівняння руху матеріальної точки. Рішення другої задачі динаміки

У класичній механіці сили, що діють на матеріальну точку, вважаються залежними від положення точки, її швидкості і часу, тобто в загальному випадку

(r – радіус-вектор точки).

Тоді основне рівняння динаміки (3) запишеться так:

Спроектувавши (10) на осі декартовой системи координат, одержимо диференціальні рівняння руху точки:

109

Якщо сили, що діють на точку, відомі, то вираження в правих частинах (11) являють собою задані функції своїх аргументів, і знаходження рівнянь руху

x = f1 (t), y = f2 (t), z = f3 (t)

зводиться до інтегрування диференціальних рівнянь (11).

Тому послідовність рішення другої задачі динаміки матеріальної

точки складається з наступних операцій:

1) складання диференціальних рівнянь руху точки;

2)інтегрування диференціальних рівнянь;

3)визначення постійних інтегрування з заданих початкових умов;

4)знаходження шуканих величин і дослідження отриманих результатів.

§4. Приклади рішення другої задачі динаміки

1. Прямолінійний рух точки під дією сили, залежної від часу. Задача. Тіло масою m = 2 кг починає рухатися зі стану спокою уздовж горизонтальної шероховатої площини, коефіцієнт тертя якої

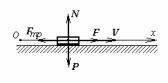
дорівнює f = 0.1, під дією сили F = 4t2 (Н). Знайти закон руху тіла. Рішення. Виберемо початок відліку

в початковому положенні тіла і направимо вісь х убік руху. Тоді початкові умови руху тіла запишуться так:

що діють на тіло. Це вага Р, задана сила F, нормальна реакція поверхні N і сила тертя Fтр. Складаємо основне рівняння динаміки

ma = F+P+N+Fтр

і проектуємо його на вісь х

110