
Курс теоретичної механіки 2007 (Укр)
.pdf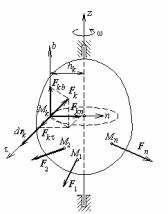
|
dsk = hk ω dt = hk dφ. |
|
|
Підставляючи в (128), одержуємо |
|
|
dA ( Fk ) = Fkτ hk dφ. |
(129) |
|
Знайдемо момент сили Fk |
відносно |
|
осі z: |
|
|
mz (Fk ) = mz (Fkτ )+mz (Fkn )+mz (Fkb ) = |
|
|
= Fkτ hk . |
|
|
Зіставивши це з (129), дійдемо |
|
|
висновку, що |
|
|
dA ( Fk ) = mz (Fk ) dφ. |
(130) |
Мал.36 |
Сумарна елементарна робота всіх сил, |
|
|
прикладених до обертового тілу, дорів- |
|
нює |
|
|
|
n |
|
|
dA = ∑dA(Fk ) = M z dφ, |
(131) |
k=1
n
де M z = ∑mz (Fk ) .
k=1
Робота сил, прикладених до обертового тілу на кінцевому його переміщенні, дорівнює
φ1 φ1
A = ∫dA = ∫M z dφ,
φ0 φ0
де φ0 − кутова координата початкового положення тіла, а φ1 − кінцевого. Якщо припустити, що Mz не залежить від положення тіла, тобто від кутової координати φ, те формула прийме наступний вид
φ1 |
|
A = M z ∫dφ = M z (φ1 − φ0 ) . |
(132) |
φ0 |
|
Таким чином, робота сил, прикладених до обертового твердого
тіла, дорівнює добутку суми моментів сил відносно осі обертання на кут повороту тіла (за умови, що сума моментів сил відносно осі
151

обертання незмінна).
5. Елементарна робота сил, прикладених до плоскої фігури.
Нехай плоска фігура рухається у своїй площині під дією системи сил F1 , F2 ,…,Fn(мал. 37). Швидкості точок, а значить і їхні елементарні переміщення розподіляються на плоскій фігурі так, начебто вона виконує обертання навколо осі z, перпендикулярної площини фігури і минаючої через миттєвий центр обертання Р. Тому елементарна робота сил, прикладених до плоскої фігури відповідно до формули (131) дорівнює
dA = M zp dφ ,
де M zp − сума моментів сил відносно осі z .
Запишемо формулу зміни головного моменту системи сил відносно полюса при зміні полюса (§11 глави I частини I)
MP = MА +[R , PA ]
(А − довільно обрана точка плоскої фігури). Спроектуємо ліву частину рівності на вісь z , а праву на паралельну їй вісь z, що проходить
Мал.37 через точку А. У відповідності з формулою (12) §11 глави I частини I будемо мати
M zP = M z + R| PA |sin α
( M zP і Mz − суми моментів сил відносно осей z і z відповідно, крім
того, враховано, що вектор [R , PA ] паралельний осі z ). Множачи отриману рівність на dφ, будемо мати
d = M z dφ + R | PA | dφ sin α .
Але | PA | dφ = d A , де dА − переміщення точки А, а sin α =cos (90o −
α)= =cos β ( β − кут між векторами R і PA ). Таким чином, попередня рівність може бути записане так
dA = Mz dφ + R dΑ cos β = Mz dφ + (R , dΑ ). |
(133) |
152

§14. Теорема про зміну кінетичної енергії точки
Кінетичною енергією точки називається скалярна величина, рівна половині добутку маси точки на квадрат її швидкості:
T = mV2 2 .
Теорема. Збільшення кінетичної енергії точки на кінцевому її переміщенні дорівнює сумі робіт сил, прикладених до точки, на цьому переміщенні, тобто
mV 12 |
− |
mV02 |
= |
n |
A(F ) . |
(134) |
2 |
|
∑ |
||||
2 |
|
k |
|
|||
|
|
|
|
|
|
|
|
|
|
|
k=1 |
|
|
Доказ. Нехай |
точка М рухається з положення М0 у положення М1 |
|||||||||||
|
під дією сил F1 , F2 , …, Fп (мал.38). |
|||||||||||
|
Складемо основне рівняння динаміки |
|||||||||||
|
|
|
|
|
|
n |
|
|
|
|||
|
|
|
ma = ∑Fk |
|
|
|
||||||
|
|
|
|
|
k=1 |
|
|
|
||||
|
і спроектуємо його на напрямок дотичної |
|||||||||||
|
|
|
|
|
|
n |
|
|
|
|||
|
|
|
maτ = ∑Fkτ . |
(135) |
||||||||
|
|
|
|
|
|
k=1 |
|
|
|
|||
|
Представимо дотичне прискорення аτ у слі- |
|||||||||||
|
дуючому вигляді: |
|
|
|
|
|
|
|
||||
Мал.38 |
a |
|
= |
dV |
= |
dV |
|
ds |
= |
dV |
V |
|
τ |
dt |
ds dt |
ds |
|||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
і підставимо це в (135), помноживши обидві частини рівності на ds:
n |
|
mVdV = ∑Fkτds . |
(136) |
k=1
Легко переконатися в тім, що ліва частина рівності (136) являє собою диференціал кінетичної енергії:
d( |
mV |
2 |
) = |
d |
( |
mV 2 |
)dV = mVdV , |
|
|
|
|
||||
2 |
|
|
dV |
2 |
|
||
а права − суму елементарних робіт сил:
n |
n |
∑dA(Fk ) = ∑Fkτds |
|
k=1 |
k=1 |
(див. формулу (121)).
153

Тоді (136) буде виглядати так |
|
|
|
||
d( |
mV 2 |
) = |
n |
dA(F ) . |
(137) |
|
∑ |
||||
2 |
|
k |
|
||
|
|
|
|
|
|
k=1
Проінтегруємо обидві частини рівності (137) уздовж переміщення
М0М1 точки М |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d( |
mV |
2 |
) = |
n |
|
|
dA(F ) . |
|||
∫ |
|
|
∑ |
∫ |
||||||||
|
|
2 |
|
|
|
|
k |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
M0M1 |
|
|
|
k=1 M0M1 |
|
|
||||||
З огляду на те, що швидкість |
|
точки М в початковому положенні |
||||||||||
дорівнює V0 , а в кінцевому − V1 , одержуємо |
|
|||||||||||
|
mV 2 |
|
mV 2 |
|
|
n |
|
|
|
|||
|
|
2 |
|
|
2 |
|
∑ |
|
|
|
||
|
|
0 |
− |
1 |
= |
|
|
A(F |
|
) , |
||
|
|
|
|
|
|
|
|
k |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
що і було потрібно. |
|
|
|
|
|
|
|
|
|
|
|
|
§15. Теорема про зміну кінетичної енергії механічної системи |
||||||||||||
Кінетичною енергією |
|
механічної |
системи називається |
|||||||||
скалярна величина, рівна сумі кінетичних енергій точок системи
n |
2 |
T = ∑ |
mkVk |
. |
|
2 |
|||
k=1 |
|
||
|
|
Теорема. Збільшення кінетичної енергії механічної системи на кінцевому її переміщенні дорівнює сумі робіт зовнішніх і внутрішніх сил, прикладених до точок системи, на цьому переміщенні:
n |
n |
|
T1 −T0 = ∑A(Fke ) + ∑A(Fki ) . |
(138) |
|
k=1 |
k=1 |
|
Доказ. Запишемо теорему про зміну кінетичної енергії для кожної точки механічної системи
|
mkVk21 |
− |
mkVk20 |
= A(F e ) + A(F i ) (k = 1,2,…,n)(139) |
|||
|
|
|
|||||
2 |
|
|
2 |
|
k |
k |
|
|
|
|
|
|
|||
Тут Vk0 − швидкість |
|
точки Мk |
у початковому її положенні, Vk1 − її |
||||
швидкість у кінцевому положенні, Fke − геометрична сума зовнішніх
154
сил, прикладених до |
|
точки Мk , |
Fki − геометрична сума внутрішніх |
|||||||
сил. |
|
|
|
|
|
|
|
|
|
|
Cумуючи рівності (139) по всіх |
точках системи, одержимо |
|||||||||
n |
mkVk21 |
− |
n |
mkVk20 |
= |
n |
A(F e ) + |
n |
A(F i ) , |
|
∑ |
2 |
∑ |
2 |
∑ |
∑ |
|||||
|
|
k |
k |
|||||||
|
|
|
|
|
|
|
|
|||
k=1 |
|
|
k=1 |
|
|
k=1 |
|
k=1 |
|
|
що збігається з (138). |
|
|
|
|
|
|
|
|
||
§16. Кінетична енергія твердого тіла в різних випадках руху
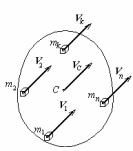
1. Поступальний рух. Уявно розіб'ємо тіло, виконуюче поступальний рух, на елементарні маси (частина з них показана на мал.39). Оскільки при поступальному русі швидкості точок тіла геометрично рівні (§1
глави II частини II), то
V1 = V2 =…=Vn=VС
(VC − швидкість центра мас тіла). Тоді
|
n |
2 |
n |
2 |
|
2 |
|
|
T = ∑ |
mkVk |
= ∑ |
mkVC |
= |
MVC |
. (140) |
|
2 |
2 |
2 |
||||
|
k=1 |
k=1 |
|
|
|||
|
|
|
|
|
|
||
Мал.39 |
Таким чином, |
|
|
|
|
||
кінетична енергія поступально рухається твердого тіла дорівнює половині добутку маси тіла на квадрат швидкості його центра мас.
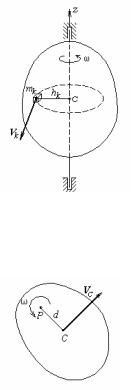
2. Обертання тіла навколо нерухомої осі. І в цьому випадку розбиваємо тіло на елементарні маси (одна з них показана на мал.40). Швидкість елементарної маси mk визначається за формулою
Vk = ω hk
( hk − відстань від елементарної маси до осі обертання). Тоді
|
n |
mkVk2 |
|
ω2 |
n |
|
|
2 |
|
T = |
∑ |
|
= |
|
∑ |
m |
h |
k |
. (141) |
2 |
2 |
||||||||
|
|
|
|
|
|
k |
|
|
|
|
k=1 |
|
|
|
k=1 |
|
|
|
|
155
Сума, що стoїть в правій частині формули (141) уже раніше зустрічалася (§8 глави II частини III). Це момент інерції Jz тіла відносно осі обертання z. Отже, (141)
можна записати так
T = |
J |
z |
ω2 |
, |
(142) |
|
|
2 |
|||
|
|
|
|
|
тобто кінетична енергія тіла, що
обертається навколо нерухомої осі, дорівнює половині добутку моменту інерції тіла відносно осі обертання на квадрат його кутової швидкості.
Мал.40
3.Плоскопаралельний рух тіла. Як показано в §5 глави IV
частини II, швидкості точок тіла при такому русі розподіляються так, ніби тіло робило обертання навколо осі, що проходить через миттєвий центр швидкостей перпендикулярно площини руху (мал.41). Тоді відповідно до формули (142)
кінетична енергія тіла визначається за формулою
|
|
|
|
|
|
|
|
|
T = |
J |
z |
ω2 |
|
(143) |
|||
|
|
|
|
|
|
|
|
|
|
|
P |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
За теоремою Гюйгенса−Штейнера (див. §10) |
|||||||||||||||||
Мал.41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
z |
|
= J |
z |
|
|
+ Md 2 |
|
|||
|
|
|
|
|
|
|
|
P |
|
|
C |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(тут d = CР). Підставивши це в (143), будемо мати |
|
|
|||||||||||||||
T = |
J zC ω2 |
|
+ |
|
M (ωd)2 |
. |
|
|
|||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Але ωd = Vc , і одержуємо остаточно |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
MV |
2 |
|
|
|
J z |
ω2 |
|
|
|
|
|
||||
T = |
|
c |
+ |
|
|
C |
|
|
|
|
. |
|
(144) |
||||
2 |
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким чином, кінетична енергія тіла, що виконує
плоскопаралельний рух, дорівнює кінетичної енергії поступального руху зі швидкістю центра мас, складеної з кінетичною енергією обертального руху навколо осі, що проходить через центр мас.
156

4. Довільний рух тіла. Якщо вибрати в якості полюса розкладання довільного руху тіла на поступальне й обертальне центр мас С, то згідно другій формулі Эйлера (§5 глави V частини II) швидкість будь-якої елементарної маси mk може бути представлена так
|
|
|
|
|
|
|
|
|
|
|
V |
k |
= V +V |
/ |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де |
Vk/ − |
швидкість |
|
маси |
mk у |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
відносному |
|
|
|
|
обертанні |
тіла |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
навколо |
|
точки С. При цьому за |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
модулем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
/ |
|
= ωh |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(hk − відстань від маси mk до осі |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
миттєвого обертання Ср. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V 2 |
= |
(V |
k |
,V |
k |
) |
= |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (V |
C |
+V |
/ |
,V |
C |
+V |
/ ) |
= |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= V |
2 |
+V |
/ 2 + 2 (V |
C |
,V |
/ ) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знайдемо кінетичну енергію |
|||||||||||||||||||
|
|
|
Мал.42 |
|
|
|
|
|
|
|
|
|
тіла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n |
mkVk2 |
|
1 |
|
n |
|
|
|
2 |
|
1 |
|
|
n |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
/ |
|
|
||
T = |
∑ |
|
= |
|
|
∑ |
m |
k |
V |
C |
+ |
|
|
∑ |
m |
k |
h |
k |
|
ω + (V |
C |
, |
|
∑ |
m |
k |
V |
k |
) . (145) |
||||||||||||
2 |
2 |
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
k=1 |
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Помітимо, що відповідно до формули (89) сума ∑mkVk/ |
, що стoїть в |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
правій частині (145), дорівнює |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑mkVk/ = MVC/ = 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
оскільки швидкість |
точки С в відносному обертанні тіла навколо цієї |
||||||||||||||||||||||||||||||||||||||||
ж точки дорівнює нулю. Тоді (145) запишеться так |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
MV |
2 |
|
|
|
JCp ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
T = |
|
|
C |
+ |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(146) |
||||
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
157
n |
n |
оскільки ∑mk |
= M , ∑mk hk2 = JCp (JCp − момент інерції тіла |
k=1 |
k=1 |
відносно осі миттєвого обертання Ср). Таким чином,
кінетична енергія твердого тіла у довільному русі дорівнює кінетичної енергії поступального руху зі швидкістю центра мас, складеної з кінетичною енергією обертального руху навколо осі миттєвого обертання, що проходить через центр мас.
§17. Приклад рішення задачі з використанням теореми про зміну кінетичної енергії
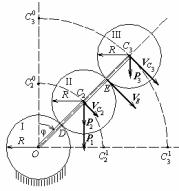
Задача. Епіціклічний механізм |
складається з трьох зубчастих |
||||
|
коліс однакового радіуса R = 1 м |
||||
|
(мал.43), одне з яких нерухомо, і |
||||
|
кривошипа, що обертається навколо |
||||
|
осі, що проходить через центр |
||||
|
нерухомого колеса. |
Колеса, |
що |
||
|
рухаються, |
прикріплені |
до |
||
|
кривошипа за допомогою осей, що |
||||
|
проходять через центри коліс. У |
||||
|
процесі руху механізму |
під дією сил |
|||
|
ваги |
з початкового вертикального |
|||
|
положення |
спокою |
кривошип |
||
|
здобуває |
кутову швидкість, |
що |
||
|
залежить від кута φ між вертикал- |
||||
|
лю і віссю кривошипа. |
|
|
||
Мал.43 |
Визначити кутову швидкість, що |
||||
|
придбає кривошип у той момент, ко- |
||||
ли кут φ стане рівним 90о. Маса кривошипа m1 = 5 кг, а маса коліс m2 = 2 кг. Колеса вважати однорідними дисками.
Рішення. Для рішення задачі використовуємо |
теорему про зміну |
кінетичної енергії механічної системи: |
|
T1 − T0 = Ae + Ai. |
(147) |
Будемо вважати, що зв'язки, що утворяють систему з окремих тіл, а також тіла з окремих часток, ідеальні (більш докладно про ідеальні зв'язки див. наступну главу). Вони характерні тим, що робота їхніх реакцій дорівнює нулю. У нашому випадку це означає, що робота вну-
158
трішніх сил дорівнює нулю:
Аi = 0. |
(148) |
Крім того, з умови випливає, що
Т0 = 0. |
(149) |
Для знаходження кінетичної енергії системи в кінцевому положенні необхідно з'ясувати, який рух виконує кожне з тіл.
Кривошип обертається навколо нерухомої осі, що проходить через точку О. Тому його кінетична енергія визначається за формулою
T (1) = |
J z(1)ω12 |
. |
|
2 |
|||
|
|
Оскільки кривошип являє собою стержень, то його момент інерції дорівнює
J z(1) = |
m l |
2 |
|
|
m |
(4R)2 |
|
|
16m R |
2 |
|
||
1 |
|
= |
|
|
1 |
|
|
= |
1 |
. |
|||
3 |
|
|
|
|
3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
3 |
|
|
|||
Тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T (1) |
|
|
8m R2 |
ω2 |
|
|
|
|
||||
|
= |
|
1 |
1 |
|
. |
(150) |
||||||
|
|
3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Швидкість центра колеса II можна виразити через кутову швидкість кривошипа, оскільки точка С2 є одночасно точкою кривошипа
VC2 = ω1 2R . |
(151) |
Колесо II котиться по нерухомому колесу I. Оскільки прослизання при цьому відсутнє, то швидкість точки D колеса II, що знаходиться в зіткненні з колесом I, дорівнює нулю: VD = 0. Це значить, що точка D є миттєвим центром швидкостей колеса II. Кутова швидкість колеса дорівнює:
ω2 = |
VC |
2 |
= 2ω1 . |
(152) |
|
R |
|||||
|
|
|
|||
Оскільки колесо виконує плоский рух, його кінетична енергія визначається за формулою
159
T (2) |
= |
|
m2VC2 |
+ |
JC(2)ω22 |
. |
(153) |
|||
|
2 |
2 |
|
|||||||
2 |
|
2 |
||||||||
|
|
|
|
|
|
|||||
Колесо є однорідним суцільним диском, тому |
|
|||||||||
|
J |
(2) = |
m2 R2 |
. |
|
|
(154) |
|||
|
|
|
|
|||||||
|
|
C2 |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Підставляючи (151), (152) і (154) у (153), будемо мати |
|
|||||||||
T (2) = 2m2ω12 R2 + m2ω12 R2 |
= 3m2ω12 R2 . |
(155) |
||||||||
Знайдемо швидкість |
точки Е колеса II. Оскільки миттєвий центр |
|||||||||
швидкостей знаходиться в |
|
точці D, то |
|
|
|
|||||
VE = ω2 2R = 4ω1R . |
|
(156) |
||||||||
Розглянемо тепер рух колеса III. Швидкість центра колеса |
||||||||||
дорівнює: |
|
|
|
|
|
|
|
|
|
|
VC3 = ω1 4R . |
|
|
(157) |
|||||||
Оскільки прослизання між колісьми II і III відсутнє, швидкість точки Е колеса III також визначається з (156). Зіставляючи формули (156) і (157), а також використовуючи наслідок із другої формули Эйлера для плоскопаралельного руху, дійдемо висновку, що колесо III виконує поступальний рух. Тому його кінетична енергія визначається за формулою
T |
(3) = |
m2VC23 |
= 8ω12 R2 . |
(158) |
|
||||
|
2 |
|
|
|
Складаючи Т(1), Т(2) і Т(3), одержуємо кінетичну енергію системи в
кінцевому положенні |
|
|
|
|
|
Т1 |
= ( |
8m1 |
+11m2 ) ω12 R2 . |
(159) |
|
3 |
|||||
|
|
|
|
Перейдемо до визначення роботи зовнішніх сил. Оскільки це сили ваги, то для обчислення роботи використовуємо формулу (126). Вага кривошипа і вага колеса II прикладені в точці С2 . Легко з'ясувати, що переміщення цієї точки вздовж вертикалі (див. мал.43) дорівнює
h2 = 2R .
Вага колеса III прикладена у точці С3 , переміщення якої по вертикалі дорівнює
160
