Курс теоретичної механіки 2007 (Укр)
.pdf
Г Л А В А II
НАЙПРОСТІШІ РУХИ ТВЕРДОГО ТІЛА
§ 1. Поступальний рух
Рух тіла називається поступальним, якщо будь-яка пряма, проведена в цьому тілі, залишається паралельної своєму первісному
положенню.
Теорема. При поступальному русі точки тіла описують однакові траєкторії (тобто які можуть бути суміщені) і в кожен момент часу точки тіла мають геометрично рівні швидкості і
геометрично рівні прискорення.
Доказ. Нехай при t = 0 тіло зайрисо положення I, а в момент часу t
– положення II (мал.17). Проведемо через дві точки А и В у початковому положенні тіла пряму (на кресленні вони позначені через Ао і Во). У процесі руху її напрямок залишається незмінним, оскільки вона залишається паралельною своєму первісному положенню. Крім того, довжина відрізка АВ залишається незмінною, оскільки точки А и В є точками абсолютно твердого тіла. Звідси випливає , що
|
|
|
|
|
|
|
|
|
Мал.17. |
|
AB = const |
(42) |
|||
|
|
|
Якщо перемістити |
точку |
А |
||
|
|
|
|
|
|||
на вектор AB , то вона суміщиться |
з точкою В. Оскільки |
це |
|||||
справедливо для будь-якого моменту часу, то при зсуві на вектор AB уся траєкторія точки А суміщиться з траєкторією точки В. Оскільки точки А и В – довільні точки тіла, то звідси випливає, що всі точки
тіла описують однакові траєкторії.
З креслення випливає, що |
|
rB = rA + AB . |
(43) |
71
Це рівність справедлива в будь-який момент часу, тобто в лівій і правій частинах її стоять рівні вектор-функції часу.
Диференціюючи (43) за t, одержимо
VB =VA , |
(44) |
оскільки d AB = 0 . Диференціюючи (44) ще раз за часом, приходимо dt
до наступної рівності:
aB = aA . |
(45) |
Оскільки А и В – довільні точки тіла, то можна зробити висновок, що в кожен момент часу точки тіла мають геометрично рівні
швидкості і геометрично рівні прискорення.
Наслідок. Поступальний рух тіла визначається рухом однієї
точки цього тіла.
Дійсно, точки тіла рухаються уздовж однакових траєкторій і через рівність швидкостей і прискорень у кожен момент часу вони рухаються однаково уздовж цих траєкторій.
Тому рівняння поступального руху тіла мають наступний вид:
xA = f1 (t), yA = f2 (t), z A = f3 (t) |
(46) |
де А – одна з точок тіла.
§ 2. Обертання тіла навколо нерухомої осі
Обертанням тіла навколо нерухомої осі називається такий рух
тіла, при якому принаймні дві точки тіла залишаються нерухомими (мал.18).
Пряма, що проходить через нерухомі точки, називається віссю обертання.
Двогранний кут між двома площинами, що проходять через вісь обертання, однієї – нерухомої, і іншої – рухливої, жорстко зв'язаної з тілом, узятий з урахуванням знака, називається кутовою координатою. Кутовій координаті φ приписується знак «плюс»,
якщо з додатнього напрямку, обраного на осі обертання, поворот на кут φ від нерухомої По до рухливої площини П видний проти
годинної стрілки, і знак « мінус» у протилежному випадку.
Кутова координата виміряється в радіанах.
72
Якщо задати кутову координату як функцію часу, то положення тіла буде визначено в будь-який момент часу. Тому
рівняння
φ = f ( t ), |
(47) |
називається рівнянням обертання твердого тіла навколо
нерухомої осі.
Нехай за деякий проміжок часу t кутова координата φ одержала збільшення Δφ. Відношення Δφ/Δt називається середньою кутовою
швидкістю тіла за проміжок часу t. Кутовою швидкістю тіла в момент часу t називається границя середньої кутової швидкості при t прагнучому до нуля:
ω = lim |
φ = |
dφ |
, |
|
|||
t→0 |
t dt |
||
тобто кутовою швидкістю обертання тіла навколо нерухомої осі
називається похідна кутової координати за часом.
Кутова швидкість виміряється в рад/сек. Аналогічно, кутовим прискоренням називається границя відносини збільшення кутової швидкості Δω до проміжку часу t
при t→0:
ε = lim |
ω |
= |
dω |
, |
|
|
|||
t→0 |
t dt |
|||
тобто кутовим прискоренням обертання
тіла навколо нерухомої осі називається
похідна кутової швидкості за часом.
Кутове прискорення виміряється в
рад/сек2.
Мал.18
§ 3. Деякі окремі випадки обертання тіла навколо нерухомої осі
1. Рівномірне обертання.
Обертання тіла називається рівномірним, якщо його кутова швидкість постійна, тобто
73
ω = dφ = const . dt
Звідси знаходимо, що dφ = ωdt і, інтегруючи, одержуємо
φ = ωt + φo |
(48) |
(φo – кутова координата обертового тіла при t = 0), тобто
закон рівномірного обертання тіла являє собою лінійну функцію
часу.
Визначимо кутове прискорення тіла
ε = dω = 0 , тобто dt
при рівномірному обертанні кутове прискорення тіла дорівнює нулю.
2.Рівнозмінное обертання тіла.
Рівнозмінным називається обертання тіла з постійним кутовим прискоренням, тобто
ε = dω = const dt
Звідси dω = εdt , і після інтегрування одержуємо
ω = εt + ωo |
(49) |
(ωоб – значення ω при t = 0).
Підставляючи ω = dφ в (49) і інтегруючи, знаходимо dt
φ = |
εt 2 |
+ ωot + φo . |
(50) |
|
2 |
||||
|
|
|
Таким чином, закон рівнозмінного обертання тіла являє собою
квадратичну функцію часу.
Якщо ε > 0, обертання тіла називається равноприскореним, якщо ж ε < 0, обертання тіла називається равноуповільним.
74
§ 4. Швидкості і прискорення точок обертового тіла
Точка М тіла, що обертається навколо нерухомої осі, рухається увздовж кола, центр якого С знаходиться на осі обертання(мал.19). Нехай відстань від точки до осі обертання, тобто радіус кола, увздовж якого рухається точка, дорівнює h. Позначимо через О точку перетинання кола з нерухомою площиною, а рухливу площину проведемо через радіус СМ. Тоді кут ОСМ буде дорівнює кутовій координаті φ, а положення точки М на колі можна задати за допомогою натуральної координати s, рівній довжині дуги кола ОМ. Якщо задане рівняння обертання тіла (47), то співвідношення
s = hφ
задає закон руху точки М по кола при натуральному способі завдання руху. Алгебраїчна величина швидкості визначається за формулою
|
|
|
Vτ = |
ds |
= h |
dφ |
= hω |
|
|
|||
|
|
|
dt |
|
|
|
||||||
|
|
|
|
|
|
dt |
|
|
|
|||
|
Дотичне і нормальне прискорення точки |
|||||||||||
|
знаходимо з формул |
|
|
|
||||||||
|
aτ = |
dVτ |
= h |
dω |
|
= hε, an = |
V 2 |
= hω |
2 |
|||
|
dt |
dt |
ρ |
|
||||||||
|
|
|
|
|
|
|
|
|||||
Мал.19 |
(оскільки для кола ρ = h ). Повне прискорення |
|||||||||||
|
точки визначаємо за формулою |
|
|
|||||||||
a = 
aτ2 + an2 = h
ε2 + ω4 .
Таким чином, формули
Vτ = hω, aτ = hε, an = hω2 , a = h ε2 + ω2 |
(51) |
визначають швидкість і прискорення точки тіла, що обертається навколо нерухомої осі.
§ 5. Перша формула Эйлера
Уведемо поняття кутової швидкості як вектора.
75
Вектором кутової швидкості тіла, що обертається навколо нерухомої осі, називається вектор, рівний за модулем абсолютній величині похідної кутової координати за часом і спрямований
уздовж осі обертання в той бік, відкіля видне обертання тіла навколо осі проти годинної стрілки (мал.20).
Теорема. Швидкість точки тіла, що обертається навколо нерухомої осі, дорівнює векторному добутку кутової швидкості тіла на радіус-вектор точки, проведений з полюса, що лежить на осі:
V = [ω, r] |
(52) |
(формула (52) і являє собою першу формулу Эйлера). |
|
Доказ. |
|
Величина вектора V визначається за формулою |
|
V =| ω|h, |
(53) |
а величина вектора [ω,r] обчислюється так: |
|
|[ω,r]|=|ω||r|sin α, |
(54) |
оскільки |ω|=|dφ/dt|. З трикутника ОМС знаходимо
|r|sin α = h.
Підставивши це в (54), одержимо
|[ω,r]|=|ω|h. (55)
З (53) і (55) випливає, що
V =|[ω,r]|. |
(56) |
Вектор V спрямований увздовж дотичній до Мал.20 кола, площина якої перпендикулярна осі, тому цей вектор перпендикулярний осі, а крім
того, перпендикулярний радіусу кола СМ. У такий спосіб вектор V перпендикулярний площини ОМС. Вектор [ω,r] перпендикулярний векторам, що перемножуються, тобто площини того ж трикутника ОМС. Це значить, що вектори V і [ω,r] паралельні один одному і, як неважко переконатися, спрямовані в одну сторону. З огляду на (56), дійдемо висновку, що перша формула Эйлера (52) вірна.
76
§ 6. Приклад рішення задачі на обертання тіл навколо нерухомої осі
На мал.21 зображений плоский механізм, що складається з двох зубцюватих коліс, що знаходяться в зачепленні, з радіусами R1 і R2 і з виступами, що мають радіуси r1 і r2 відповідно, а також вантажі, підвішені на мотузці, намотаної на виступ другого колеса. Задано закон обертання першого колеса
φ |
1 |
= 3t3 |
, радіуси коліс і |
|
|
|
виступів
Мал.21 R1=50 см, r1= 30 см, R2= 40 см, r2=20 см. Необхідно визначити
кутову швидкість колеса 1, швидкість точки А, що знаходиться на ободу виступу колеса 1, кутове прискорення колеса 2, а також прискорення точки В на ободу другого колеса і вантажу 3 при t=2 c.
Рішення. Знаходимо спочатку кутову швидкість і кутове
прискорення колеса 1: |
|
|
|
|||
ω1 |
= |
dφ1 |
= 9t 2 (c−1 ), ε1 |
= |
dω1 |
=18t (c−2 ) . |
|
|
|||||
|
|
dt |
|
dt |
||
При t=2з маємо ω1 = 36 с-1, ε1 =36 с-2. Швидкість точки А визначається за формулою
VA = ω1r1 = 36 30 = 1080 см/с.
Для того щоб знайти кутові швидкість і прискорення колеса 2 необхідно скористатися співвідношеннями
ω1 = R2 , ε1 = R2 .
ω2 R1 ε2 R1
Звідси одержуємо ω2 = ω1R1 / R2 = 36 50/ 40 = 45с-1,
ε2 = ε1R1 / R2 = 45 с-2.
Дотичне і нормальне прискорення точки В знаходимо з формул
77
aτ,B = ε2 R2 = 45 40 = 1800 см/с2,
an,B = ω22 R2 = 452 40 =81000 R2= 40 см/с2
Повне прискорення точки В дорівнює
aB = 
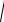aτ2,B + an2,B =81020 R2= 40 см/с2
Прискорення вантажу 3 дорівнює дотичному прискоренню точки С обода малого колеса 2:
a3 = aτ,C = ε2r2 = 45 20 = 900см / с2 .
78
Г Л А В А III
СКЛАДНИЙ РУХ ТОЧКИ
§ 1. Основні визначення
Рух точки називається складним, якщо він розглядається відносно декількох систем відліку, одна з яких вважається
нерухомої, а інші –тими, що рухаються відносно до неї.
Ми обмежимося розглядом випадку двох систем відліку (мал.22). На цьому малюнку xоyоzо – нерухома система відліку, xyz – рухлива система відліку, М – точка, що рухається. Кожна система відліку зв'язана з деяким тілом.
Тіло, з яким зв'язана рухлива система відліку, будемо
називати рухливим середовищем. Точка µ на мал.22 – це точ- Мал.22 ка рухливого середовища, з якою у даний момент часу збігається
точка М, що рухається.
Рух точки відносно нерухомої системи відліку називається абсолютним.
Рух точки відносно рухливої системи відліку називається відносним.
Рух рухливої системи відліку відносно нерухомої називається
переносним.
Визначення абсолютної, відносної і переносної швидкостей і відповідних прискорень зовсім аналогічні. Тому ці визначення суміщені. Відмінності у визначеннях прискорень поміщені в дужках.
Абсолютною швидкістю Va (абсолютним прискоренням aa) точки називається швидкість (прискорення) точки відносно нерухомої системи координат.
Відносною швидкістю Vr (відносним прискоренням ar) точки називається швидкість (прискорення) точки відносно рухливої системи координат.
79
Переносною швидкістю Ve (переносним прискоренням ae) точки, що рухається, називається швидкість (прискорення) тієї точки рухливого середовища, з яким у даний момент часу
збігається точка, що рухається.
Таким чином, переносна швидкість (переносне прискорення) точки М дорівнює швидкості (прискоренню) точки µ рухливого середовища відносно нерухомої системи відліку:
Ve =Vµ , ae = aµ .
§ 2. Теорема про додавання швидкостей
Абсолютна швидкість точки дорівнює геометричній сумі її відносної і переносної швидкостей, тобто
Va = Vr +Ve |
(57) |
Доказ.
Будемо називати абсолютною траєкторію точки відносно нерухомої системи відліку, а відносною – її траєкторію відносно
рухливої системи відліку (чи відносно рухливого середовища).
Розглянемо два положення рухливого середовища – у момент часу t і в момент часу t+ t (мал.23). Положення точки, що рухається, у момент часу t позначимо буквою М, а в момент часу t+Δt символом М/.
Нехай у момент часу t точка, що рухається, збігається з точкою µ рухливого середовища, а в момент t+ t – із точкою ν цього середовища. Крім того, позначимо через µ/ положення точки µ у момент t+ t. З мал.23 можна зробити висновок, що
Мал.23
MM / = µµ/ + µ / ν . |
(58) |
80