Курс теоретичної механіки 2007 (Укр)

(g прийнято рівним 9,8 м/с2).

Це і є диференціальне рівняння руху точки. Помноживши його на dt і інтегрируючи, одержимо

Значення постійної інтегрування З1 знайдемо з початкових умов (12), з огляду на те, що V = Vx = x& = 0 при t = 0. Підставляючи цю рівність у (16), знаходимо, що С1 = 0. Множачи тепер (16) на dt і інтегруючи ще раз, приходимо до наступного рівності:

Постійну інтегрування С2 знаходимо з умови х = 0 при t = 0. Підставляючи це в (17), знаходимо, що С2 = 0. Таким чином, рівняння руху тіла має наступний вид:

x = 16 t 4 − 0.49t 2 .

2.Прямолінійний рух точки під дією сили, що залежить від швидкості.

Задача. Деяке тіло масою m = 2 кг опускається усередині гладкої похилої труби, заповненою рідиною, без початкової швидкості (мал.4). Вважаючи, що сила опору рідини руху вантажу визначається співвідношенням R = 0,4V (Н) і зневажаючи силою рідини, що виштовхує, знайти швидкість тіла після 10 с з початку руху.

Рішення. Показуємо на кресленні Мал.4 сили, що діють на тіло, і складуємо

основне рівняння динаміки точки

111

Підставляючи сюди вихідні дані, одержуємо диференціальне рівняння:

dV = 4,9 − 0,2V . dt

Це рівняння з перемінними, що розділюються. Приводимо його до наступного виду:

Використовуємо початкову умову: V = 0 при t = 0. З (20) одержуємо

С = 5 ln 4,9.

Підставимо це в (20) і зробимо потенціювання:

З (21) випливає, що з часом V зростає від нуля поступово наближаючись до 24,5 м/с, але теоретично ні при якому кінцевому t цього значення не досягає. Тому знак абсолютної величини в (21) може бути опущений. У результаті одержуємо

Рівність (22) показує, що практично вже через кілька секунд після початку руху V невловимо мало відрізняється від свого граничного значення. При t =10 с V = 24,5 м/с.

3.Балістична задача.

Розглянемо рух тіла (снаряда), викинутого з початковою швидкістю Vo із точки О горизонтальної площини під кутом α до цієї площини. Опором повітря зневажаємо, крім того, будемо вважати, що сила ваги снаряда усюди та сама, тобто що висота польоту снаряда не

112

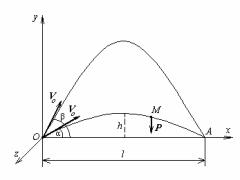
дуже велика. Необхідно при заданих α і Vo знайти дальність польоту снаряда l і час його польоту Т, а також при заданих Vo і l знайти кут пострілу α (тобто вирішити задачу прицілювання).

Рішення. Проведемо вертикальну площину через вектор Vo. У цій площині через точку проводимо горизонтальну вісь Ох і вертикальну вісь Оу. Вісь Оz проводимо перпендикулярно площини

Оху.

На снаряд, що ми вважаємо матеріальною точкою, діє тільки одна сила ваги. Тому основне рівняння динаміки виглядає так:

Vx = x&, Vy = y&, Vz = z& , приходимо до наступного диференціальним

C1 = Vo cos α, C2 = Vo sin α, C3 = 0. Тоді (25) запишеться так:

113

x& = Vo cos α, y& = Vo sin α− gt, z& = 0 .

Множачи ці рівності на dt і інтегруючи, знаходимо

x = Vo t cos α +C4, y = Vo t sin α − gt2 / 2 + C5, z = C6 . (27)

Підставляючи сюди значення x, y і z з перших трьох рівностей (26) і t= 0, одержуємо, що

С4 = С5 = С6 = 0.

При цих значеннях довільних постійних рівності (27) являють собою рівняння руху снаряда:

Остання рівність означає, що снаряд рухається в площині Оху.

1. Знайдемо рівняння траєкторії снаряда. Для цього необхідно виключити час t з перших двох рівнянь (28):

Таким чином, снаряд, випущений під кутом до обрію, при відсутності опору повітря рухається по параболі.

2.Визначимо горизонтальну дальність польоту снаряда.

Для цього в рівнянні (29) покладемо у = 0. Не співпадаюча з початком координат точка траєкторії з такою ординатою має абсцису

g

Визначимо час польоту снаряда. Для цього в першої рівності (28) покладемо х рівним правої частини (30). У результаті будемо мати

3.Залишилося вирішити задачу прицілювання. Помітимо, що з

(30)випливає , що максимальна дальність польоту снаряда досягається при α = 45о:

114

l< lmax у ту саму мету можна влучити, стріляючи по двох траєкторіях – настильної (α < 45ο) і навісний (β =90о − α > 45ο).

§5. Вільні коливання матеріальної точки

Відновлюєчою чи квазиупругой називається сила, постійно спрямована до нерухомого центра О и пропорційна відстані від матеріальної точки М до цього центра, тобто

( c – додатньа постійна).

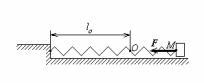
Подібна сила створюється розтягнутою чи стиснутою пружиною (мал.6).

Тут lo − довжина недеформованої пружини. При зсуві вантажу від точки О в будь-яку сторону пружина прагне повернути вантаж у вихідне положення, при цьому пружна сила пружини F пропорциональна величині зсуву

Мал.6 ОМ з коефіцієнтом пропорційності с, що носить назву коефіці-

єнта жорсткості пружини.

Прямолінійний рух матеріальної точки під дією тільки однієї відновлючої сили, називається вільними коливаннями Точка О

(центр відновлючої сили,) називається центром коливань.

Помітимо, що центр коливань є положенням рівноваги точки М. Дійсно, відповідно до формули (31), якщо матеріальна точка М знаходиться в положенні О, те F виявляється рівної нулю, і на точку М в цьому положенні взагалі не діють сили.

115

Проведемо вісь Ох з центра коливань уздовж прямої, по якій рухається точка (мал.7). Складемо основне рівняння динаміки точки

ma = F

і спроектуємо його на вісь х, з огляду на те, що проекція відновлючої сили, дорівнює

У результаті будемо мати

Розділивши (32) на m і ввівши позначення

m

одержуємо диференціальне рівняння вільних коливань матеріальної

точки

Це лінійне однорідне диференціальне уранение другого порядку з постійними коефіцієнтами. Складемо його характеристичне рівняння :

λ2 + k2 = 0.

Оскільки корені його чисто мнимі λ1,2 = ± ικ, то загальне рішення диференціального рівняння (34) має наступний вид:

x = C1 sin kt + C2 cos kt.

Зробимо підстановку C1 = a cos α, C2 = a sin α. У результаті

матеріальної точки.

Прямолінійний рух точки, чинений за законом x = a sin (kt + α),

називається гармонійними коливаннями.

116

Таким чином, вільні коливання матеріальної точки є

гармонійними.

Величина а, що є найбільшим відхиленням точки від центра

коливання, називається амплітудою.

Величина φ = kt + α називається фазою коливання, а α = φ (0)

називається початковою фазою.

Величина k називається круговою чи циклічною частотою

коливань.

Проміжок часу Т, протягом якого точка виконує одне повне

коливання, називається періодом коливань.

Це означає, що якщо час у формулі (35) збільшується на Т, то аргумент синуса в цій формулі змінюється на 2π. Звідси випливає, що k = 2π, тобто

тобто кругова частота дорівнює числу повних коливань, чинених за 2π одиниць часу.

Число ν повних коливань, чинених в одиницю часу, називається

частотою коливань:

117

1)амплітуда і початкова фаза коливань залежать від початкових умов,

2)кругова частота і період не залежать від них.

§6. Вплив постійної сили на вільні коливання матеріальної точки

Нехай тепер на матеріальну точку крім відновлючої сили, діє ще постійна сила Р (мал.8).

Знайдемо нове положення рівноваги О1 точки М. Очевидно, у цьому положенні F + P = 0, тобто

Знайдемо тепер геометричну суму сил, що діють на точку в довільному положенні:

F1 = F + P = −c OM + P . Підставивши сюди Р з (42), будемо мати

F1 = −c OM + c OO1 = −c O1M .

Це означає, що фактично точка рухається під дією відновлючої сили F1 , центр якої знаходиться в новому положенні рівноваги О1 , зміщеному на відстань δст від старого положення рівноваги. Звідси випливає справедливість усіх висновків попереднього параграфа й у цьому випадку. Таким чином,

додавання постійної сили не змінює характеру вільних коливань – вони залишаються гармонійними, але центр коливань зміщається

на величину статичного зсуву убік дії постійної сили.

З (33) і (44) маємо

k 2 = P .

mδст

118

Тоді

T = 2π = 2π m δст .

kP

Це означає, що період коливань пропорційний кореню квадратному

зі статичного зсуву.

Якщо сила Р є силою ваги, тобто коли коливання відбуваються по вертикальній прямій, то P = mg і

g

§7. Вільні коливання матеріальної точки при наявності в'язкого опору

Нехай тепер крім відновлючої сили, F на матеріальну точку діє сила опору R, пропорційна першого ступеня швидкості точки, тобто

Знак мінус у рівності (46) означає, що сила опору спрямована протилежно швидкості. Складемо основне рівняння динаміки

Мал.9

ma = F + R

і спроектуємо його на вісь х:

Розділимо (47) на m і в результаті одержимо диференціальне

рівняння вільних коливань матеріальної точки при наявності в'язкого опору

Тут β = b / 2m. Рівняння (48) – це лінійне однорідне диференціальне рівняння другого порядку з постійними коефіцієнтами. Складемо характеристичне рівняння:

119

Його корені мають наступний вид:

1. Розглянемо спочатку випадок малого опору β < k.

Уведемо позначення

Тоді корені характеристичного рівняння запишуться так:

λ1,2 = − β ± ik1 ,

тобто корені характеристичного рівняння є комплексними. Загальне рішення диференціального рівняння (49) у цьому випадку записується

так:

x = e− βt (C1 sin k1 t + C2 cos k1t).

Зробивши усередині дужок перетворення аналогічно §5, одержимо

причому величини а і α визначаються з початкових умов.

Коливання, що відбуваються за законом x = a e− βt sin (k1t + α),

називаються затухаючими, оскільки величина e− βt прагне до нуля з часом.

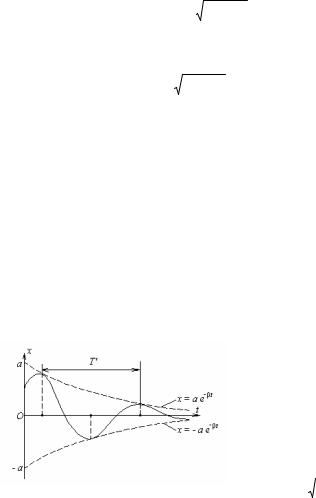
Графік функції (52) представлений на мал.10. Період функції sin (k1t + α) будемо називати періодом затухаю-

чих коливань:

e−βT '

Величина називається декрементом затухаючих коливань, а величина βT’ − логарифмічним декрементом.

120