
Курс теоретичної механіки 2007 (Укр)
.pdfкоординати у вираженні елементарної роботи діючих на систему сил.
Приклади.
1. Вільна матеріальна точка. Нехай на точку діє сила F.
Елементарна робота сили обчислюється за формулою
d = Fx dx + Fy dy + Fz dz.
Відповідно до приклада 1 попереднього параграфа q1 = x, q2 = y, q3 = z. Тоді
d = Fx dq1 + Fy dq2 + Fz dq3.
Зіставляючи цю рівність з (199), укладаємо
Q1 = Fx , Q2 = Fy , Q3 = Fz ,
тобто узагальнені сили дорівнюють проекціям сили, що діє на
точку, на осі координат.
Тіло, що має нерухому вісь обертання. Відповідно з формулою (131) §13 глави II частини III маємо
d = Mz dφ,
де Mz − сума моментів сил, що діють на тіло, відносно осі обертання. З огляду на те, що q1 = φ, робимо висновок, що узагальнена сила для
тіла, що обертається навколо нерухомої осі, є сума моментів сил, що діють на тіло, відносно осі обертання.
2. Плоска фігура, що рухається у своїй площині. У відповідності з формулою (133) (§13 глави II частини III) маємо
d = Mz dφ + (R , dΑ ), |
(200) |
n |
|
де M z = ∑mz (Fk ) , R − головний вектор |
плоскої системи сил |
k=1 |
|
{F1,F2,…,Fn}, діючих на фігуру, dΑ − вектор елементарного переміщення точки А.
Другий доданок у правій частині може бути записане так
181
(R , dА ) = Rx dxА +Ry dyА .
Підставляючи в (200), одержимо
d = Mz dφ + Rx dxА +Ry dyА .
Оскільки q1 = xА , q2 = yА , q3 = φ, то
n |
n |
|
Q1 = Rx = ∑npx Fk , Q2 = Ry = ∑npy Fk , |
|
|
k=1 |
k=1 |
(201) |
|
|
|
n
Q3 = M z = ∑mz (Fk ).
k=1
§12. Умови рівноваги в узагальнених силах
Теорема. Для того щоб механічна система, підлегла ідеальним, стаціонарним, геометричним, утримуючим зв'язкам, знаходилася в рівновазі, необхідно і досить, щоб всі узагальнені сили дорівнювали нулю:
Qi = 0 (I = 1,2,…,s). |
(202) |
Доказ. Відповідно до принципу можливих переміщень, необхідною і достатньою умовою рівноваги механічної системи, підлеглої ідеальним, стаціонарним, геометричним, утримуючим зв'язкам, є рівність
n |
|
δA = ∑(Fk , δrk ) = 0 , |
|
k=1 |
|
що відповідно до формули (199) може бути записана так |
|
s |
|
δA = ∑Qi δqi = 0. |
(203) |
i=1
Тут δqi − елементарне (нескінченно мале) збільшення узагальненої координати qi . Помітимо, що кожне таке збільшення надає системі можливе переміщення, оскільки воно відповідає накладеним зв'язкам.
182
Нехай система знаходиться в рівновазі. Надамо системі можливе переміщення, при якому δq1 ≠ 0, інші δqi = 0 (I = 2,3,…,s)... Тоді з (203) одержуємо
Q1 = 0.
Надамо тепер системі можливе переміщення, при якому δq2 ≠ 0, інші δqi = 0 (I = 1,3,…,s)... З (203) знаходимо
Q2 = 0.
Продовжуючи так само діяти і далі, одержимо
Qi = 0 (I = 3,4,…,s)...
Таким чином, з рівноваги системи випливає (202).
Допустимо тепер, що виконано рівності (202). Тоді з (203) випливає, що які б ні були δqi (I = 1,2,…,s),тобто яким б ні було можливе переміщення системи δА = 0 система знаходиться в рівновазі. Таким чином, з виконання рівності (202) випливає рівновага системи.
Теорема доведена.
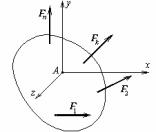
Приклад. Як приклад виведемо умови рівноваги плоскої системи сил. Плоска фігура знаходиться під дією системи сил {F1 , F2 , …, Fn}, лежачої в площині фігури. Проведемо осі х и у в цій площині, а вісь z перпендикулярно їй. Як показано в попередньому параграфі, узагальненими силами є наступні величини
|
|
n |
|
Q1 = Rx = ∑npx Fk , |
|
|
|
k=1 |
|
|
n |
|
Q2 = Ry = ∑npy Fk , |
|
|
|
k=1 |
|
|
n |
|
Q3 = M z = ∑mz (Fk ), |
|
|
|
k=1 |
|
дорівнюючи які нулю, одержуємо рівнян- |
|
Мал.60 |
ня рівноваги |
|
n |
n |
n |
∑npx Fk = 0, |
∑npy Fk = 0, |
∑mz (Fk ) = 0, |
k=1 |
k=1 |
k=1 |
183
співпадаючі з відомими рівняннями статики для плоскої системи сил.
§13. Рівняння Лагранжа
Як відзначалося в §6 дійсної глави додавання сил інерції Jk (k = 1,2,…,n)до сил Fk (k = 1,2,…,n),діючим на точки механічної системи, приводить до розширеної системи сил, що задовольняє умовам
рівноваги. Очевидно, узагальнені сили Qip (I = 1,2,…,s)розширеної системи сил задовольняють рівностям
Qip = Qi + Qiu ,
де Qi − узагальнені сили сил Fk (k = 1,2,…,n),а Qiu − узагальнені сили
інерції, що можуть бути знайдені перетворенням, аналогічним приведеному у §11:
|
n |
∂rk |
|
|
|
u |
= ∑(Jk , |
) (I = 1,2,…,s)... |
(204) |
||
Qi |
|
|
|||
∂q |
i |
||||
|
k=1 |
|
|
|
|
Якщо зв'язки, накладені на систему, є ідеальними, стаціонарними, геометричними й утримуючими, то відповідно до попереднього параграфа при русі системи повинні виконуватися наступні рівності:
Q |
i |
+ Qu = 0 (I = 1,2,…,s)... |
(205) |
|
i |
|
Сили інерції точок механічної системи визначаються рівностями
|
|
|
|
|
J |
|
= −m |
|
a |
|
= −m |
|
|
dVk |
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
k |
k |
k |
k |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Підставивши їх у (204), будемо мати |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
dVk |
|
|
∂rk |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
− Qiu |
= ∑mk |
( |
|
, |
|
) . |
|
|
|
|
|
|
|
(206) |
||||||||||||||||||||
|
|
|
|
|
dt |
|
∂qi |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Неважко переконатися в тім, що |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
( |
dVk |
, |
∂rk |
) = |
d |
|
(V |
|
, |
∂rk |
) |
− (V |
|
|
, |
d |
( |
∂rk |
)) . |
(207) |
|||||||||||||||||||
|
|
|
|
k |
|
|
k |
|
|
||||||||||||||||||||||||||||||
|
|
dt |
∂q |
|
dt |
|
|
|
|
|
∂q |
i |
|
|
|
|
|
|
|
|
dt |
|
∂q |
i |
|
|
|
||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Користаючись правилом Лопиталя, знаходимо |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
∂r |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
r& |
|
|
|
|
∂r& |
|
|
∂V |
k |
|
|
||||||||
|
|
k |
= |
lim |
|
k |
|
= |
|
lim |
|
|
|
|
k |
|
= |
|
|
|
k |
= |
|
|
|
. |
(208) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
∂qi |
|
q |
→0 |
|
qi |
|
|
|
|
q →0 |
|
|
& |
|
|
|
|
& |
|
|
|
& |
|
|
|
|||||||||||||
|
|
i |
|
|
|
|
|
& |
i |
|
|
|
qi |
|
|
|
|
∂qi |
|
|
∂qi |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Помітимо, що в результаті перестановки порядку диференціювання можна одержати наступну рівність
d |
( |
∂rk |
) = |
∂ |
( |
drk |
) = |
∂Vk |
. |
(209) |
|
|
|
|
|
||||||
dt |
∂qi |
∂qi dt |
∂qi |
|
||||||
184
Підставивши (208) і (209) у (207), одержуємо |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
( |
dVk |
, |
|
∂rk |
) = |
d |
(V |
|
, |
|
∂Vk |
|
|
) − (V |
|
, |
∂Vk |
) . |
(210) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dt ∂qi |
|
dt |
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
∂qi |
|
|
||||||||||||||||||||||
Помітимо |
|
|
|
|
|
|
|
(I |
|
∂qi |
|
|
|
|
|
|
|
|
|
|
|
|
|
узагальненими |
||||||||||||||||||||||||||||
|
попутно, |
|
що |
|
qi |
|
|
= 1,2,…,s)звуться |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
швидкостями. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по qi і qi дає |
|||||||||||||||||
Диференціювання квадрата швидкості Vk |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
||
|
|
|
|
∂V |
2 |
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂V |
k |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
k |
= |
|
|
|
|
|
|
|
(V |
|
,V |
|
) = |
|
2(V |
|
, |
|
|
|
), |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
∂q |
|
k |
k |
k |
∂q |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
∂q |
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
∂V |
2 |
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂V |
k |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
k |
= |
|
|
|
|
|
|
|
(V |
|
,V |
|
) = |
|
2(V |
|
, |
|
|
|
). |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
& |
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
∂qi |
|
|
∂qi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂qi |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
У результаті підстановки їх у (210) будемо мати |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dV |
k |
|
|
|
|
∂r |
|
|
d |
|
|
1 |
|
∂V 2 |
|
|
|
|
1 ∂V |
|
2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
( |
|
|
|
, |
|
|
|
k |
) = |
|
|
( |
|
|
|
|
|
k |
|
) − |
|
|
|
|
|
|
|
|
k |
. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ∂qi |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dt ∂qi |
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
dt 2 ∂qi |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Залишається підставити це вираження в (206): |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
∂ |
|
n |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
∂ |
|
|
|
n |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
∂T |
|
∂T |
|
|||||||
− Qiu = |
d |
( |
|
|
∑ |
mkVk |
) − |
|
|
|
∑ |
mkVk |
|
|
= |
d |
( |
|
) − |
. (211) |
||||||||||||||||||||||||||||||||
|
|
& |
|
|
|
|
|
|
|
|
|
|
& |
|
||||||||||||||||||||||||||||||||||||||
|
dt |
∂qi k=1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
∂qi k=1 |
|
2 |
|
|
|
|
|
|
|
dt |
|
|
∂qi |
∂qi |
|||||||||||||||||||||||
(Т – кінетична енергія механічної системи).
Зобліком (211) рівності (205) приймають наступний вид:
d |
( |
∂T |
) − |
∂T |
= Q |
|
(I = 1,2,…,s). |
(212) |
|
|
|
i |
|||||
dt |
& |
|
∂qi |
|
|
|||
∂qi |
|
|
|
|||||
Ці рівняння являють собою диференціальні рівняння руху
механічної системи в узагальнених координатах або рівняння Лагранжа.
§14. Приклад рішення задачі з застосуванням рівнянь Лагранжа
Задача. Механічна система (мал.61) складається з двох вантажів 1 і 2 однакової маси т1 і трьох блоків 3,4 і 5 однакової маси т2 і радіуса r, один із яких рухливий, а інші нерухомі. Через блоки перекинена мотузка так, як показано на малюнку. До одного кінця її прикріплений вантаж 1, а до іншого вантаж 2. Знайти прискорення вантажів ,
185
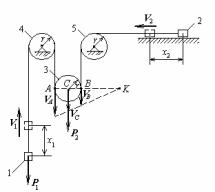
зневажаючи вагою мотузки і тертям на осях. Система починає рух зі стану спокою.
Рішення. Розглянута механічна система має дві ступені волі. Виберемо як узагальнені координати зсуву х1 і х2 вантажів 1 і 2 з початкового положення. Тоді рівняння Лагранжа будуть мати вид
|
|
d |
( |
∂T |
) − |
|
∂T |
= Q |
, |
||
|
|
|
|
|
|
||||||
|
|
dt |
|
& |
|
|
∂x1 |
1 |
|
||
|
|
|
∂x1 |
|
|
|
(213) |
||||
|
|
d |
|
∂T |
|
|
|
∂T |
|
||
|
|
( |
|
) − |
|
= Q2 . |
|||||
|
|
|
|
|
|
|
|
||||
|
|
dt |
& |
|
|
∂x2 |
|||||
|
|
|
∂x2 |
|
|
|
|
|
|||
|
Знайдемо узагальнені сили Qj |
||||||||||
|
(j =1,2). Надаємо спочатку |
||||||||||
|
механічній |
|
системі |
можливе |
|||||||
|
переміщення, при якому х1 |
||||||||||
|
одержує збільшення δх1, тобто |
||||||||||
|
вантаж 1 переміщається нагору |
||||||||||
незмін- |
на δх1, |
а |
х2 залишається |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Мал.61 |
ним, тобто вантаж 2 |
залиша- |
|||||||||
|
ється на місці. При цьому |
||||||||||
точка А рухливого блоку переміщається вниз на δх1 , а точка В залишається на місці. Тому точка С переміщається вниз на δх1/2 . Робота активних сил на цьому переміщенні дорівнює
δA1 = − Р1 δх1 |
+ |
P2δx1 |
= ( |
m2 |
− m )gδx . |
|||
|
|
|
||||||
|
2 |
2 |
1 |
1 |
||||
|
|
|
||||||
Тому |
|
|
|
|
|
|
|
|
Q1 |
= ( |
m2 |
− m )g . |
|
(214) |
|||
|
|
|||||||
|
2 |
1 |
|
|
|
|||
|
|
|
|
|
|
|||
Надаємо тепер системі інше переміщення, при |
якому х1 |
залишається незмінним (тобто вантаж 1 залишається на |
місці), а х2 |
одержує збільшення δх2 , тобто вантаж 2 переміщається вліво на δх2 . |
|
При цьому точка В рухливого блоку переміщається вниз на δх2 , а |
|
точка А залишається на місці. Тому |
точка З переміщається вниз на |
|||
δх2/2 . Робота активних сил на цьому переміщенні дорівнює |
||||
δA2 = |
P2δx2 |
= |
m2 |
gδx2 . |
|
|
|||
2 |
2 |
|
||
Тому
186
Q2 = |
m2 |
g . |
(215) |
|
2 |
||||
|
|
|
||
Кінетична енергія системи |
дорівнює сумі кінетичних энергій |
|||
тіл, що складають систему
Т = Т1 + Т2 + Т3 + Т4 + Т5 .
Тут Т1 і Т2 − кінетичні енергії вантажів, Т3 , Т4 і Т5 − кінетичні енергії блоків.
Припустимо, що вантаж 1 переміщається нагору зі швидкістю V1 , а вантаж 2 − уліво зі швидкістю V2. Кінетична енергія вантажів визначається за формулою
|
|
|
|
m V |
2 |
|
|
|
|
T |
|
|
= |
1 |
j |
|
( j =1,2) , |
|
|
j |
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|||
причому Vj = x j , тобто |
|
|
|
|
|
|
|||
& |
|
|
|
|
|
|
|
|
|
|
|
|
& 2 |
|
|
|
|||
T |
|
= |
m1x j |
|
( j = 1,2) , |
(216) |
|||
j |
|
|
|||||||
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|||
Рухливий блок виконує плоскопараллельное рух. Його кінетична енергія визначається за формулою (144)
|
m |
V |
2 |
|
J |
z |
ω2 |
|
|
T = |
2 |
|
C |
+ |
|
3 |
. |
(217) |
|
|
|
|
|
|
|
||||
3 |
2 |
|
|
|
2 |
|
|
||
|
|
|
|
|
|
||||
Тут VC − швидкість центра C блоку, ω3 − його кутова швидкість, момент інерції Jz визначається за формулою
J = |
m2 r 2 |
. |
(218) |
z |
2 |
|
Позначимо через А и В точкі обода блоку, що лежать на одному горизонтальному діаметрі. Точки А, В і С лежать на одній прямій, а отже, їхні швидкості змінюються згідно лінійному закону (§5 глави IV частини II), тобто
VA |
= |
VB |
= |
VC |
= ω |
3 |
, |
(219) |
|
|
|
||||||
AK |
|
BK |
|
CK |
|
|
||
|
|
|
|
|
||||
де K − миттєвий центр швидкостей блоку.
Згідно відомій властивості пропорції з (219) випливає
|
VA +VB |
= |
VC |
, |
|
AK + BK |
|
||
|
|
CK |
||
але AK +BK = 2CK. Тому |
|
|
|
|
187

VC = VA +VB . 2
Очевидно, VA = V1 = x&1 , VB = V2 = x&2 . Отже,
VC = x&1 + x&2 . 2
Аналогічно одержуємо з (219)
VA −VB = ω3 , AK − BK
але AK− BK = 2r. Отже,
ω3 = x&1 − x&2 .
2r
Підставляючи (218), (220) і (221) у (217), будемо мати
(220)
(221)
& |
& |
|
|
2 |
|
|
|
|
m2 r |
2 |
|
|
& |
|
|
|
|
& |
|
|
2 |
|
|
|
|
|
|
|
& 2 |
|
& 2 |
|
|
|
& & |
|
|
|||||||||||||||
T = |
m2 (x1 |
+ x2 ) |
|
|
+ |
|
|
(x1 |
− x2 ) |
|
|
= |
m2 (3x1 |
+ 3x2 |
+ 2x1x2 ) |
. |
(222) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16r |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Кінетична енергія нерухомих блоків визначається за формулою |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
= |
|
|
|
|
z |
|
|
j |
|
( j = 4,5) . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Кутові швидкості блоків рівні |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V1 |
|
|
|
|
& |
|
|
|
|
|
|
|
|
V2 |
|
& |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
ω |
4 |
= |
= |
x1 |
|
, ω |
5 |
= |
|
|
= |
|
x2 |
. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
r |
|
|
|
|
|
|
|
r |
|
|
r |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Тоді |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
2 |
|
|
|
|
|
|
& 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
4 |
= |
m2 x1 |
|
, T |
|
= |
m2 x2 |
. |
|
|
|
|
|
|
|
|
|
(223) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
5 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким чином, кінетична енергія системs визначається так |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
& 2 |
|
|
|
|
|
& |
2 |
|
|
|
|
|
|
|
|
|
|
|
& |
|
2 |
|
|
|
& |
2 |
|
& & |
|
|
|
|
|
|
& 2 |
& |
2 |
|
|||||||||||
T = |
m1x1 |
+ |
|
m1x |
2 |
+ |
m2 (3x1 |
+ 3x |
2 |
+ 2x1x2 ) |
+ |
m2 x1 |
|
+ |
m2 x |
2 |
, тобто |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
||||||||||||||
|
|
|
|
|
|
m1 |
|
|
& 2 |
|
|
|
& |
2 |
|
|
|
|
|
|
|
|
|
|
& |
2 |
& |
2 |
|
|
|
& & |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 (7x1 |
+ 7x |
2 + |
|
2x1x2 ) |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
T = |
|
|
|
|
|
(x1 |
|
+ x |
2 ) + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
(224) |
||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
З (224) знаходимо
188
∂T |
|
|
|
∂T |
|
& |
|
m2 |
(7x1 |
+ x2 ) |
|
|
= 0 ( j = 1,2), |
|
|
= m1x1 |
+ |
|
& |
& |
, |
||
∂x j |
& |
|
8 |
|
|||||||
& m2 |
|
∂x1 |
+ x1 ) |
|
|
|
|
|
|||
∂T |
(7x2 |
|
|
|
|
|
|
||||
|
= m1x2 + |
|
& |
& |
. |
|
|
|
|
|
|
& |
|
8 |
|
|
|
|
|
|
|||
∂x2 |
|
|
|
|
|
|
|
|
|
||
Підставляючи (214), (215) і (225) у (213), одержуємо
|
|
|
|
|
m |
2 |
|
(7 |
&x& |
|
+ &x& |
) |
|
|
|
|
m |
2 |
|
|
|
|
|
|
|||||||
|
m |
&x& |
+ |
|
|
|
|
|
1 |
|
2 |
|
|
= |
( |
|
|
− m )g, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
m |
2 |
(7&x& |
|
+ &x& |
|
) |
|
|
|
m |
2 |
|
|
|
|
|
|
|
|||||||
|
m |
&x& |
+ |
|
|
|
|
|
2 |
1 |
|
|
= |
|
|
|
g, |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
відкіля знаходимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m + |
3 |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11m2 |
|
|||||||||||||||
&x& |
= − |
|
1 |
|
|
|
8 |
|
|
2 |
|
g, &x& |
|
|
= |
|
|
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
|
|
|
7 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|||
|
|
|
m + |
|
m |
|
|
|
|
|
|
|
|
8(m |
+ |
m |
|
) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|||||||||||||||||||
|
|
|
|
1 |
|
|
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|||
Це і є прискорення вантажів. Знак «мінус» при вантаж 1 рухається вниз, а не нагору, як передбачалося.
(225)
(226)
&x&1 означає, що
189
Література, що рекомендується
1.Айзенберг Т.Б., Воронков И.М., Осецький В.М. Керівництво до рішення задач з теоретичної механіки. - М.: Высш. шк., 1961.
2.Бать М.І., Джанелідзе Г.Ю., Кельзон А.С. Теоретична меха-
ніка в прикладах і задачах (у 3 т.). − М.: Наука, 1972 ( 1973.
3.Березова О.А., Солодовніков Р.В., Друшляк Г.Ю. Збірник задач з теоретичної механіки. − К.: Вища школа, 1975.
4.Бутенін Н.В., Лунц Я.Л., Меркін Д.Р. Курс теоретичної ме-
ханіки (у 2 т.). − М.: Наука, 1979.
5.Бухгольц Н.Н. Основний курс теоретичної механіки (у 2ч.) –
М.: Наука, 1972.
6.Голубєв Ю.Ф. Основи теоретичної механіки.- М.: Изд. МГУ,
1992.
7.Кільчевський Н.А. Курс теоретичної механіки (у 2 т.). - М.: Наука, 1972-1977.
8.Кирилов В.Х., Д.Д. Лещенко. Курс теоретичної механіки.
-Одеса: Вид-во ОДАБА, 2002.
9.Кошляков В.Н. Короткий курс теоретичної механіки. Кінематика, кінетика.- К.: Вища шк., 1993.
10.Лойцянський Л.Г., Лур'є А.И.. Курс теоретичної механіки (у 2 т.). - М.: Наука, 1982.
11.Маркеєв А.П. Теоретична механіка. - М.: Наука, 1990.
12.Нікітін Н.Н. Курс теоретичної механіки. - М.: Высш. шк.,
1990.
13.Павловський М.А., Акінфієва Л.Ю., Бойчук О.Ф. Теоретична механіка. Статіка. Кінематика. - К.: Вища шк., 1989.
14.Павловський М.А., Акінфіева Л.Ю., Бойчук О.Ф. Теоретична механіка. Динаміка. - К.: Вища шк., 1990.
15.Павловський М.А., Путята Є.В. Теоретична механіка. - К.: Рад. шк., 1985.
16.Путята Т.В., Фрадлін Б.Н. Методика розв'язування задач з теоретичної механіки. - К.: Рад. шк., 1952.
17.Старжинський В.М. Теоретична механіка: короткий курс по повній програмі вузів. - М.: Наука, 1989.
18.Яблонський А.А., Нікіфорова В.М. Курс теретичної механіки. ч.1. Статіка. Кінематика. - М.: Высш. шк., 1977.
19.Яблонський А.А. Курс теретичної механіки.( ч.2. Динаміка. - М.: Высш. шк., 1977.
190
