
Курс теоретичної механіки 2007 (Укр)
.pdf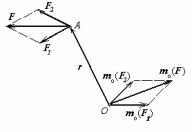
вектора [r,F] побудуємо вектор F/ = F, що виходить із точки О. За визначенням векторного добутку вектор [r,F] = [r,F/] повинний бути перпендикулярний площини, що проходить через вектора r і F/. Але ця площина збігається з площиною, що проходить через r і F, тобто mo(F) і [r, F] перпендикулярні однієї і тієї ж площини, тобто спрямовані уздовж однієї і тієї ж прямої (мал.10). Крім того, [r,F] спрямований у ту сторону, відкіля видний поворот від вектора r до вектора F/ на кут α проти годинної стрілки. Але з цієї ж сторони видно, що сила F створює обертання навколо полюса О проти годинної стрілки, тобто mo(F) і [r,F] мають те саме напрямок. З урахуванням рівності (4) одержуємо, що (1) справедливо.
§ 6. Теорема Вариньона для моментів двох сил, що сходяться, відносно полюса
Якщо дві сили F1 і F2, а також сила F, яка дорівнює їхній геометричній сумі, прикладені в одній точці (мал.11), то момент
цієї сили відносно будь-якого полюса дорівнює геометричній сумі
моментів сил F1 і F2 відносно того ж полюса.
Доказ. Момент сили F відповідно до викладеного в попередньому параграфі може бути представлений у наступному виді:
mo (F) = [r, F]
(r – радіус-вектор точки А). Але |
F1+F2 = F, і підставляючи цю |
рівність у попередню, одержуємо |
|
mo (F) = [r, F1 ]+[r, F2 ]
Але |
[r , F1] = mo (F1), |
а |
[r , |
F2]= = mo (F2) (тому що F1 |
і |
F2 |
|
також прикладені в точці А). Таким чином, одержуємо
mo (F) = mo (F1 ) + mo (F2 )
(що і було потрібно довести).
Мал.11
11
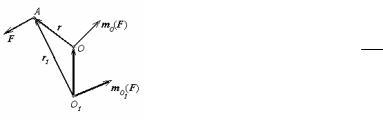
§ 7. Зміна моменту сили відносно полюса при зміні полюса
Задано силу F і два полюси, О (який будемо називати старим) і О1 (який будемо називати новим) (Мал.12). Знайдемо залежність між моментами сили відносно цих полюсів. Користаючись представленням моменту у виді векторного добутку,
можемо записати
mo (F) = [r1, F] . |
(5) |
1 |
|
Очевидно (див. мал.), що r1 = O1O + r . Підставляючи це в (5) і з огляду на, що
mo (F) = [r, F] ,
Мал.12 одержуємо
|
|
|
|
mo (F) = mo (F) +[O1O, F] , |
(6) |
||
1 |
|
|
|
тобто доведена
Теорема. Момент сили відносно нового полюса дорівнює моменту сили відносно старого полюса, геометрично складеному з векторним добутком вектора, що з'єднує новий полюс зі старим, на силу.
§ 8. Залежність між моментом сили відносно полюса і моментом сили відносно осі
Теорема. Момент сили відносно осі, що проходить через полюс,
дорівнює проекції на цю вісь моменту сили відносно полюса.
Доказ. Модуль моменту сили відносно полюса дорівнює:
| mo (F) |= Fh = 2S OAB . |
(7) |
Абсолютна величина моменту сили відносно осі дорівнює: |
|
| mz (F) |= F' h1 = 2S OCD . |
(8) |
Методами елементарної геометрії можна довести, що |
|
12
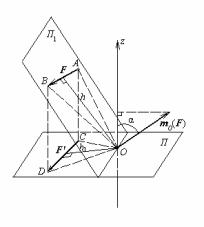
S OCD = S OAB cosα , |
(9) |
де α – кут між перпендикулярами до площин Π і Π1, у яких розташовані трикутники. З (7) –
(9) випливає, що
| mz (F) |=| mo (F) | cos α . (10)
|
У ситуації, зображеної на |
|
мал.13, знаки прzmo(F) і mz(F) |
|
збігаються. Легко переконатися, |
|
що й в інших випадках їхні знаки |
|
однакові. |
|
З огляду на (10), можемо |
|
записати |
|
mz (F) = прz mo (F) (11) |
Мал.13 |
(що і було потрібно довести). |
§ 9. Теорема Вариньона для моментів двох сил, що сходяться, відносно осі
Якщо дві сили F1 і F2, а також сила F, яка дорівнює їхній
геометричній сумі, прикладені в одній точці, то момент цієї сили відносно будь-якої осі дорівнює сумі моментів сил F1 і F2 відносно
тієї ж осі.
Доказ. Записуємо теорему Вариньона для моментів сил відносно полюса
mo (F) = mo (F1 ) + mo (F2 )
іпроектуємо цю векторну рівність на вісь z. Використовуючи зв'язок між моментами відносно полюса й осі, одержуємо
mz (F) = mz (F1 ) + mz (F2 ) (що і було потрібно).
§ 10. Система сил. Головний вектор і головний момент системи сил
Системою сил S{F1,F2,…,Fn}називається сукупність сил, прик-
13

ладених до одного твердого тіла.
Головним вектором R системи сил називається вільний вектор, який дорівнює геометричній сумі сил, що входять у систему:
n
R = ∑Fk .
k=1
Головним моментом Мо системи сил відносно полюса О називається вектор, прикладений у цьому полюсі і рівний геометричній сумі моментів сил системи відносно цього полюса:
|
n |
|
|
Mo = ∑mo (Fk ) . |
|
|
k=1 |
|
|
Помітимо, що з формули (11) випливає, що |
|
|
прz Mo =Mz , |
(12) |
|
n |
|
|
де M z = ∑mz (Fk ) , тобто сума моментів |
|
|
k=1 |
|
Мал.14 |
сил відносно осі z (Мz будемо називати го- |
|
ловним моментом системи сил відносно |
||
осі z).
Таким чином, головний момент системи сил відносно осі
дорівнює проекції на цю вісь головного моменту системи сил відносно полюса, що лежить на цій осі.
§ 11. Зміна головного моменту системи сил відносно полюса при зміні полюса
Теорема. Головний момент системи сил відносно нового полюса O1 дорівнює головному моменту системи сил відносно старого полюса O, складеному з векторним добутком вектора, що
з'єднує новий полюс зі старим, на головний вектор системи сил, тобто
|
|
|
|
Mo = Mo +[O1O, R] . |
(13) |
||
1 |
|
|
|
Доказ. Для кожної сили, що входить у систему, можна записати теорему про зміну її моменту при зміні полюса
mo1 (Fk ) = mo (Fk ) +[O1O, Fk ] (k = 1,2,..., n) .
14
Підсумовуючи всі ці рівності по k і виносячи загальний множник O1O за знак суми, одержуємо
n
Mo1 = Mo +[O1O, ∑Fk ]
k=1
що збігається з (13).
Наслідок. Якщо головний вектор системи сил дорівнює нулю, то її головний момент не залежить від полюса, тобто є вільним вектором.
Доказ. Якщо R = 0, то з (13) випливає Mo1 = Mo , чим і завершується доказ, тому що O1 і О два довільних полюси.
§ 12. Пара сил і її момент
Парою сил називається система з двох сил, що лежать на паралельних прямих, спрямованих у протилежні сторони і рівнихза величиною. Відстань між лініями дії сил пари називається плечем
пари. Воно передбачається обов'язково відмінним від нуля.
Сили, що утворяють пару, задовольняють співвідношенню F1 = - F2.
Тоді головний вектор пари сил:
R = F1 + F2 = 0
За наслідком з попереднього параграфа головний момент пари сил (іменований просто моментом пари сил) не залежить від полюса, тому мо-
Мал.15 же бути обчислений у будь-якому з них:
M = mB (F1 ) , |
(14) |
тому що mB (F2 ) = 0 . З (14) випливає | M |= F1h (до речі, звідси випливає, що М не дорівнює нулю, тому що h ≠ 0). З огляду на напрямок вектора mB (F1 ) , можна зробити наступний висновок:
момент пари сил – це нерівний нулю вільний вектор,
15
а) перпендикулярний площині пари, б) спрямований у ту сторону, відкіля видно, що пара сил
створює обертання проти годинної стрілки, в) рівний за величиною добутку величини однієї із сил паиа на
плече пари.
Якщо скористатися формулою (12), то можна прийти до наступного висновку:
момент пари сил відносно будь-якої осі, перпендикулярної площини пара, має одне і теж значення, рівне модулю моменту пари і маюче знак, обумовлений за наступним правилом:
якщо з додатнього напрямку осі видно, що пара створює обертання проти годинної стрілки, то приймається знак «плюс», у протилежному випадку приймається знак «мінус».
§ 13. Елементарні операції
Елементарними називаються наступні операції над системами сил:
1)додавання до системи сил двох прямопротилежних сил
(див. §4),
2)відкидання від системи сил двох прямопротилежних сил (якщо такі маються),
3)заміна двох сил, прикладених в одній точці, однією силою, рівною їхній геометричній сумі і прикладеної в тій же точці (тобто по «правилу паралелограма»).
Властивості.
1)Перенос сили уздовж її лінії дії можна виконати за
допомогою елементарних операцій. |
|
|
Доказ. Додамо до сили F у |
|
точці В, куди ми бажаємо пе- |
|
ренести силу, дві прямопро- |
|
тилежні сили F1 і F2, причому |
Мал.16 |
F1 = F, а F2 = - F. |
Одержуємо систему з трьох |
|
|
сил, з яких F і F2 також є пря- |
мопротилежними. Відкинемо їх, вико-ристовуючи другу елементарну операцію. У результаті залишиться тільки сила F1, рівна силі F і прикладена в точці В.
2. Розкладання сили на дві складові за правилом паралелогра-
16
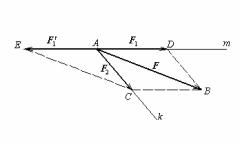
можна здійснити за допомогою елементарних операцій.
Доказ. Відкладемо від довільної точки А відрізок АВ, що зображує силу F у деякому масштабі. Нехай задані напрямки Ak і Аm, уздовж яких необхідно розкласти силу F на складові. Побудуємо паралелограм ACBD з діагоналлю АВ і сторонами AC і AD, що лежать на Ak і Am. Використовуємо тепер першу елементарну
операцію: додамо силу F1, рівну в обраному масштабі відрізку AD, і прямопротилежну їй силу
F1/ .
Позначимо кінець сили F1/ буквою Е. Неважко
переконатися в тім, що AECB також є паралело-
Мал.17 грамом.
Використовуємо тепер третю елементарну операцію: замінимо сили F і F1/ силою F2, що
збігається в обраному масштабі з відрізком АС. У результаті побудов одержуємо сили F1 і F2, спрямовані уздовж напрямків Ak і Am, сума яких дорівнює силі F.
Наслідок. Якщо система сил S2 отримана із системи сил S1 за допомогою елементарних операцій, то систему сил S1 можна
одержати з S2 також за допомогою елементарних операцій.
Доказ. Справді, перші дві елементарні операції є зворотними одна одної. Звертанням же третьої елементарної операції, як показує властивість 2, є деяка сукупність елементарних операцій.
§ 14. Геометричні властивості елементарних операцій
Перша геометрична властивість. Елементарні операції не
змінюють головного вектора системи сил.
Доказ. Перші дві елементарні операції не змінюють головного вектора системи сил, оскільки при цьому додаються чи відкидаються сили, геометрична сума яких дорівнює нулю. При використанні третьої елементарної операції дві сили заміняються однією, рівною їхній геометричній сумі. Отже, загальна геометрична сума сил, тобто їхній головний вектор, залишається незмінним.
17
Друга геометрична властивість. Елементарні операції не
змінюють головного моменту системи сил.
Доказ. Перші дві елементарні операції не змінюють головного моменту системи сил, тому що при цьому додаються чи відкидаються сили, сума моментів яких відносно будь-якого полюса дорівнює нулю (див. §4). При використанні третьої елементарної операції дві сили заміняються однією, момент якої відносно будь-якого полюса дорівнює геометричній сумі їхніх моментів (див. §6). Отже, загальна геометрична сума моментів відносно будь-якого полюса, тобто їхній головний момент, залишається незмінної.
§ 15. Еквівалентні системи сил
Системи сил S1 і S2 називаються еквівалентними (символічний запис S1 ~ S2), якщо одна з них може бути отримана з іншої за
допомогою елементарних операцій.
Помітимо, що в цьому визначенні використовується наслідок з §13, що дозволяє не вказувати в якому напрямку здійснювався перехід від однієї системи до іншої за допомогою елементарних операцій
Властивості.
1.Якщо S1 ~ S2, то S2 ~ S1.
2.Якщо S1 ~ S2, а S2 ~ S3, то S1 ~ S3.
Користаючись властивістю 1, ця властивість можна записати ще так
Якщо S1 ~ S2 і S3 ~ S2, то S1 ~ S3, тобто
Якщо кожна з двох систем сил еквівалентна третьої, то вони еквівалентні одна одної.
3. Якщо S1 ~ S2, то головні вектори цих систем сил і головні
моменти відносно того самого полюса геометрично рівні, тобто
R (S1) = R (S2) і Мо (S1) = Мо (S2).
Доказ випливає з геометричних властивостей елементарних операцій.
§ 16. Рівнодіюча
Якщо система сил S еквівалентна одній силі, то ця сила
називається її рівнодіючої.
Властивості.
1.Рівнодіюча геометрично дорівнює головному вектору.
18

Доказ. Позначимо систему сил, що складається з одної рівнодіючої F, символом S1. Тоді з визначення рівнодіючої випливає, що S ~ S1, і з властивості 3 попереднього параграфи одержуємо, що R(S) = R(S1), і оскільки система S1 складається з однієї сили F, те R(S1) = F. Таким чином, R(S) = F.
2. (Узагальнена теорема Вариньона). Якщо система сил має рівнодіючу, то момент цієї рівнодіючої відносно будь-якого полюса
дорівнює головному моменту систему сил відносно цього полюса.
Доказ. Приймемо позначення попереднього доказу. З властивості 3 параграфа 15 одержуємо Мо(S) = Мо(S1), але оскільки система S1 складається з однієї сили F, те Мо(S1) = mo(F).
Таким чином, Мо(S) = mo(F).
§17. Приклади побудови рівнодіючої
1.Дві паралельні сили, спрямовані в одну сторону.
Нехай задані дві паралельні сили F1 і F2, прикладені в точках А и В і спрямовані в одну сторону (мал.18). Використовуємо першу елементарну операцію: додамо дві прямопротилежні сили Р1 і Р2, також прикладені в цих точках. Потім використовуємо третю
|
елементарну |
|
|
операцію: |
||
|
замінимо сили F1 і Р1, |
|||||
|
прикладені в точці А, однією |
|||||
|
силою Q1 = F1 + Р1, також |
|||||
|
прикладеної |
|
в |
точці |
А. |
|
|
Аналогічно сили F2 і Р2, |
|||||
|
прикладені |
|
в |
точці |
В, |
|
|
заміняємо однією силою Q2 = |
|||||
|
= F2 + Р2, також прикладеної в |
|||||
|
точці |
В. |
У |
|
результаті |
|
Мал.18 |
система паралельних сил F1 і |
|||||
F2 перетворюється в систему |
||||||
|
двох |
непаралельних сил Q1 і |
||||
Q2, які лежать в одній площині. Їхні лінії дії перетинаються в точці О. Перенесемо сили Q1 і Q2 уздовж їхніх ліній дії в точку О (це можна зробити за допомогою елементарних операцій), потім знову застосуємо третю елементарну операцію: замінимо сили Q1 і Q2, прикладені в точці О силою F, що і є рівнодіючою сил F1 і F2. Її можна (тобто використовуючи елементарні операції) перенести в точку С перетинання її
19

лінії дії з відрізком АВ. Її положення на відрізку АВ визначається відношенням довжин відрізків АС і СВ. З подоби трикутників AED і
ОАС маємо |
|
P1 |
= |
|
F1 |
. Аналогічно з подоби трикутників BMN і OCB |
|
|
AC |
OC |
|||||
|
|
|
|
|
|||
одержуємо |
|
P2 |
= |
F2 |
|
. Розділимо другу пропорцію на першу. У |
|
|
CB |
|
|||||
|
|
|
|
OC |
|
||
результаті будемо мати (тому що Р1 = Р2)
AC = F2
CB F1
Помітимо, що оскільки F = R = F1 + F2, те рівнодіюча F повинна бути паралельна цим силам і модуль її може бути знайдений з формули
F = F1 + F2 |
(15) |
Резюмуючи вищесказане, можемо сформулювати наступне:
рівнодіюча двох паралельних сил, спрямованих в одну сторону, паралельна силам, спрямована в ту ж сторону і за величиною дорівнює сумі величин сил. Точка прикладення рівнодіючої на відрізку, що з'єднує точки прикладення сил, поділяє цей відрізок у відношенні, зворотному відношенню величин цих сил.
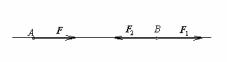
2. Дві нерівні за величиною паралельні сили, спрямовані в
протилежні сторони. |
|
Повторюючи побудови попереднього пункту, |
одержуємо в цьому |
випадку, що лінія дії рівнодіючої проходить за |
межами відрізка АВ. |
Точка З перетинання її з продовженням відрізка АВ визначається пропорцією
|
|
AC |
= |
F2 |
. |
(16) |
|
|
|
|
|||
|
|
BC |
F1 |
|
||
|
Крім того, тому що F= |
|||||
|
= R = F1 + F2, то в да- |
|||||
|
ному випадку |
|
||||
|
|
F = F2 −F1. |
||||
|
Отже, |
|
|
|
||
|
рівнодіюча |
двох |
||||
|
нерівних |
за |
величи- |
|||
|
ною паралельних |
|||||
Мал.19 |
сил, спрямованих у |
|||||
протилежні сторо-
20
