Курс теоретичної механіки 2007 (Укр)

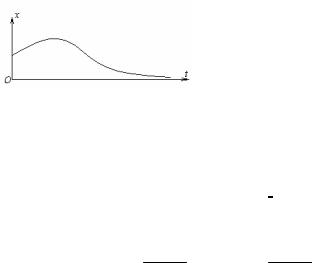
2.Граничний випадок β = k.

Уцьому випадку корені характеристичного рівняння (49) дійсні і рівні один одному:

носить коливального характеру, тобто він є аперіодичним.

Легко перевірити, що він є таким і при інших значеннях хо і Vo .

3.Випадок великого опору β > k.

Уцьому випадку обидва корені є дійсними і негативними

λ1 = − β + β2 − k 2 , λ2 = − β − β2 − k 2 .

Загальне рішення диференціального рівняння (49) представляється в наступному виді:

х = C1 exp (λ1 t) + C2 exp (λ2 t).

Визначивши значення постійних інтегрування з початкових умов (55), одержуємо рівняння руху точки

Графік цієї функції має вид, представлений на мал.11, тобто і

у цьому випадку рух є аперіодичним.

121

− p2 A sin pt +k2 A sin pt = Po sin pt.

Це рівність повинна виконуватися при будь-якім значенні t, тому A (k2 − p2) = Po , тобто

Таким чином, частинне рішення виглядає так

Загальне рішення однорідного рівняння було знайдено в §5

Величини а і α визначаються з початкових умов (55).

Формула (63) показує, що коливання точки під дією збурючої

сили у нерезонансному випадку складаються з власних коливань, що відбуваються з частотою вільних коливань, і вимушених коливань,

що відбуваються з частотою збурючої сили.

Графік залежності амплітуди вимушених коливань

від частоти сили, що вимушує, представлений на мал.12.

Помітимо, що при р = 0 амплітуда | A | = Ро / k2 = Qo / c = δст . Зі збільшенням р при р < k , амплітуда вимушених коливань зростає і

при наближенні р к k вона прагне до нескінченності, потім при р > k зі зростанням р вона прагне до нуля.

Помітимо також, що при р < k знаки А и Ро збігаються, тобто фази вимушених коливань і збурючої сили збігаються, а при р > > k знак А протилежний знаку Ро , тобто фази вимушених коливань і збурючої сили, протилежні. Це значить, що коли збурюча сила спрямована вправо, точка

123

зміщається вліво, і навпаки. Мал.12

2. Резонанс р = k (частота збурючої сили дорівнює частоті

вільних коливань).

У цьому випадку частинне рішення х2 рівняння (59) шукається в наступному виді

Підставивши його в (59), будемо мати

тобто рівняння вимушених коливань виглядає так

x2 = − Po t сos pt.

2p

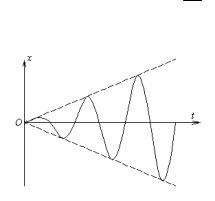
Це означає, що при резонансі зі зростанням t ам-

плітуда коливань росте необмежено по лінійному закону , тобто спостерігається «роз-

гойдування» коливань (мал. 13). У цьому і полягає явище резонансу. Тому воно вважається небезпечним і в багатьох галузях техніки його намагаються уникнути.

Мал.13

§9. Вимушені коливання матеріальної точки при наявності опору

Нехай тепер матеріальна точка рухається під дією трьох сил: відновлючої сили F, обумовленою формулою (31), сили опору R (46) і збурючої сили Q (57). Диференціальне рівняння руху точки в цьому випадку

124

Розділивши обидві частини (66) на m і з огляду на прийняті в попередніх параграфах позначення, одержимо

Це диференціальне рівняння вимушених коливань при наявності

опору.

Загальне рішення його х (як і в попередньому параграфі) представляється у виді

х = х1 + х2 ,

де х1 − загальне рішення однорідного рівняння (тобто рівняння (67) із правою частиною, рівної нулю), а х2 − яке або частинне рішення рівняння (67). Помітимо, що х1 визначає так звані власні коливання, х2

– вимушені коливання.

Вид рішення х1 при різних співвідношеннях параметрів β і k приведений у §7, причому там було показано, що власні коливання, обумовлені цим рішенням, є затухаючими і після деякий проміжок часу практично зникають, тобто загальне рішення для досить великих значень t збігається з х2.

Частинне рішення х2 будемо шукати в наступному виді:

де А и γ − постійні параметри, що підлягають визначенню. Підставляючи (68) у рівняння (67), одержимо

Для того щоб рівність (69) виконувалося при будь-яких значеннях t необхідно, щоб коефіцієнти при sin (pt − γ) і cos (pt − γ) у лівій і правій частинах рівності були рівні:

A (k2 − p2) = Po cos γ, 2βpA = Po sin γ. (70)

Зводячи рівності (70) у квадрат і складаючи їх, одержуємо

125

Рівності (71) і (72) визначають амплітуду і фазу вимушених коли- вань. Графік залежності амплітуди від частоти сили, приведений на мал.14. Як випливає з залежності (71), а також із графіка на мал.14, амплітуда А при будь-якім значенні р, навіть при p = k, приймає кінцеве значення.

§10. Динаміка відносного руху матеріальної точки

Розглянемо рух матеріальної точки М відносно деякої системи відліку xyz, що виконує довільний рух відносно інерціальної системи відліку xoyozo (мал.15). Очевидно, система відліку xyz узагалі

говорячи не є інерціальною.

Рух точки відносно інерціальної системи відліку xoyozo будемо вважати абсолютним, рух її відносно системи відліку xyz будемо вважати відносним, а рух системи xyz відносно xoyozo − переносним.

Складемо основне рівняння динаміки точки для її руху відносно інерціальної системи xoyozo

де через а позначене прискорення точки відносно системи відліку xyz. Підставивши це в основне рівняння динаміки, будемо мати

126

n

ma = ∑Fk − mae − mak .

k=1

Уведемо наступні визначення.

Переносної силою інерції називається вектор, обумовлений за формулою

Je = −mae .

Коріолісовою силою інерції називається вектор, обумовлений за формулою

Jk = −mak .

З урахуванням цих визначень одержуємо

k=1

Рівність (73) зветься основним рівнянням динаміки для відносного руху точки. Таким чином, при складанні основного рівняння

динаміки відносного руху точки необхідно до діючих на точку сил

додати переносну і коріолісову сили інерції.

Розглянемо окремі випадки.

1) Переносний рух поступальний. У цьому випадку Jk , так як і ak дорівнює нулю, і основне рівняння приймає наступний вид:

n

ma = ∑Fk + Je .

k=1

2)Переносний рух поступальний, рівномірний і прямолінійний. У

цьому випадку Jе = Jk = 0 і основне рівняння динаміки приймає такий же вид, як і при русі точки відносно інерціальної системи відліку

n

ma = ∑Fk .

k=1

Це означає, що система відліку, що рухається відносно

інерціальної поступально, рівномірно і прямолінійно сама є інерціальною.

3)Точка нерухома в рухливій системі координат (знаходить-ся в стані відносного спокою). У цьому випадку відносне прискорення а = 0, а також Jk = 0, оскільки Vr = 0. Основне рівняння приймає вид

127

n

∑Fk + Je = 0 .

k=1

Таким чином, при визначенні положення відносного спокою

необхідно до всім діючих на точку силам додати переносну силу інерції.

Приклад. Рух матеріальної точки уздовж поверхні Землі.

Як приклад вивчення відносного руху точки розглянемо її рух по поверхні Землі (мал.16). Нехай точка рухається в північній півкулі в меридіональному напрямку з півдня на північ. Легко переконатися, використовуючи правило Жуковського побудови Коріолісова прискорення, що Коріолісова сила інерції буде мати напрямок, зазначений на кресленні, тобто вправо відносно напрямку руху точки.

При русі в інших напрямках у північній півкулі коріолісова сила інерції має складову, спрямовану в такий спосіб. Це означає, що при русі точки по зем-

.

128