
Курс теоретичної механіки 2007 (Укр)
.pdf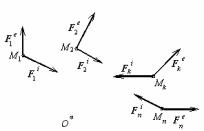
системи відносно цієї осі:
n |
|
Lz = ∑lzk |
(103) |
k=1 |
|
(lzk = mz(qk) − кінетичний момент точки Мk |
механічної системи |
відносно осі z). |
|
Користаючись співвідношенням (99), легко довести наступне твердження:
кінетичний момент механічної системи відносно осі, що проходить через полюс, дорівнює проекції на цю вісь кінетичного моменту механічної системи відносно полюса, тобто
Lz = прz L o |
(104) |
Теорема (про зміну кінетичного моменту механічної системи відносно полюса). Геометрична похідна кінетичного моменту
механічної системи відносно полюса за часом дорівнює головному моменту зовнішніх сил, прикладених до системи, відносно цього полюса:
dLo |
= M e . |
(105) |
|
||
dt |
o |
|
|
|
Доказ. Для кожної з точок механічної системи може бути записана теорема про зміну кінетичного моменту відносно полюса (мал.25)
dlok |
= m |
|
(F e ) + m |
|
(F i ) (k = 1,2,..., n) . |
(106) |
|
o |
o |
||||
dt |
k |
k |
|
|||
|
|
|
|
|
||
Підсумовуючи рівності (106) по k, одержуємо
n |
dlok |
= |
n |
m (F e ) + |
|
|
∑ |
||
∑ dt |
o k |
|||
|
|
|
|
|
k=1 |
|
|
k=1 |
|
n
+ ∑mo (Fki ). k=1
Змінюючи місцями диференцу - Мал.25 вання і підсумовування і врахо - вуючи, що головний момент
внутрішніх сил відносно будь-якого полюса дорівнює нулю, одержуємо (105).
Теорема доведена.
141

Наслідки.
1)Внутрішні сили не впливають на зміну кінетичного моменту механічної системи відносно полюса.
2)(закон збереження кінетичного моменту) Якщо головний момент зовнішніх сил відносно полюса дорівнює нулю протягом деякого проміжку часу, те кінетичний момент механічної системи відносно цього полюса не змінюється ні по величині, ні по напрямку протягом зазначеного проміжку.
Доказ. Якщо M oe = 0, то з теореми випливає, що dLo = 0 , а dt
виходить, Lo = const.
3) (теорема про зміну кінетичного моменту механічної системи відносно осі). Похідна кінетичного моменту механічної системи відносно осі за часом дорівнює сумі моментів зовнішніх сил, прикладених до системи, відносно цієї осі:
n
dLz = ∑mz (Fke ) . (107) dt r=1
Доказ. Запишемо рівність (105) у наступному виді:
dLo |
|
n |
|
|
= |
∑ |
mo (Fke ) |
||
|
||||
dt |
|
|||
|
|
k=1 |
|
|
і спроектуємо його на вісь z. Користаючись формулою (104), а також залежністю між моментами сили відносно полюса й осі, одержуємо (107).
§8. Кінетичний момент твердого тіла, що обертається навколо нерухомої осі
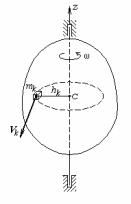
Розглянемо тверде тіло, що обертається навколо нерухомої осі (мал.26). Уявно розіб'ємо тіло на елементарні обсяги (елементарні маси). Одна з таких елементарних мас показана на малюнку. Кількість руху такої елементарної маси дорівнює
qk = mk Vk ,
а кінетичний момент відносно осі z:
lzk = qk hk = mk Vk hk . |
(108) |
142
Швидкість точки обертового тіла визначається за формулою
Vk = ωhk .
Підставивши це в (108), будемо мати
lzk = mk ω hk2 . |
(109) |
Підсумовуючи (109) по всім елементарним масам, утворюючих тіло, одержимо формулу для кінетичного моменту твердого тіла, що обертається навколо нерухомої осі, відносно осі обертання
|
n |
|
|
Lz = ω∑mk hk2 . |
(110) |
|
k=1 |
|
Мал.26 |
Уведемо позначення |
|
|
n |
|
|
J z = ∑mk hk2 |
(111) |
k=1
іназвемо Jz моментом інерції тіла відносно осі z. Таким чином,
моментом інерції тіла відносно осі називається сума добутків елементарних мас, що утворять тіло, на квадрат їхніх відстаней
від осі.
Тоді (110) запишеться так
Lz = Jz ω, |
(112) |
тобто кінетичний момент тіла, що обертається навколо нерухомої
осі, відносно осі обертання дорівнює добутку моменту інерції тіла відносно цієї осі на кутову швидкість обертання.
§9. Моменти інерції деяких тіл
1.Порожній циліндр.
Будемо називати порожнім циліндр, маса якого розподілена по
його поверхні.
Оскільки маса циліндра розподілена по його поверхні, те елементарні маси розташовані також на його поверхні (мал.27) і відстань їх від осі однаково і дорівнює радіусу циліндра R. Тоді
143

n |
|
J z = ∑mk R2 = MR2 . |
(113) |
k=1
(М − маса циліндра).
Мал.27
2.Суцільний однорідний циліндр.
Виділимо із суцільного циліндра порожній циліндр радіуса r < R , товщина стінок якого нескінченно мала і дорівнює dr (мал.28). Його
момент інерції dJz може бути обчислений за формулою (113) dJz = d r2.
Тут d − маса порожнього циліндра. Її неважко визначити в такий спосіб: знаходимо спочатку густина циліндра
|
|
|
ρ = |
|
M |
|
|
|
|
|
|
|
|
πR2H |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
(М − маса суцільного циліндра, R − його |
||||||||||
|
радіус, Н − висота). Потім знаходимо обсяг |
||||||||||
|
порожнього циліндра |
|
|
|
|
||||||
|
|
dV = 2πrdrH. |
|
|
|
|
|||||
|
Тоді |
|
|
|
|
|
|
|
|
|
|
|
d = ρd = |
|
2Mrdr |
, dJz = |
2Mr3dr |
||||||
|
|
|
|
|
|
|
|
. |
|||
|
|
R |
2 |
|
R |
2 |
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
Мал.28 |
Будемо вважати, що суцільний |
циліндр |
|||||||||
|
складається з нескінченної безлічі вкладе- |
||||||||||
них друг у друга порожніх циліндрів, радіуси яких міняються від 0 до R . Тоді
144
R |
|
|
|
R |
|
|
3 |
|
|
J z = ∫dJ z |
= ∫ |
2Mr |
dr . |
||||||
2 |
|
||||||||
0 |
|
|
0 |
|
R |
|
|
||
|
|
|
|
|
|
|
|||
Після інтегрування одержуємо |
|
|
|
|
|
|
|
|
|
J |
|
= |
MR2 |
. |
|
(114) |
|||
z |
|
|
|||||||
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|||
3.Стержень.
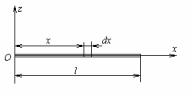
Визначимо момент інерції прямолінійного однорідного стержня відносно осі, яка перпендикулярна стержню і проходить через один з його кінців (мал.29).
Виділимо елемент стержня довжиною dx, що знаходиться на відстані х від осі z. Його маса дорівнює:
Мал.29 |
|
|
|
|
|
|
|
|
|
|
dM = |
M |
dx |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
(М − маса стержня, l − його довжина). Тоді |
|
|
|
||||||||||
J |
|
= |
∑ |
x2dM = l |
Mx2 |
dx . |
|||||||
z |
|
||||||||||||
|
|
|
|
|
∫ |
l |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Після інтегрування одержуємо |
|
|
|
|
|
|
|
|
|||||
|
|
|
J |
|
= |
M l 2 |
. |
|
(115) |
||||
|
|
|
z |
|
|
||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
§10. Моменти інерції відносно паралельних осей (теорема Гюйгенса – Штейнера)
Теорема. Момент інерції Jz тіла відносно деякої осі z дорівнює моменту інерції тіла Jz’ відносно z’, що проходить через центр мас
тіла паралельно даної осі, складеному з добутком маси тіла на квадрат відстані між осями:
Jz = Jz’ + Мd2. |
(116) |
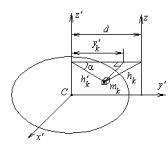
Доказ. Виділимо елементарну масу mk тіла (мал.30). Позначимо через hk відстань від елементарної маси до осі z, а через hk/ - відстань від неї до осі z’. Використовуючи теорему косинусів, можна записати
145
n
Але ∑mk
k=1
(hk)2 = (hk/ )2 + d 2 − 2d hk/ cos α . Але hk/ cos α = yk/ , де yk/ - ордината
маси mk , тобто
(hk)2 = (hk/ )2 + d 2 − 2d yk/ . (117)
Помножимо (117) на mk і просумуємо по всім елементарним масам, що утворять тіло. У результаті одержимо
|
n |
n |
Мал.30 |
J z = J z' + d 2 ∑mk |
− 2d∑mk yk/ . |
|
k=1 |
k=1 |
|
n |
|
дорівнює масі тіла М, а ∑mk yk/ = M yC/ |
= 0 за формулою |
|
k=1
(75) для ординати центра мас, причому вісь у' проходить через центр мас С. Таким чином, маємо
Jz = Jz’ + Мd2,
що збігається з (116).
§11. Приклад рішення задачі з застосуванням теореми про зміну кінетичного моменту механічної системи
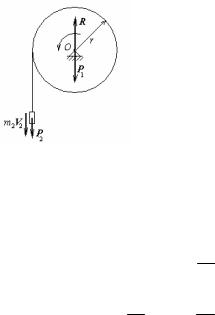
Задача. На однорідний барабан масою m1 = 10 кг і радіусом r = 0,5 м (мал.31) намотана мотузка з вантажем масою m2 = 5 кг на кінці. Зневажаючи масою мотузки і тертям на осі барабана, визначити кутове прискорення барабана.
Рішення. Вісь z обертання барабана перпендикулярна площини креслення і проходить через центр барабана О. Застосуємо теорему про зміну кінетичного моменту механічної системи відносно осі z, вважаючи, що механічна система складається з барабана і вантажу, зовнішніми силами відносно якої є вага барабана Р1 , вага вантажу Р2 і реакція осі барабана R :
dLz |
= P r . |
(118) |
|
||
dt |
2 |
|
|
|
146
кінетичний момент системи складається з кінетичного моменту барабана, обумовленого формулою
L(z1) = J z ω,
і кінетичного моменту вантажу
lz(2) = m2V2 r .
Момент інерції барабана як однорідного циліндра визначається в такий спосіб:
|
|
m r |
2 |
|
|
J z = |
1 |
|
, |
|
2 |
|
||
|
|
|
|
|
Мал.31 |
а швидкість вантажу можна виразити через |
|||
|
кутову швидкість барабана |
|||
V2 = ω r.
Тоді
Lz = L(z1) + lz(2) = (m21 + m2 ) r 2ω.
Підставивши це в (118), будемо мати
(m1 + m2 )r 2 dω = m2 gr , 2 dt
відкіля знаходимо
ε = |
|
m2 g |
= 9,8 с−2 . |
|
|
( |
m1 |
+ m2 )r |
|
||
|
|
|
|||
|
|
|
|
||
|
2 |
|
|
|
|
|
|
§12. Робота сили |
|
||
Нагадаємо, що елементарним переміщенням |
точки (див. §5 глави I |
||||
частини II) називається нескінченно малий вектор |
|||||
|
|
|
dr = Vdt, |
(119) |
|
спрямований по дотичній до траєкторії точки. З (119) випливає, що
|dr| = V dt = ds,
147
тобто довжина елементарного переміщення |
точки дорівнює |
нескінченно малому відрізку дуги траєкторії. |
|
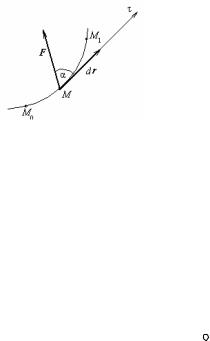
Елементарною роботою сили F (тобто роботою сили на елементарному переміщенні dr) називається скалярна величина
d = F ds cos α , |
(120) |
де α − кут між напрямком сили і дотичної до траєкторії (мал.32). Помітимо, що (120) може бути записане і так
|
d = Fτ ds , |
|
|
|
(121) |
|
тому що проекція |
сили F на напрямок |
дотичної |
дорівнює |
|
||
Fτ = F cos α. Крім того, з (119) випливає |
|
|
|
|
|
|
|
d = F |dr| cos α = (F, dr), |
|
|
(122) |
|
|
|
тобто елементарна робота сили дорівнює |
|||||
|
скалярному |
добутку |
сили |
на |
||
|
елементарне переміщення |
точки. |
|
|||
|
Користаючись |
залежністю |
між |
|||
|
проекціями радіуса-вектора |
точки на осі |
|
|||
|
координат і її координат |
|
|
|
||
Мал.32 |
x = rx , |
y = ry , z = rz , |
|
|
||
рівність (122) можна записати так |
|
|
|
|
|
|
dA = Fx drx + Fy dry + Fz drz = Fx dx + Fy dy + Fz dz. |
(123) |
|
||||
Для того щоб знайти роботу сили на кінцевому переміщенні М0М1 (мал.32) необхідно, просумувати роботи сили на елементарних переміщеннях, тобто
роботою сили на кінцевому переміщенні називається узятий уздовж цього переміщення криволінійний інтеграл від елементарної роботи:
A = ∫dA . |
(124) |
M0M1 |
|
148
§13. Приклади обчислення роботи
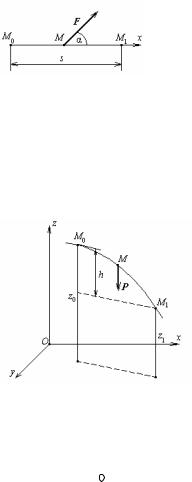
1.Робота постійної сили на прямолінійному переміщенні.
Якщо точка переміщається по прямої (мал.33) і сила, що діє на неї постійна за величиною і напрямком, то криволінійний інтеграл (124) перетворюється в звичайний інтеграл
|
s |
|
Мал.33 |
A = ∫F cosαdx = F scosα , |
(125) |
|
0 |
|
і в результаті одержуємо відому найпростішу формулу обчислення роботи.
2.Робота сили ваги.
Нехай точка М переміщається з положення М0 |
у положення М1 |
|||
|
(мал.34). |
Обрана |
система |
|
|
координат |
показана |
на кресленні |
|
|
(вісь z спрямована |
вертикально |
||
|
нагору). Проекції сили ваги Р на |
|||
|
осі координат рівні |
|
||
|
Рх = Ру = 0, Рz =−Р. |
|||
|
Знайдемо |
елементарну роботу |
||
|
користаючись формулою (123): |
|||
|
|
d = −Pdz. |
||
Мал.34 |
|
|
|
|
|
Тоді робота сили ваги на |
|||
переміщенні М0М1 буде визначатися так |
|
|
|
|
|
z1 |
|
|
|
A = ∫ |
(−P)dz = −P∫dz = P(z0 − z1 ) = Ph . |
(126) |
||
M0M1 |
z0 |
|
|
|
Робота сили ваги не залежить від траєкторії |
точки, а тільки |
|||
від початкового і кінцевого її положень. Вона дорівнює добутку величини сили на падіння висоти положення точки.
149
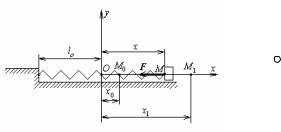
3.Робота пружної сили.
Розглянемо рух вантажу, прикріпленого до пружини, уздовж гладкої горизонтальної площини (мал.35). З боку пружини на вантаж діє сила F, пропорційна подовженню чи укороченню пружини. Виберемо початок координат наприкінці недеформованої пружини. Як показано в §5 глави I проекції сили F на осі координат рівні
Fx = −cx, Fy = Fz =0.
Тоді відповідно до формули (123) маємо
d = −cxdx
і
|
|
|
|
|
x1 |
|
A = |
∫ |
|
dA = −c∫xdx = |
(127) |
||
|
|
|
M0M1 |
x0 |
||
= |
c |
|
(x2 |
− x2 ) |
|
|
|
|
|||||
2 |
|
0 |
|
1 |
|
|
Таким чином, робота
Мал.35 пружної сили дорівнює по-
ловині добутку коефіцієнта жорсткості на різницю квадратів початкового і кінцевого подовжень (чи укорочень) пружини.
4. Робота сил, прикладених до обертового твердому тілу.
Нехай деяке тверде тіло обертається навколо нерухомої осі під дією системи сил F1 , F2 , …, Fn (мал.36). Знайдемо елементарну роботу однієї із сил Fk . Проведемо через точку Мk , до якої прикладена сила, осі натурального тригранника (див.§9 глави I частини II) τ, n і b. За формулою (121)
dA ( Fk ) = Fkτ dsk , |
(128) |
де dsk = Vk dt , Vk - швидкість точки Mk |
пркладення сили Fk . |
Швидкість Vk визначається за формулою |
|
Vk = ω hk ,
hk - відстань від точки Mk до осі обертання. Тоді
150
