
Курс теоретичної механіки 2007 (Укр)
.pdf
§ 4. Аналітичні умови рівноваги для окремих випадків системи сил
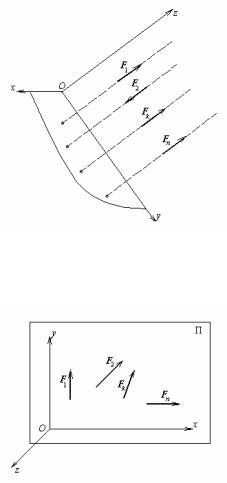
1.Сили, що сходяться. Сили називаються силами, що схо-
дяться, якщо лінії дії сил перетинаються в одній точці, яка має назву точки сходу (мал. 32).
Виберемо початок координат О в точці сходу. Тоді моменти всіх сил відносно полюса О будуть дорівнювати нулю (див. §4 глави I), а отже, буде дорівнювати нулю головний момент системи сил відносно цього полюса. Звідси випливає, що три останніх рівняння (17) задовольняються тотожно, і
рівняннями рівноваги для сил, що сходяться, є наступні
рівняння:
n |
|
1) ∑прx Fk |
= 0, |
k=1 |
|
n |
|
2) ∑прy Fk |
= 0, (20) |
k=1 |
|
n |
|
3) ∑прz Fk |
= 0. |
k=1
Рівності (20) виражають рівність нулю проекцій головного вектора R на осі
Мал.32 координат, а значить і рівність нулю самого головного вектора. Таким чином, для того щоб тіло під дією сил, що
сходяться, знаходилося в рівновазі, необхідно і досить, щоб головний вектор цих сил дорівнював нулю.
2.Паралельні сили.
Розглянемо систему паралельних сил (мал.33). Виберемо систему координат у такий спосіб: вісь z направимо паралельно лініям дії сил, тоді осі x і y виявляться їм перпендикулярними. Тоді проекції всіх сил на осі x і y будуть дорівнювати нулю, тобто перших два рівняння (17) задовольняються тотожно. Крім того, моменти всіх сил відносно осі z також дорівнюватимуть нулю, тому що їхні лінії дії паралельні цієї осі. Тому і шосте рівняння (17) задовольняється тотожно.
31
Таким чином,
рівняннями рівноваги паралельних сил є наступні рівняння:
n |
|
1) ∑прz Fk |
= 0, |
k=1 |
|
n |
|
2) ∑mx Fk |
= 0, (21) |
k=1 |
|
n |
|
3) ∑my Fk |
= 0. |
k=1
Мал.33
3.Плоска система сил.
|
Нехай |
система |
сил |
|
|
розташована |
в площині Π. |
||
|
Проведемо осі x і y у цій |
|||
|
площині, а вісь z – |
|||
|
перпендикулярно |
їй. |
||
|
Очевидно, лінії дії всіх сил |
|||
|
перпендикулярні осі z, тому |
|||
|
проекції всіх сил на вісь z |
|||
|
дорівнюють |
нулю, тобто |
||
|
третє |
рівняння |
(17) |
|
|
задовольняється |
тотожно. |
||
|
Крім того, моменти всіх сил |
|||
|
відносно осей x і y дорівню- |
|||
Мал.34 |
нюють нулю, тому що ці осі |
|||
|
лежать |
в одній площині із |
||
силами, а отже, лінії дії сил або паралельні цим осям, або їх перетинають. Таким чином, четверте і п'яте рівняння (17) також задовольняються тотожно, і рівняннями рівноваги плоскої системи
сил є наступні рівняння:
32

n |
n |
n |
|
|
|
1) ∑прx Fk |
= 0, 2) ∑прy Fk |
= 0, 3) ∑mz Fk = 0, |
|
(22) |
|
k=1 |
k=1 |
k=1 |
|
|
|
Приклад 1. |
Визначення опорних реакцій |
балки, що |
|||
|
|
знаходиться |
під |
||
|
|
дією плоскої сис- |
|||
|
|
теми сил. |
|
||
|
|
На |
мал.35 |
зоб- |
|
|
|
ражена |
вигнута |
||
|
|
балка, |
що знахо- |
||
|
|
диться |
під |
дією |
|
|
|
сил Р1 і Р2 , а |
|||
|
|
також пара сил з |
|||
|
|
моментом М. Усі |
|||
|
Мал.35 |
ці сили лежать у |
|||
|
|
однієї |
площини, |
||
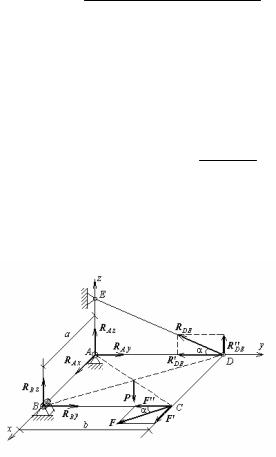
що збігає з площиною креслення. Задано наступні величини: Р1 =10 кН, Р2 =4 кН, М = 5 кНм, α = 30о. Необхідно знайти реакції нерухомого шарніра А и стержня В (вісь шарніра перпендикулярна площини, у якій лежать сили).
Рішення. У параграфі 20 глави I було показано, що реакція нерухомого шарніра RA розкладається на дві складові RAx і RAy у площині, перпендикулярній осі шарніра, тобто в площині креслення. Реакція стержня RВ спрямована уздовж осі стержня, тобто в даному випадку вертикально. У результаті додавання цих сил до заданих, одержуємо систему сил, показану на мал. 34. Балка знаходиться в рівновазі під дією цієї системи сил. Тому виконуються рівняння рівноваги для плоскої системи сил. Для того, щоб спростити їхнє
складання, розкладемо силу Р2 на дві складові: P |
/ |
= Р2 sin α |
і P// |
= Р2 |
|
|
2 |
|
2 |
|
|
cos α. Складемо рівняння: |
|
|
|
|
|
n |
|
|
|
|
|
∑прx Fk |
=RAx + P2 sin α = 0 |
|
|
|
|
k=1 |
|
|
|
|
|
n |
|
|
|
|
|
∑прy Fk |
= RAy − P1 + RB − P2 cos α = 0 |
|
|
|
|
k=1
n
∑mz (Fk ) = M − 4P1 + 5RB −8P2 cos α − 2P2 sin α = 0
k=1
33
При складанні останнього рівняння було враховано, що вісь z перпендикулярна площини креслення, тобто всі сили лежать у площині, перпендикулярної цієї осі, і при обчисленні моментів відносно цієї осі можна використовувати спрощене правило (див. властивість 3 з §3 глави I).
З останнього рівняння знаходимо
RB = −M + 4P1 + 8P25cos α + 2P2 sin α = 13,34 кН.
З першого рівняння одержуємо
RAx = - P2 sin α =- 2 кН,.
А з другого
RAy = P1 – RB + P2 cos α = 0,12 кН.
Тому що RA = RAx +RAy , те RA = 
 RAx2 + RAy2 = 2,004 кН.
RAx2 + RAy2 = 2,004 кН.
Приклад 2. Визначення опорних реакцій плити, що знаходиться під дією просторової системи сил.
Однорідна прямокутна плита ABCD вагою Р = 10 кН спирається
|
на нерухомий сфе- |
|
ричний шарнір у |
|
точці А (мал.36). У |
|
точці В неї підтри- |
|
мує нерухомий ци- |
|
ліндричний шарнір, |
|
вісь якого збігається |
|
з віссю х, а в точці D |
|
– стержень DE. У |
|
точці С на неї діє |
|
сила F = 20 кН у |
|
площині плити під |
|
кутом α до ребра ВР. |
|
Необхідно знайти |
Мал.36 |
реакції опор плити, |
|
якщо α = 30о і |
b/a = 2. |
|
34
Рішення. У §20 глави I було показано, що реакція сферичного шарніра RA має три складові RAx , RAу , RAz уздовж трьох осей координат х,у и z, а реакція RВ – дві складові RВу і RВz у площині, перпендикулярній осі шарніра, тобто осі х. Реакція RDE стержня DE повинна бути спрямована уздовж осі стержня. Розкладемо реакцію
стержня RDE на дві складові RDE/ = RDE cosα і RDE// = =RDE sinα, паралельні осям y і z. Аналогічно розкладається сила F: на силу F/ = F sinα, паралельну осі х, і силу F// = F cosα, паралельну осі в. Таким чином, плита знаходиться в рівновазі під дією просторової системи сил, показаної на мал. 36. Складаємо рівняння рівноваги:
n |
|
|
|
|
|
∑прx Fk |
=RAx + F sin α = 0, |
||||
k=1 |
|
|
|
|
|
n |
|
|
|
|
|
∑прy Fk = RAy + RBy − RDE cos α − F cos α = 0, |
|||||
k=1 |
|
|
|
|
|
n |
|
|
|
|
|
∑прz Fk |
=RAz + RBz + RDE sin α − P = 0, |
||||
k=1 |
|
|
|
|
|
n |
|
|
|
|
|
∑mx |
(Fk ) = bRDE sin α − |
b |
P = 0, |
||
|
|||||
k=1 |
2 |
|
|||
|
|
|
|
|
|
n |
|
|
|
|
|
∑my |
(Fk ) = − aRBz + |
a |
P = 0, |
||
|
|||||
k=1 |
2 |
|
|
|
|
|
|
|
|
|
|
n
∑mz (Fk ) = aRBy − aF cos α − bF sin α = 0.
k=1
Зпершого рівняння знаходимо
RAx = - F sinα = -10 кН.
З четвертого рівняння:
RDE = Р = 10 кН.
З п'ятого рівняння:
RBz = Р/ 2 = 5 кН.
35

Із шостого рівняння:
RВу = F cosα + b F sin α = 37,3 кН. a
Підставивши знайдені значення реакцій у друге і третє рівняння, знаходимо
RAy = - RBy +RDE cosα +F cosα = 8,67 кН, RAz = - RBz - RDE sinα +P = 0.
Тому що RA = RAx + RAy + RAz , то
RA = 
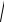 RAx2 + RAy2 + RAz2 = 13,23 кН.
RAx2 + RAy2 + RAz2 = 13,23 кН.
Тому що RВ = RВy + RВz , то
RB = 
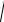 RBy2 + RBz2 = 37,63 кН.
RBy2 + RBz2 = 37,63 кН.
36
Г Л А В А III
ПРИВЕДЕННЯ СИСТЕМИ СИЛ ДО НАЙПРОСТІШОГО ВИДУ
§ 1. Загальна ознака еквівалентності систем сил
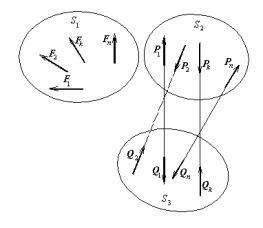
Теорема. Для того щоб дві системи сил S1{F1,F2,…,Fn}і S2{Р1,Р2,…,Рm} були еквівалентними, необхідно і досить, щоб їхні
головні вектори і головні моменти відносно того самого полюса
були геометрично рівні.
Необхідність умов еквівалентності (тобто те, що з еквівалентності двох систем сил випливає рівність їхніх головних векторів і головних моментів відносно того самого полюса ) випливає безпосередньо з властивості 3 еквівалентних систем сил (§15 глави I).
Доведемо достатність умов еквівалентності (тобто що з рівностей
R(S1) = R(S2), Mo(S1) = Mo(S2) |
(23) |
випливає S1 ~ S2 ).
Уведемо додаткову систему сил
S3{Q1,Q2,…,Qm},сили якої прямопротилежні
силам системи
S2{Р1,Р2,…,Рm} і розглянемо систему S, що
складається із сил, що входять в усі три системи S1 , S2 і S3, тобто
S = S1 U S2 U S3 . (24)
Оскільки системи S2 і S3 складаються із взаємно прямопролеж-
Мал.37 них сил, то використовуючи m разів дру-
гу елементарну операцію, їх можна видалити. У результаті від системи S залишиться тільки система сил S1, тобто ця система була отримана із системи S за допомогою елементарних операцій. Це значить, що
37
S1 ~ S. |
(25) |
Розглянемо тепер систему S4, що складається із сил, що входять у системи S1 і S3, тобто
S4 = S1 U S3 . |
(26) |
Помітимо, що при цьому з (24) випливає, що
S = S2 U S4 . |
(27) |
Знайдемо головний вектор системи S4:
R(S4) = R(S1) + R(S3), |
(28) |
Тому що {Pk,Qk} – п.п.с., тобто Pk = − Qk (k = 1,2,…,n), то R(S3) =
=−R(S2). Але за умовою R(S2) = R(S1) . Таким чином, R(S3) = − R(S1), і з (28) одержуємо
R(S4) = 0.
Зовсім аналогічно доводиться, що
Mo(S4) = 0.
Використовуємо тепер основну лему статики і за допомогою елементарних операцій приведемо систему S4 до двох сил P і Q. З властивості 3 еквівалентних систем сил (§15 глави I) випливає, що
P + Q = R(S4) = 0,
mo(P) +mo(Q) = Mo(S4) = 0.
Такими властивостями володіють тільки дві прямопротилежні сили, тобто {P,Q} – п.п.с. Використовуємо тепер другу елементарну операцію і видалимо ці сили. Нагадаємо, вони були отримані з S4 за допомогою елементарних операцій. Таким чином, система S4 зникає і від системи S (див.(26)) залишається только система S2. Це значить, що
S ~ S2 .
Зіставляючи це співвідношення з (25) і використовуючи властивість 2 еквівалентних систем сил (§15 глави I), одержуємо
38
S1 ~ S2
(що і було потрібно довести).
Наслідок 1 (ознака еквівалентності пар). Для того щоб дві пари сил були еквівалентними, необхідно і досить, щоб їхні моменти
були геометрично рівні.
Доказ. Головний вектор пара сил дорівнює нулю, у такий спосіб умова геометричної рівності головних векторів будь-яких пар сил виконано. Звідси випливає, що необхідною і достатньою умовою еквівалентності пар сил є геометрична рівність їхніх моментів.
Наслідок 2 (теорема про додавання пар). Система пар сил еквівалентна а) парі сил, момент якої дорівнює геометричній сумі моментів
пар, що входять у систему, у тому випадку, коли ця геометрична сума відмінна від нуля; б) двом прямопротилежним силам, якщо геометрична сума
моментів пар дорівнює нулю.
Доказ.
Випадок а). Головний вектор системи пар сил S{P1,Q1,P2,Q2,…,Pm,Qm}дорівнює нулю, тому що головний вектор кожної з них дорівнює нулю, тобто Pi+Qi = 0 (i=1,2,…,m)... У такий спосіб головні вектори системи пар й однієї пари сил геометрично рівні завжди. Тому для еквівалентності системи пар сил S{P1,Q1,P2,Q2,…,Pm,Qm}одній парі S1{P,Q}достатнє виконання умови геометричної рівності їхніх головних моментів, тобто рівності геометричної суми моментів пар, що входять у систему S{P1,Q1,P2,Q2,…,Pm,Qm},моменту пари S1{P,Q}, що відмінний від нуля (див. §12 глави I).
Випадок б). Якщо геометрична сума моментів пар, що утворяють систему S{P1,Q1,P2,Q2,…,Pm,Qm},дорівнює нулю, то тим самим виконуються дві умови
R(S)=0, M(S)=0.
Але таким же умовам задовольняють і дві прямопротилежні сили.
§2. Еквівалентні перетворення пар
Знаслідку 1 попереднього параметра випливає, що будь-які пере-
39
творення однієї пари сил в іншу, що залишають її момент незмінним, приводять до пари, еквівалентної вихідної.
Перетворення пари, що не змінюють її моменту, називаються
еквівалентними.
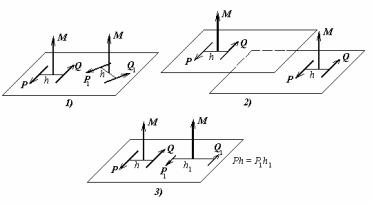
Приведемо деякі приклади еквівалентних перетворень:
1. переміщення пари у своїй площині без зміни величини сил, плеча і напрямку обертання,
2. перенос пари зі своєї площини в паралельну їй площина без зміни величини сил, плеча і напрямку обертання,
3.одночасна зміна величини сил, що утворять пару, і її плеча,
при якому залишається незмінним добуток величини сил на плече.
Неважко переконатися, що у всіх трьох випадках не міняється ні напрямок моменту, ні його величина (мал.38).
Мал.38
§ 3. Теорема Пуансо про приведення системи сил до заданого центра
Будь-яка система сил S еквівалентна системі S1{F,P,Q} із трьох
сил, перша з яких F геометрично дорівнює головному вектору R системи S і прикладена в будь-який заздалегідь обраної точці O
(іменованої центром приведення), а інші дві утворяють а) пару сил з моментом М, рівним головному моменту Мо
системи S відносно центра приведення О, якщо цей головний
момент відмінний від нуля; б) дві прямопротилежні сили, якщо головний момент Мо
системи S відносно центра O приведення дорівнює нулю.
40
