
Курс теоретичної механіки 2007 (Укр)
.pdf
Доказ.
Випадок а). Знайдемо головний вектор системи S1, зображеної на мал.39:
|
R(S1) = F + P + Q = F. |
|
|
Але F = R(S) за умовою. Тоді |
|
|
виявляється, що |
|
|
R(S1) = R(S). |
(29) |
|
Аналогічно, |
|
Мал.39 |
Mo(S1) = mo(F) + mo(P) +mo(Q) |
|
Але mo(F) = 0, тому що сила F прикладена в центрі приведення О, а
mo(P) +mo(Q) =М, |
|
який за умовою дорівнює Мо(S1). Таким чином, |
|
Mo(S1) = Mo(S). |
(30) |
З (29) і (30), а також із загальної ознаки еквівалентності |
систем |
сил одержуємо |
|
S ~ S1. |
|
Випадок б). Очевидно, що й у цьому випадку |
|
R(S1) = F + P + Q = R(S), |
(31) |
а |
|
Mo(S1)=mo(F)+mo(P+mo(Q)=0=Mo(S), |
(32) |
тому що mo(P) +mo(Q) = 0, оскільки {P,Q} – Мал.40 п.п.с. З (31), (32) і загальної ознаки эквіва-
лентності систем сил випливає
S ~ S1.
Теорема Пуансо доведена.
41

§4. Окремі випадки теореми Пуансо
1.R(S) = 0, Mo(S) = 0.
Уцьому випадку F = 0, і система S еквівалентна двом
прямопротилежнним силам S1{P,Q}.
2.R(S) = 0, Mo(S) ≠ 0.
Уцьому випадку також F = 0, але через те, що Mo(S) ≠ 0, система
S еквівалентна парі сил S1{P,Q}.
3.R(S) ≠ 0, Mo(S) = 0.
Уцьому випадку F ≠ 0, але з того, що Mo(S) = 0, випливає {P,Q} –
п.п.с. (мал.39). Використовуючи другу елементарну операцію, видаляємо їх. У результаті одержуємо
S ~ S1{F},
тобто система S приводиться до однієї сили – рівнодіючої.
4.R(S) ≠ 0, Mo(S) ≠ 0, R(S) Mo(S).
|
Тому що площина пари сил перпенди- |
|
|
кулярна її моменту, то в цьому випадку |
|
|
виявляється, що сила F, рівна |
R(S), пара- |
|
лельна площини пари {P,Q}. Шляхом пере- |
|
|
носу пари в паралельну площину (див. §2) |
|
|
можна домогтися того , щоб F, P і Q вия- |
|
|
вилися в одній площині Π. Потім переміща- |
|
|
ючи її в цій площині і змінюючи величини |
|
|
сил і плече так, щоб момент залишився не- |
|
|
змінним, можна домогтися того, щоб одна |
|
Мал.41 |
із сил P пара стала прямопротилежною |
|
|
силі F (мал.41). Використовуючи тепер |
|
другу елементарну операцію, відкинемо дві прямопротилежні сили F і |
||
P. У результаті в системі S1 залишиться тільки одна сила Q, що і буде |
||
рівнодіючої системи сил S. Таким чином, у цьому випадку |
система S |
|
приводиться до однієї сили – рівнодіючої. |
|
|
5. R(S) ≠ 0, Mo(S) ≠ 0, R(S) не перпендикулярний Mo(S). |
||
Розкладемо Mo(S) на дві складові Mo/ і Mo// , причому |
Mo/ R(S) , |
|
а Mo// || R(S) (мал.42а). Ця процедура відповідає уявленню пари з моментом Mo(S) у виді двох пар: одну з моментом Mo/ , а другу - з мо-
42

ментом Mo// . за теоремою про додавання пар ці пари еквівалентні вихідної. Оскільки
Mo/ (S) F (тому що F = R(S)), то пара {P,Q}з таким моментом може бути аналогічно попередньому випадку побудована так, що F і Р виявляться прямопро-
Мал.42 тилежними силами. Після вида-
лення їх із трьох сил F, Р и Q залишиться только сила Q. Однак є ще пара сил {P1,Q1} з моментом Mo// (мал.42б). Оскільки Mo// || Q (тому що Q = F), то пара {P1,Q1} лежить у площині Π1, перпендикулярної Q.
Система трьох сил {Q, P1, Q1}, дві з яких P1, Q1 утворять пару, що лежить у площині, перпендикулярної третьому вектору Q, називається динамой. Таким чином, у цьому випадку система S
приводиться до динами.
§ 5. Найпростіші системи сил
Оскільки окремі випадки 1 – 5 теореми Пуансо вичерпують усі логічно можливі варіанти значень R і Mo , можна зробити висновок про те, які існують типи найпростіших систем сил, до яких може бути приведена система сил S за допомогою елементарних операцій:
1.дві прямопротилежні сили (якщо R(S) = 0, Mo(S) = 0),
2.пара сил( якщо R(S) = 0, Mo(S) ≠ 0),
3.одна сила (рівнодіюча) (якщо R(S) ≠ 0, Mo(S) = 0 або R(S) ≠ 0,
Mo(S) ≠ 0, R(S) Mo(S)),
4. динама (якщо R(S) ≠ 0, Mo(S) ≠ 0, R(S) не перпендикуляр-
ний Mo(S)).
Залишається відкритим питання: чи не може та сама система сил бути приведена до різних найпростіших систем за рахунок вибору центра приведення? Для з'ясування цього питання вводяться спеціальні величини, зв'язані із системами сил, іменовані інваріантами.
Інваріантами систем сил, називаються величини (скалярні чи векторні), що не залежать від центра приведення цих систем
43
до найпростішого виду (тобто є характеристиками самих цих систем).
Таких інваріантів три:
1. перший інваріант I1 (S) = R (тобто головний вектор системи
сил),
2.другий інваріант I2 (S) = (R, Mo) (тобто скалярний добуток головного вектора на головний момент відносно центра приведення О),
3.третій інваріант I3 (S) = Mo, якщо R = 0 (тобто головний момент системи сил, головний вектор якої дорівнює нулю).
Те, що I1 (S) дійсно є інваріантом, очевидно.
Переконаємося, що I2 (S) є інваріантом. Для цього скористаємося формулою 13 параграфа 11 глави I:
|
|
|
|
|
|
Mo' = Mo +[O1O, R] . |
(32) |
||||
Тоді |
|
||||
|
|
|
|
||
(R, Mo ) = (R, Mo ) + (R,[O1O, R]) . |
(33) |
||||
1 |
|
|
|
|
|
Тому що векторний добуток двох векторів являє собою вектор,
|
|
|
|
|
|
|
перпендикулярний |
векторам, що |
перемножується, [O1O, R] R , то |
||||
|
|
|
|
|
||
(R,[O1O, R]) , = 0 |
як скалярний |
добуток двох взаємно перпенди- |
||||
кулярних векторів. З (33) одержуємо (R, Mo1 ) = (R, Mo ) для будь-яких
центрів приведення О1 і О, відкіля і випливає необхідне. Те, що I3 (S) є інваріантом, випливає з формули (32).
Теорема. Еквівалентні системи сил мають рівні інваріанти.
Доказ випливає з того, що еквівалентні системи сил мають геометрично рівні головні вектори і головні моменти відносно того самого полюса.
Наслідок. Якщо система сил приводиться за допомогою елементарних операцій до однієї з найпростіших систем сил, то
вона не може бути приведена до іншої найпростішої системи.
Доказ. Знайдемо значення інваріантів найпростіших систем сил, використовуючи частинні випадки теореми Пуансо і вищедоведену теорему:
1.дві прямопротилежні сили:
I1 = R = 0, I2 = (R, Mo) = 0, I3 = Mo = 0;
2.пара сил:
I1 = R = 0, I2 = (R, Mo) = 0, I3 = Mo ≠ 0;
44
2.одна сила (рівнодіюча):
I1 = R ≠ 0, I2 = (R, Mo) = 0 (тому що або Mo = 0, або R Mo), I3 не існує, тому що R ≠ 0,
3.динама:
I1 = R ≠ 0, I2 = (R, Mo) ≠ 0 (тому що R ≠ 0, Mo ≠ 0 і R не перпендикулярний Mo), I3 не існує, тому що R ≠ 0.
Переглянувши приведені вище значення інваріантів найпростіших систем сил, можна відзначити, що в будь-яких двох з цих систем маються незбіжні значення принаймні одного інваріанта. Звідси випливає, що та сама система сил не може бути приведена до двох різних найпростіших систем, тому що це значило б, що вони еквівалентні один одному, що суперечить теоремі.
Користаючись приведеними вище значеннями інваріантів найпростіших систем сил, легко сформулювати ознаки приведення системи сил до рівнодіючої і до динами.
Ознака приведення системи сил до рівнодіючої. Для того щоб система сил мала рівнодіючу, необхідно і досить, щоб R ≠ 0, (R, Mo) = 0, тобто щоб головний вектор системи був відмінний від
нуля, а скалярний добуток головного вектора на головний момент дорівнювало нулю.
Ознака приведення системи сил до динами. Для того щоб система сил приводилася до динами, необхідно і досить, щоб (R, Mo) ≠ 0, тобто щоб скалярний добуток головного вектора на
головний момент був відмінний від нуля.
Тут враховано, що з нерівності (R, Mo) ≠ 0 випливає, що R ≠ 0.
45
Г Л А В А IV
ЦЕНТР ПАРАЛЛЕЛЛЬНЫХ СИЛ І ЦЕНТР ВАГИ
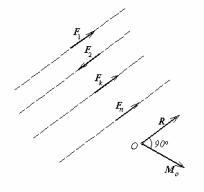
§ 1. Умова існування рівнодіючої паралельних сил
Розглянемо систему |
паралельних сил S{F1,F2,…,Fn}(тобто |
|||
F1||F2||…||Fn)(мал.43). |
Головний |
вектор |
цієї |
системи |
|
|
n |
|
|
|
|
R = ∑Fk паралельний |
лініям |
|
k=1
дії сил, якщо він відмінний від нуля. Момент кожної із сил mo(Fk) (k=1,2,…,n) перпендикулярний лініям дії сил, тому що він перпендикулярний площини, що проходить через лінії дії сили і полюс. Звідси випливає, що головний момент системи сил
|
|
n |
|
Mo |
= ∑mo (Fk ) |
|
|
k=1 |
Мал.43 |
перпендикулярний лініям дії |
|
|
сил. Таким |
чином, R Mo, і |
виходить, (R , Mo) =0. Тоді ознака існування рівнодіючої (§5 попередньої глави) для паралельних сил виглядає так:
Для того щоб система паралельних сил мала рівнодіючу, необхідно і досить, щоб R ≠ 0, тобто щоб її головний вектор не
дорівнював нулю.
§ 2. Центр паралельних сил
Почнемо з приклада. Розглянемо дві паралельні сили F1 і F2, спрямовані в одну сторону (мал.44). Як показано в §17 глави I, положення точки прикладення рівнодіючої на відрізку АВ визначається рівністю
AC |
= |
F2 |
. |
(34) |
|
|
|||
CB F1 |
|
|||
46

Повернемо сили F1 і F2 навколо їхніх точок прикладення А и В на той самий кут α зі збереженням їхньої величини і паралельності. Тоді рівнодіюча також повернеться на кут α, причому точка її прикладення на відрізку АВ залишиться незмінної, тому що співвідношення (34) залишається чинним і для повернених сил.
Мал.44 Виявляється, що подібна точка існує і у більш загальному випадку паралель-
них сил.
Центром паралельних сил називається точка прикладення рівнодіючої цих сил, навколо якої рівнодіюча повертається при повороті всіх сил навколо їхніх точок прикладення на той самий кут зі збереженням паралельності.
Теорема. Якщо система паралельних сил має рівнодіючу, то вона має і центр паралельних сил, радіус-вектор якого визначається за формулою
|
n |
|
|
∑Fk rk |
|
r = |
k=1 |
(35) |
|
||
c |
n |
|
|
∑Fk |
|
k=1
(тут rk – радіус-вектор точки додатка сили Fk, а Fk = ±| Fk |, де знак вибирається відповідно до правила, приведеного у доказі теореми).
Доказ. Розглянемо систему паралельних сил S{F1,F2,…,Fn} (мал.45). Введемо одиничний вектор е, паралельний силам. Тоді кожну силу можна представити в наступному вигляді:
Fk = Fk e (k = 1,2,…,n),(36)
де Fk = ± | Fk |, де знак + вибирається у випадку збігу напрямків векторів Fk і е, і знак – у протилежному випадку.
Нехай система S має рівнодіючу F.
Тоді, |
використовуючи |
представлення, |
можемо записати |
|
|
Мал.45 |
F = F e, |
(37) |
47
n |
|
де F = ∑Fk , тому що |
|
k=1 |
|
n |
n |
F = R = ∑Fk = ∑Fk e . |
|
k=1 |
k=1 |
Відповідно до узагальненої теореми Вариньона (§16 глави I) можна записати наступну рівність
n |
|
mo (F) = ∑mo (Fk ) |
(38) |
k=1
Використовуючи представлення моменту сили відносно полюса у вигляді векторного добутку (§5 глави I), а також (36) і (37), можна представити (38) так:
n |
|
[rc , Fe] = ∑[rk , Fk e] |
(39) |
k=1 |
|
Переносячи праву частину (39) ліворуч і використовуючи властивості векторного добутку, одержуємо
n |
|
[Frc − ∑Fk rk , e] = 0 |
(40) |
k=1
Будемо тепер повертати вектор е. Унаслідок рівностей (36) і (37) це приведе до повороту векторів Fk (k=1,2,…,n) і F зі збереженням їхньої паралельності. Будемо вважати, що вектори Fk (k=1,2,…,n) повертаються навколо їхніх точок прикладення, тобто точки прикладення цих сил, а виходить, і радіуси-вектори rk (k=1,2,…,n) залишаться незмінними. Крім того, тому що ми розшукуємо центр паралельних сил, тобто точку прикладення рівнодіючої, що залишається неіменної при поворотах сил, то і вектор rc теж повинний залишатися незмінним. Таким чином, лівий множник векторного добутку в (40) залишається незмінним, у той час як правий множник може повертатися довільно. Звідси випливає, що збереження рівності (40) при цьому може дотримуватися тільки при
n |
|
Frc − ∑Fk rk = 0 |
(41) |
k=1
Зумови існування рівнодіючої паралельних сил випливає
48

n |
|
F = ∑Fk ≠ 0 |
(42) |
k=1
Зурахуванням цієї нерівності з (41) одержуємо (35). Ця рівність показує, що центр паралельних сил існує, якщо виконана нерівність (42), тобто якщо існує рівнодіюча.
Теорема доведена.
Спроектуємо векторну рівність (35) на осі координат. Зі співвідношень
|
|
x = прx r, |
y = пру r, |
z = прz r |
|
|
|
||||
( r – радіус-вектор точки; x, y, z – її координати) одержуємо |
|
||||||||||
|
|
n |
|
|
|
n |
|
|
n |
|
|
|
|
∑Fk xk |
|
|
|
∑Fk yk |
∑Fk zk |
|
|||
xc |
= |
k=1 |
, |
yc |
= |
k=1 |
|
, zc = |
k=1 |
|
(43) |
n |
n |
|
n |
||||||||
|
|
∑Fk |
|
|
|
∑Fk |
|
|
∑Fk |
|
|
|
|
k=1 |
|
|
|
k=1 |
|
|
k=1 |
|
|
Формули (43) дозволяють знайти координати центра паралельних сил.
§ 3. Центр ваги
Центром ваги тіла називається центр паралельних сил ваги елементарних мас, що утворяють тіло, тобто центр ваги тіла – це така точка прикладення рівнодіючих сил ваги елементарних мас, що залишається незмінною при будь-яких поворотах тіла. Під елементарними масами розуміються маси малих частин
(елементарних обсягів),з яких складається тіло.
На мал.46 зображене деяке тіло. Розіб'ємо його на елементарні обсяги (деякі з них показані на малюнку). Ваги цих елементарних обсягів (елементарних мас) утворяють систему паралельних сил. Очевидно, вони мають рівнодіючу, тому що вони спрямовані в одну сторону, і їхня сума не може дорівнювати нулю. Отже, існує центр цих паралельних сил, тобто центр ваги тіла. Його координати можуть бути знайдені з формул (43) при заміні Fk на Pk :
Мал.46
49
|
|
n |
|
|
|
n |
|
|
|
n |
|
|
|
∑Pk xk |
|
|
|
∑Pk yk |
|
|
|
∑Pk zk |
|
xc |
= |
k=1 |
, |
yc |
= |
k=1 |
, |
zc |
= |
k=1 |
(44) |
n |
n |
n |
|||||||||
|
|
∑Pk |
|
|
|
∑Pk |
|
|
|
∑Pk |
|
|
|
k=1 |
|
|
|
k=1 |
|
|
|
k=1 |
|
§ 4. Статичні моменти
Величини, що стоть у чисельниках формул (44), називаються
статичними моментами, тобто
n |
n |
n |
S yz = ∑Pk xk , Sxz = ∑Pk yk , Sxy = ∑Pk zk . |
||
k=1 |
k=1 |
k=1 |
Тоді (44) можна записати так:
xc = |
S yz |
, yc = |
S |
xz |
, zc = |
Sxy |
. |
P |
|
|
P |
||||
|
|
P |
|
||||
Властивості статичних моментів.
(45)
(46)
1.Якщо тіло складається з декількох тіл, то статичний мо-
мент тіла дорівнює сумі статичних моментів цих тіл.
Доказ випливає з того факту, що розбивка тіла в цьому випадку на елементарні маси можна зробити шляхом розбивки на елементарні маси окремих тіл, що утворяють дане тіло.
2. Якщо відомі координати центра ваги тіла, то його статичні моменти можна визначити з формул
S yz = Pxc , Sxz = Pyc , Sxy = Pzc . |
(47) |
Ці формули випливають з формул (46).
§ 5. Центри ваги симетричних тіл
Теорема. Якщо тіло має площину (або вісь, або центр) матеріальної симетрії, то центр ваги тіла лежить на цій площині (на цій осі, у цьому центрі).
50
