
Курс теоретичної механіки 2007 (Укр)
.pdf
|
|
|
|
|
|
|
h3 = 4R . |
|
|
|
|
||||
Звідси випливає, що робота зовнішніх сил дорівнює: |
|
||||||||||||||
Ae = (P1 + P2 ) 2R + P3 4R = (2m1 +6m2 ) gR. |
(160) |
||||||||||||||
Підставляючи (148), (149), (159) і (160) у (147), одержуємо |
|
||||||||||||||
( |
8m1 |
+11m |
2 |
)ω2 R2 |
= 2(m + 3m |
2 |
)gR , |
|
|||||||
|
|
||||||||||||||
3 |
|
|
|
1 |
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
відкіля знаходимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
ω1 = |
2(m1 + 3m2 )g |
|
|
= 2,47 з−1. |
|
|||||||||
|
|
|
|||||||||||||
|
|
( |
8m1 |
+11m2 )R |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
161
Г Л А В А III
ЕЛЕМЕНТИ АНАЛІТИЧНОЇ МЕХАНІКИ
§1. Зв'язки
Механічна система називається вільної, якщо на переміщення її точок і їхніх швидкостей не накладені ніякі обмеження. У протилежному випадку система називається невільною.
Обмеження, що накладаються на переміщення і швидкості
точок невільної механічної системи, називаються зв'язками.
Математично зв'язки можуть бути виражені за допомогою рівностей чи нерівностей (що буде видно з прикладів, приведених нижче).
Приведемо класифікацію зв'язків.
а) Зв'язки поділяються на утримуючі і неутримуючі. Утримуючими називаються зв'язки, математичне вираження
яких являє собою рівність. У протилежному випадку зв'язки
називаються неутримуючими.
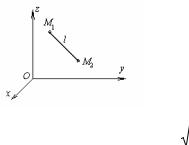
Приклад 1. Приведемо приклад утримуючої зв'язку. Нехай дві
|
матеріальні |
точки з'єднані один з одним за |
||||||||||||
|
допомогою |
абсолютно твердого |
стержня |
|||||||||||
|
довжиною l (мал.44). |
|
|
|
|
|
|
|
||||||
|
Як відомо з курсу аналітичної геометрії, |
|||||||||||||
|
відстань між двома |
|
точками визначається |
|||||||||||
|
за формулою |
|
|
|
|
|
|
|
|
|
||||
|
| M1M2 | = |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Мал.44 |
= (x |
2 |
− x )2 |
+ (y |
2 |
− y )2 + (z |
2 |
− z |
1 |
)2 , |
||||
|
|
|
|
1 |
|
1 |
|
|
|
|
||||
де xj , yj , zj − координати точки Mj |
(j = 1,2). |
|
|
|
|
|
|
|
|
|||||
Тоді математичне вираження стержня буде виглядати так |
|
|
|
|
|
|||||||||
тобто |
| M1M2 | = l , |
|
|
|
|
|
|
|
|
|
|
|
||
− x1)2 + (y2 − y1)2 + (z2 |
− z1)2 = l2 . |
|
|
|
|
|
|
|||||||
(x2 |
|
|
(161) |
|||||||||||
162

Таким чином, стержень являє собою приклад утримуючого зв'язку.
Приклад 2. Приведемо приклад неутримуючого зв'язку. Нехай тепер дві матеріальні точки з'єднані за допомогою нерозтяжної нитки, довжина якої дорівнює l (мал.45).
Очевидно, математичне вираження зв'язку в цьому випадку виглядає так
| M1M2 | ≤ l ,
чи
(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2 ≤ l2 . (162)
Таким чином, нитка є неутримуючим
зв'язком.
Мал.45
б) Зв'язки поділяються на стаціонарні і нестаціонарні. Стаціонарними називаються зв'язки, математичне вираження
яких не містить часу t явно. У протилежному випадку зв'язки
називаються нестаціонарними.
Очевидно, вищенаведені приклади зв'язків являють собою
стаціонарні зв'язки.
Приклад |
3. Приведемо приклад нестаціонарного зв'язку. Нехай |
переміщення |
точок M1,M2,…,Mп механічної системи обмежені знизу |
|
площиною П, висота якої h над |
|
координатною |
площиною |
хОу |
|
міняється з часом |
|
|
|
|
h = 2 t2 . |
|
|
Очевидно, математичне вираження |
||
|
зв'язку виглядає так |
|
|
|
zi ≥ 2 t2 |
(I = 1,2,…,n) |
(163) |
Мал.46 |
( zi – аплікати |
точок механічної сис- |
|
|
теми). Нерівності (163) показують, що |
||
площина П є нестаціонарним зв'язком.
в) Зв'язки поділяються на геометричні і кінематичні. Геометричними називаються зв'язки, що обмежують тільки
переміщення точок. У протилежному випадку (тобто коли зв'язки обмежують ще і швидкості точок) зв'язки називаються
163
кінематичними.
Ознакою геометричного зв'язку є відсутність похідних координат точок механічної системи за часом. Таким чином, усі вищенаведені приклади зв'язків є геометричними. Приведемо приклад кінематичного зв'язку.
Приклад 4. В автомобілі починаючого водія встановлено пристрій, що відключає двигун усякий раз, коли швидкість автомобіля досягає деякої заданої величини Vд. Таким чином, для швидкості автомобіля виконується нерівність
|
V ≤ Vд. |
(164) |
|
Вважаючи, що автомобіль є матеріальною |
точкою, що |
||
переміщається в площині хОу, нерівність (164) можна записати так |
|||
& 2 |
& 2 |
2 |
(165) |
x |
+ y |
≤ Vд , |
|
тобто в цьому випадку математичне вираження зв'язку містить похідні координат точки за часом.
§2. Ідеальні зв'язки
Зв'язки називаються ідеальними, якщо елементарна робота реакцій зв'язків на будь-якому нескінченно малому переміщенні механічної системи, що допускається цими зв'язками, дорівнює нулю.
Приклади ідеальних зв'язків.
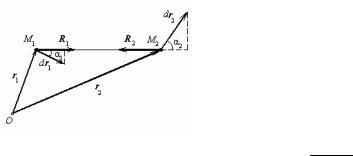
1.Стержень. Покажемо, що абсолютно твердий невагомий
стержень є ідеальним зв'язком. Нехай дві матеріальні точки М1 і М2 з'єднані за допомогою стержня. Реакції стержня R1 і R2 є прямопротилежними силами: R2 =
|
− R1. Очевидно, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
M1M2 = r2 − r1 |
|
(166) |
|||||
|
( rj |
− радіус-вектор |
|
|
точки Мj , |
|||||
|
j =1,2). Помножимо рівність (166) |
|||||||||
Мал.47 |
скалярно саме на себе |
|
|
|
||||||
|
(r |
− r , r |
− r ) =| M |
1 |
M |
2 |
|2 |
. (167) |
||
|
2 |
1 |
2 |
1 |
|
|
|
|
||
164
Оскільки стержень М1М2 абсолютно твердий, права частина рівності (167) є постійною величиною. Візьмемо диференціал від лівої і правої частин цієї рівності:
|
|
|
|
|
|
(r2 − r1, dr2 − dr1) = 0 |
|
|
|
|
|||||||||
чи якщо врахувати (166) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
(168) |
|||||||
|
|
|
|
|
(M1M 2 , dr1 ) − (M1M 2 , dr2 ) = 0 . |
|
|||||||||||||
Рівність (168) можна записати так |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 чи |
||
| M |
1 |
M |
2 |
|| dr | cos α |
1 |
− | M |
1 |
M |
2 |
|
|| dr |
2 |
| cos α |
2 |
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|dr1| cos α1 − |dr2| cos α2 = 0. |
|
|
(169) |
||||||||||||
Знайдемо елементарну роботу реакцій
(R1 , dr1) + (R2 , dr2) = (R1 , dr1) − (R1 , dr2) =
= R1 |dr1| cos α1 − R1 |dr2| cos α2 = R1 ( |dr1| cos α1 − |dr2| cos α2) = 0.
Таким чином, стержень є ідеальним зв'язком.
Помітимо, що абсолютно тверде тіло можна уявляти як сукупність матеріальних точок , попарно з'єднаних абсолютно твердими стержнями. Звідси випливає, що робота внутрішніх сил на будь-якім
переміщенні тіла дорівнює нулю.
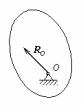
2. Нерухомий циліндричний шарнір без тертя. Нехай до тіла прикріплений нерухомий циліндричний шарнір (мал.48). Як відомо з
курсу статики, реакція шарніра проходить через вісь шарніра. Тому елементарна робота реакції RO шарніра
d = (RO , dro) = 0,
оскільки вісь шарніра нерухома і dro дорівнює нулю. Таким чином, нерухомий циліндричний шарнір є
ідеальним зв'язком.
Мал.48 Зовсім аналогічно можна довести, що нерухомий сферічний шарнір є ідеальним зв'язком.
3. Абсолютно тверда ідеально шершава поверхня.
Нехай по такій поверхні котиться абсолютно тверда каток (мал.49).
165

|
Оскільки прослизання в точці |
|
дотику Р катка і поверхні відсутнє, |
|
те переміщення drp точки Р катка |
|
дорівнює нулю і робота реакції |
|
d = (R , drp ) = 0, |
|
тобто абсолютно тверда ідеаль- |
Мал.49 |
но шершава поверхня є ідеальним |
|
зв'язком. |
§3. Принцип можливих переміщень (принцип Лагранжа)
Нескінченно малі переміщення механічної системи, що допускаються миттєво зупиненими зв'язками, називаються можливими.
Якщо зв'язки, накладені на механічну систему стационарні, то можливими є нескінченно малі переміщення, що допускаються
цими зв'язками.
Можливі переміщення точок системи будемо позначати символом δrk (k = 1,2,…,n)...
Теорема (принцип можливих переміщень). Для того щоб механічна система, підлегла ідеальним, стаціонарної, геометричним, утримуючим зв'язкам, знаходилася в рівновазі, необхідно і досить, щоб швидкості точок системи в початковий момент дорівнювали нулю і сума елементарних робіт активних сил на будь-якому можливому переміщенні дорівнювала нулю, тобто
n |
|
Vk (0) = 0 (k= 1,2,…,n), δA = ∑(Fk , δrk ) = 0 ... |
(170) |
k=1
Доказ.
Необхідність. Вищевказана механічна система знаходиться в рівновазі, необхідно довести, що виконано умови (170). Очевидно, що рівність нулю швидкостей виконана. Переконаємося, що виконано і друга умова (170). Кожна з точок системи знаходиться в рівновазі,
166
отже, виконані рівності |
|
Fk + Rk = 0 (k = 1,2,…,n). |
(171) |
Тут Fk − сума активних сил, що діють на точку Мk , Rk − сума реакцій
зв'язків, прикладених до |
цієї |
точки. Надамо |
системі можливе |
переміщення, при якому кожна з |
точок одержує переміщення δrk . |
||
Помножимо скалярно кожне з рівностей (171) на δrk |
і просумуємо по |
||
всіх точках системи. У результаті будемо мати |
|
||
n |
n |
|
|
∑(Fk , δrk ) + ∑(Rk , δrk ) = 0 . |
(172) |
||
k=1 |
k=1 |
|
|
Оскільки зв'язку, накладений на систему ідеальні, друга сума в лівій частині (172) дорівнює нулю, і з (172) випливає (170).
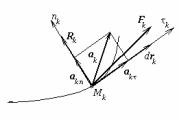
Достатність. Допустимо, що незважаючи на виконання умов (170), система почала рухатися. При цьому кожна з точок одержує переміщення drk . Направимо вісь τk уздовж напрямку цього вектора. Оскільки в початковий момент швидкості точок дорівнювали нулю, а зв'язки, накладені на систему стаціонарні і геометричні, то припущення про те, що система почала рухатися означає, що швидкість точки Mk починає зростати, а отже, дотичне прискорення точки
|
akτ |
= |
dVkτ |
|
> 0. |
|
|
dt |
|
||||
|
|
|
|
|
||
Тоді |
|
|
|
|
|
|
(ak |
, drk ) = (akτ |
, drk ) > 0. |
(173) |
|||
|
|
|
За третім законом динаміки |
|
||
|
|
|
|
|
mk ak = Fk + Rk . |
|
|
|
|
З (173) випливає |
|
||
|
|
|
(Fk + Rk , drk ) = mk (ak , drk ) > 0. |
|||
Мал.50 |
|
|
Підсумовуючи ці рівності по всіх |
|||
|
|
|
точках системи, одержуємо |
|
||
n |
|
|
n |
|
|
|
∑(Fk , drk ) + ∑(Rk , drk ) > 0 . |
(174) |
|||||
k=1 |
|
|
k=1 |
|
|
|
167

Оскільки зв'язки, накладені на систему ідеальні, друга сума у вираженні (174) дорівнює нулю, і в результаті будемо мати
n
∑(Fk , drk ) > 0 ,
k=1
що суперечить умові (170), оскільки переміщення точок drk (k = = 1,2,…,n) не суперечать накладеним зв'язкам, і виходить, утворяють можливе переміщення системи. Таким чином, наше припущення про те, що система почала рухатися невірно, і система знаходиться в стані рівноваги.
§4. Приклад рішення задачі з використанням принципу можливих переміщень
Задача. Плоский механізм, зображений на мал.51, знаходиться
в стані рівноваги під дією сили Q і пари сил з моментом М. Необхідно знайти момент пари, якщо Q = 2 кН , l1 = 2 м , l2 = 3 м , α = 30о.
Рішення. Надаємо механізму можливе переміщення, при якому кривошип О1А повертається на нескінченно малий кут δφ1 навколо
точки О1, а кривошип О1В − на кут δφ2 навколо |
точки О2 . На цьому |
переміщенні сила Q і сили, що утворять пари М, виконують наступну |
|
роботу |
|
M δφ1 − Q cos α l2 δφ2 = 0. |
(175) |
Для того щоб знайти залежність між δφ1 і δφ2 розглянемо переміщення стержня АВ. Переміщення його кінців показані на кресленні, причому
δА = l1 δφ1 , δУ = l2 δφ2 . (176)
Оскільки нескінченно малі переміщення точок пропорційні їх швидкостям і мають ті ж напрямки, то
Мал.51 δА і δУ пропорційні відстаням РА і РВ точок А и В від миттєвого цент-
ра обертання Р:
δА / δУ = РА / РВ = tg α . |
(177) |
168
З (176) і (177) знаходимо
δφ2 = δφ1 l1 / (l2 tg α).
Підставляючи це в (175), одержуємо
М = Q l1 cos2 α / sin α = 6 кНм.
§5. Визначення реакцій зв'язків за допомогою принципу можливих переміщень
У рівнянні робіт (170) принципу можливих переміщень реакції зв'язків узагалі не приймають участі.
Тому для визначення реакцій за допомогою принципу можливих
переміщень використовується спеціальний метод:
1)відкидаємо зв'язок, реакцію якого необхідно визначити;
2)дія відкинутого зв'язку заміняємо силою, що дорівнює шуканої реакції;
3)надаємо системі з відкинутим зв'язком можливе перемі-
щення;
4)обчислюємо суму робіт активних сил, включаючи додану, на цьому переміщенні;
5)з отриманого рівняння знаходимо додану силу і тим самим
визначаємо реакцію зв'язку.
Продемонструємо визначення реакції на прикладі.
Задача. Визначити реакцію шарнірно-рухливої опори В рами, зображеної на мал.52, Q1 = 20 кН , Q2 = 40 кН , М = = 40 кНм, а = 2 м, α = 45о. Зв'язки, накладені на раму, виключають можливість будь-якого переміщення.
Рішення.
1.Відкидаємо шарнірно-рухливу опору В и одержуємо конструкцію, що має можливість рухатися, тобто механізм (мал.53).
2.Дія відкинутого зв'язку заміняємо силою RB , що для механізму є активною.
Надаємо механізму можливе переміщення, при якому ліва части-
на рами повертається на нескінченно малий кут δφ1 навколо нерухомого шарніра А. При цьому шарнір D, що з'єднує дві частини рами, одержує переміщення δD, перпендикулярне відрізку AD,
169

що з'єднує його з центром обертання А. Шарнір С має можливість переміщатися
|
|
уздовж |
|
|
похилої |
площини, |
тому |
|||||||
|
|
можливе переміщення δC точки С |
||||||||||||
|
|
спрямовано уздовж її. Піднесемо |
||||||||||||
|
|
перпендикуляри до переміщень δD |
||||||||||||
|
|
і δC |
|
і на їхньому |
перетинанні |
|||||||||
|
|
знаходимо положення |
миттєвого |
|||||||||||
|
|
центра |
|
обертання, |
|
|
навколо |
якого |
||||||
|
|
права |
частина рами повертається |
|||||||||||
|
|
на нескінченно малий кут δφ2. |
||||||||||||
|
Мал.52 |
Співвідношення між δφ1 і δφ2 |
легко |
|||||||||||
|
|
знайти, виразивши через них δD: |
||||||||||||
|
|
δD = AD δφ1 = PD δφ2 , |
|
|
|
|
|
|
||||||
|
|
відкіля знаходимо |
|
|
|
|
|
|
||||||
|
|
δφ2 |
= |
|
AD |
δφ1 = |
2a |
δφ1 = 2δφ1 . |
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
PD |
a |
|
|
|
|
||||
|
|
3. |
|
|
Складаємо рівняння робіт |
|||||||||
|
|
активних сил, включаючи RB , на |
||||||||||||
|
|
цьому переміщенні |
|
|
|
|
||||||||
|
|
(RB a − Q1 2a) δφ1 − M δφ2 = 0. |
||||||||||||
|
Мал.53 |
З огляду на співвідношення між |
||||||||||||
|
|
δφ1 і δφ2, одержуємо |
|
|
|
|
||||||||
|
|
RB a − Q1 2a − 2M = 0. |
|
|
|
|
(178) |
|||||||
4. |
З рівняння (178) знаходимо RB |
= |
|
2(Q1a + M ) |
= 80 кН. |
|
||||||||
|
|
a |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
§6. Принцип Даламбера
Вектор J, рівний за модулем добутку маси точки на її прискорення і спрямований протилежно прискоренню, називається силою інерції точки:
J = − ma. |
(179) |
170
