
big_doc_LKG
.pdf
Випадкові процеси та їх статистичні характеристики |
169 |
(3.5)
Функція 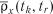 є аналогічною кореляційній функції і визначає ступінь зв’язку між елементами
є аналогічною кореляційній функції і визначає ступінь зв’язку між елементами  рядків і
рядків і  стовпців вихідної табл. 3.2, де відображено
стовпців вихідної табл. 3.2, де відображено  реалізацій неперервного випадкового процесу в дискретні моменти часу
реалізацій неперервного випадкового процесу в дискретні моменти часу 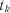 (
(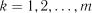 ). Однак ця функція також характеризує випадковий процес, так як для кожної пари дискретних значень аргументів
). Однак ця функція також характеризує випадковий процес, так як для кожної пари дискретних значень аргументів  вона дорівнює коефіцієнту кореляції і
вона дорівнює коефіцієнту кореляції і 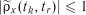 .
.
Головна діагональ матриці нормованої кореляційної функції містить всі одиниці, а по аналогії з кореляційним моментом, матриця симетрична відносно цієї діагоналі. Матриця має наступний вигляд
. (3.6)
Після того як обчислені оцінки числових характеристик  ,
,
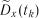 ,
, 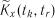 або
або 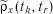 для значень аргументу
для значень аргументу  ,
,  , ...,
, ..., 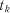 , ...,
, ..., 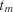 , можна побудувати відповідні графіки. Всі ці функції у разі необхід-
, можна побудувати відповідні графіки. Всі ці функції у разі необхід-
ності можна апроксимувати відповідними аналітичними виразами.
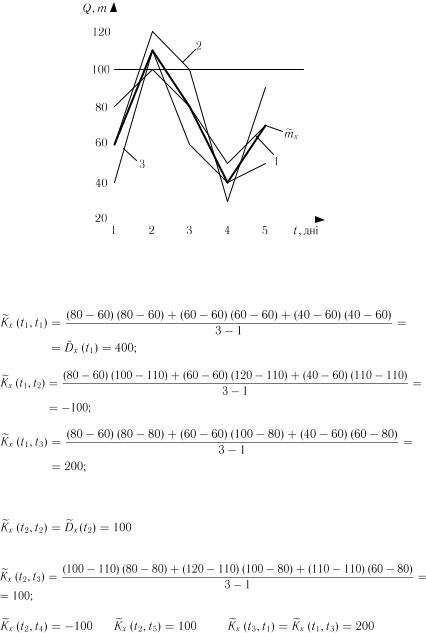
Приклад 1. В табл. 3.3 наведені дані про щоденні обсяги поставок споживачам зі складу металопрокату трьох видів продукції (П1–П3) протягом тижня (Т = 5 робочих днів). Необхідно визначити числові характеристики цього випадкового процесу.
Розв’язок. Випадковий процес 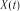 зводиться до системи трьох випадкових величин, що відповідають перерізам з інтервалом
зводиться до системи трьох випадкових величин, що відповідають перерізам з інтервалом  день, тобто
день, тобто  ,
, 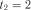 ,
, 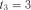 ,
,  ,
,  . Обчислюємо імовірнісні характеристики процесу за формулами
. Обчислюємо імовірнісні характеристики процесу за формулами
(3.1) та (3.2).


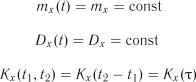
Випадкові процеси та їх статистичні характеристики |
173 |
суттєвих змін за перебігом часу. Такі випадкові процеси називаються стаціонарними. Прикладом стаціонарного випадкового процесу може бути кількість вантажів, що перевозиться транспортним засобом за одну їздку.
В протилежність стаціонарним, нестаціонарні випадкові процеси розвиваються у відповідності з певною тенденцією і суттєво змінюються у часі. Характеристики такого процесу залежать від вибору початку відліку часу.
Для більшості динамічних систем випадкові процеси починаються з
нестаціонарної стадії, яка надалі переходить у сталий режим, а
випадкові процеси, що відбуваються в ній, можна вважати стаціонарними. Прикладом нестаціонарного випадкового процесу є зміна відносних значень величини пасажиропотоку за часом протягом доби. Спочатку пасажиропотік зростає (t = 7 – 9 год.), потім дещо спадає (t = 9 – 10 год.), стабілізується (t = 10 –14 год.), збільшується (t = 15 – 18 год.), і , нарешті, спадає (t = 18 – 24 год.). Цей процес у деякому проміжку часу (наприклад, в інтервалі t = 10 – 14 год.) приблизно може бути прийнятим як стаціонарний.
Випадковий процес 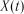 називається стаціонарним, якщо його
називається стаціонарним, якщо його
математичне очікування 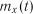 і дисперсія
і дисперсія 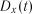 мають однакові значення у всіх точках числової осі, а кореляційна функція
мають однакові значення у всіх точках числової осі, а кореляційна функція 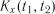 залежить тільки від величини інтервалу
залежить тільки від величини інтервалу 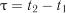 між двома точками
між двома точками  і
і 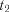 , і не залежить від його розташування на числовій осі, тобто
, і не залежить від його розташування на числовій осі, тобто
; |
(3.7) |
; |
(3.8) |
. |
(3.9) |
Так як 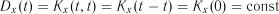 , то єдиною суттєвою умовою стаціонарності є залежність кореляційної функції від інтервалу
, то єдиною суттєвою умовою стаціонарності є залежність кореляційної функції від інтервалу  змінювання аргументів.
змінювання аргументів.
Таким чином, кореляційна функція стаціонарного випадкового процесу залежить не від обох аргументів  і
і 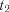 , а тільки від різниці між ними
, а тільки від різниці між ними  , тобто є функцією не двох, а лише одного аргументу.
, тобто є функцією не двох, а лише одного аргументу.
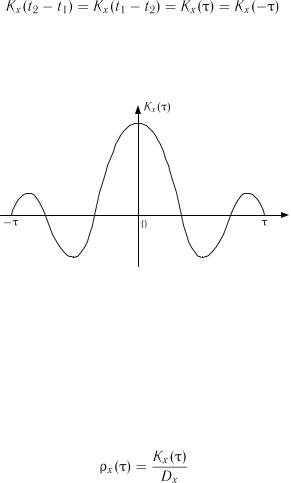
Кореляційна функція будь-якого випадкового процесу має властивість симетрії, тобто

Випадкові процеси та їх статистичні характеристики |
175 |
Кореляційна функція стаціонарного випадкового процесу характеризує внутрішню структуру процесу у часовій області. Процес називається строго стаціонарним, якщо його властивості не залежать від моменту початку відліку. В термінах функцій розподілу це означає, що якщо усі моменти часу зсунути на один і той же інтервал часу 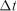 , то спільна функція розподілу не змінюється, тобто
, то спільна функція розподілу не змінюється, тобто
. (3.11)
Виходячи із умови стаціонарності, можна записати
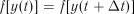 .
.
Оскільки ми не фіксували величину 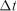 , то можна зробити висновок, що для стаціонарного процесу функція розподілу
, то можна зробити висновок, що для стаціонарного процесу функція розподілу  буде постійною, тобто не буде залежати від часу. Позначимо її
буде постійною, тобто не буде залежати від часу. Позначимо її 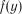 . Тоді стаціонарний процес має постійне середнє значення
. Тоді стаціонарний процес має постійне середнє значення
(3.12)
і постійну дисперсію
. (3.13)
Все це виправдовує наявність стаціонарності стохастичного процесу, тобто це процес, який з постійною дисперсією флуктуює (коливається) навколо свого середнього значення.
3.2.2. Способи встановлення стаціонарності випадкового проце-
су. Випадковий процес може бути стаціонарним в середньому і в дисперсії. У деяких випадках перевірка стаціонарності функції розподілу не потрібна, так як просте зображення її на графіку показує, що функ-
ція або зростає, або спадає, або має коливання зі змінною амплі-
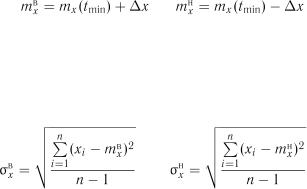

Випадкові процеси та їх статистичні характеристики |
177 |
5. Ідентифікують властивості стаціонарності чи нестаціонарності: якщо значення 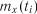 укладаються в інтервал
укладаються в інтервал  , тоді про-
, тоді про-
цес вважається стаціонарним за середнім значенням  ;
;
якщо всі значення  укладаються в інтервал
укладаються в інтервал  , тоді про-
, тоді про-
цес вважають стаціонарним за дисперсією 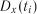 ;
;
якщо хоча б одне значення 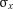 не укладається в інтервал
не укладається в інтервал  ,
,
процес визначають як нестаціонарний, навіть якщо величина середнього арифметичного 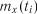 не змінюється в часі.
не змінюється в часі.
Спосіб 2. Вихідні дані представляються статистичними вибірка-
ми спостережень. В практиці досліджень використовуються декілька методів перевірки процесу на стаціонарність.
Безпосередня перевірка умов стаціонарності.
Для вибраних перерізів 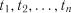 випадкового процесу
випадкового процесу 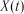 розраховуються характеристики
розраховуються характеристики 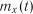 ,
, 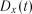 ,
, 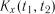 і перевіряється виконання умов стаціонарності (3.7) та (3.8).
і перевіряється виконання умов стаціонарності (3.7) та (3.8).
Приклад 1. Досліджується процес доставки дрібнопартіонних вантажів з центральної матеріальної бази постачання. Щодобово (інтервал спостережень  ) фіксувався обсяг поставок п`ятьом споживачам (кількість реалізацій) протягом
) фіксувався обсяг поставок п`ятьом споживачам (кількість реалізацій) протягом 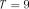 діб. Результати спостережень представлені в табл. 3.5.
діб. Результати спостережень представлені в табл. 3.5.
Таблиця 3.5 Експериментальні дані обсягу поставок  за дев’ять діб поточного періоду
за дев’ять діб поточного періоду
Номер |
|
|
|
Період часу |
, доби |
|
|
|
||
реалізації |
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
35 |
35 |
35 |
36 |
37 |
35 |
34 |
32 |
37 |
|
|
35 |
35 |
36 |
36 |
35 |
35 |
35 |
35 |
35 |
|
|
32 |
34 |
32 |
34 |
33 |
32 |
31 |
31 |
32 |
|
|
31 |
31 |
31 |
31 |
31 |
31 |
31 |
31 |
31 |
|
|
33 |
31 |
30 |
30 |
30 |
28 |
29 |
28 |
30 |
|
|
|
|
|
|
|
|
|
|
|
|
Розв’язок.
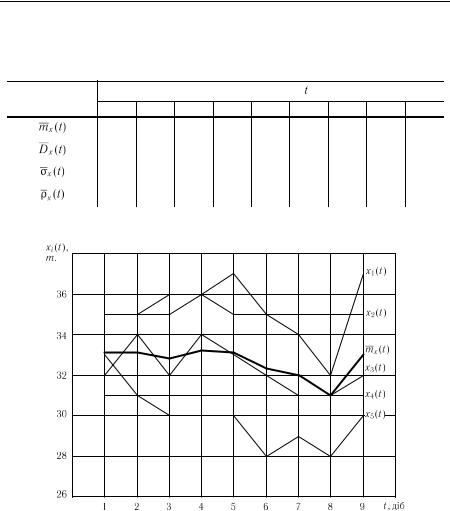
1. Обчислюємо оцінку математичного очікування 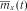 . Для цього підсумовуємо значення, наведені в табл. 3.5, по стовпчиках і ділимо отриману суму на кількість реалізацій, тобто на 5. Отримані результати занесемо в табл. 3.6 і на її підставі побудуємо графік (рис. 3.5) величини
. Для цього підсумовуємо значення, наведені в табл. 3.5, по стовпчиках і ділимо отриману суму на кількість реалізацій, тобто на 5. Отримані результати занесемо в табл. 3.6 і на її підставі побудуємо графік (рис. 3.5) величини 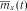 .
.
178 |
|
Розділ 3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
Таблиця 3.5 |
||
Імовірнісні характеристики випадкового процесу |
|
|
|||||||
|
доставки дрібнопартіонних вантажів |
|
|
|
|||||
Характеристики |
|
|
Періоди часу |
|
|
|
|||
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
||
1 |
|||||||||
33,20 |
33,20 |
32,80 |
33,40 |
33,20 |
32,20 |
32,00 |
31,40 |
33,00 |
|
3,20 |
4,10 |
6,70 |
7,80 |
8,20 |
8,70 |
6,00 |
6,30 |
8,50 |
|
1,80 |
2,02 |
2,60 |
2,80 |
2,86 |
2,95 |
2,45 |
2,50 |
2,92 |
|
1,00 |
0,89 |
0,91 |
0,84 |
0,89 |
0,83 |
0,81 |
0,71 |
0,81 |
|
Рис. 3.5. Графіки випадкового процесу |
|
|
|
||||||
|
доставки дрібнопартіонних вантажів |
|
|
|
|||||
2. Обчислюємо оцінку дисперсії  . Щоб спростити обчислення оцінок дисперсії, виконаємо центрування випадкового процесу, тобто віднімемо від кожного елемента стовпчиків табл. 3.5 відповідне йому математичне очікування і отримані результати представимо в табл. 3.7.
. Щоб спростити обчислення оцінок дисперсії, виконаємо центрування випадкового процесу, тобто віднімемо від кожного елемента стовпчиків табл. 3.5 відповідне йому математичне очікування і отримані результати представимо в табл. 3.7.

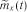 та
та 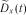 зведені у табл. 3.4.
зведені у табл. 3.4.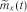 , обчислюємо кореляційну функцію для різних пар значень аргументу:
, обчислюємо кореляційну функцію для різних пар значень аргументу: 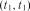 ,
, 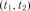 ,
,  , ...,
, ...,  , ...,
, ...,  ,
, 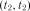 ,
,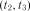 , ...,
, ..., 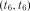 за формулою (3.3).
за формулою (3.3).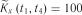 ;
; 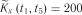 ;
; 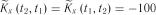 ;
;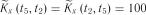 ;
; 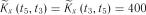 ;
; ;
;  .
.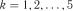 ;
; 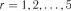 .
.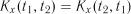 .
. , а при побудові графіка від`ємні значення аргументу можна не зображувати. При розв`язуванні практичних задач замість кореляційної функції
, а при побудові графіка від`ємні значення аргументу можна не зображувати. При розв`язуванні практичних задач замість кореляційної функції 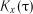 часто користуються
часто користуються 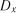 – постійна дисперсія стаціонарного випадкового процесу. Величина
– постійна дисперсія стаціонарного випадкового процесу. Величина  представляє собою коефіцієнт кореляції між
представляє собою коефіцієнт кореляції між  за часом. Очевидно, що
за часом. Очевидно, що  .
.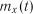 і дисперсії
і дисперсії 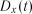 . Основні підходи до ідентифікації властивості стаціонарності визначаються способами отримання вихідних даних.
. Основні підходи до ідентифікації властивості стаціонарності визначаються способами отримання вихідних даних.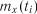 .
. ,
, 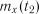 , ...,
, ..., 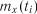 вибирають мінімальне значення
вибирають мінімальне значення 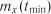 і будують інтервали з межами
і будують інтервали з межами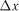 – точність методики вимірювання досліджуваного показника.
– точність методики вимірювання досліджуваного показника.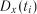 і стандартне відхилення
і стандартне відхилення 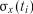 для тих же моментів часу.
для тих же моментів часу. – кількість спостережень.
– кількість спостережень.