Photochemistry_of_Organic

bond length re and a well depth De. The so-called potential energy includes not only the potential energy of the nuclei and electrons, but also the kinetic energy of the latter. The total energy including nuclear kinetic energy is represented by horizontal lines (v ¼ 0 for the lowest vibrational level). The PESs of molecules with more than two nuclei, N > 2, are difficult to visualize. They are frequently shown as twoor, at best, three-dimensional cuts along one or two relevant’ internal coordinates through their (3N 6)-dimensional space. This should always be kept in mind, because such pictures can be misleading.

As a result of the BO approximation, wavefunctions can be factored into the product of an electronic wavefunction, C0el, and a vibrational wavefunction, x. Rotational states are not considered here, because they are not resolved in solution spectra.

C C0elðqel; qnuclÞxðqnuclÞ

Equation 1.6 Separation of electronic and vibrational wavefunctions

The vibrational wavefunction depends only on the nuclear coordinates qnucl. The nuclei move in a fixed electronic potential that is often approximated as a harmonic potential (dashed curve in Figure 1.10) to determine vibrational wavefunctions near the potential’s bottom. The electronic wavefunction carries the complete information about the motion and distribution of electrons. It still depends on both sets of coordinates qel and qnucl, but the latter are now fixed parameters rather than independent variables; the nuclei are considered to be fixed in space. The BO assumption is a mild approximation that is entirely justified in most cases. Not only does it enormously simplify the mathematical task of solving Equation 1.5, it also has a profound impact from a conceptual point of view: The notions of stationary electronic states and of a PES are artefacts of the BO approximation. It does break down, however, when two electronic states come close in energy and it must be abandoned for the treatment of radiationless decay processes (see Section 2.1.5).

Magnetic fields in molecules arise from three sources: the motion of charges in space, electronic spin and nuclear spin. The last two are fundamental properties of electrons and some nuclei, which have no classical analogy. So far, we have ignored the magnetic interactions operating in molecular systems altogether. They were not even mentioned as contributions to the potential energy part of the Hamiltonian operator (Equation 1.5), because they are much weaker than the Coulombic terms dealt with. However, magnetic interactions are the only driving force for photophysical processes that involve a change in multiplicity, so they must be considered explicitly to deal with such processes (Section 4.8). Moreover, we shall see below that the symmetry of electronic spin functions must always be treated explicitly, because of its strong impact on the distribution of electrons via the Pauli principle.

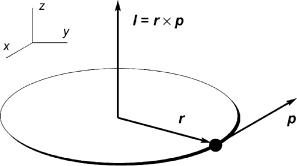
In classical mechanics, the angular momentum l of a mass point running on a circular orbit is defined by the vectore l ¼ r p (Figure 1.11), which has an orientation in space that

e Vectors have a magnitude and a direction; in this text, the symbols for vector quantities (and matrices, Section 3.7.5) are printed in bold italics. In a Cartesian coordinate system, a vector a is fully defined by its components ax, ay and az, the projections of a onto the Cartesian axes. The length or magnitude of a is given by the Pythagorean expression a ¼ jaj ¼ ða2x þ a2y þ a2z Þ½. Two vectors of equal length and direction are equal, independent of their position in space. The sum (or difference) of two vectors is defined by the sum (or difference) of their components, a b ¼ c, cx ¼ ax bx, etc. The scalar product of two vectors is designated ab and is a scalar; ab ¼ abcosw, where w is the smaller angle enclosed by a and b. The vector product (or cross product), designated a b, is a vector c of length c ¼ absinw, which equals the area of the parallelogram spanned by a and b. The vector c is perpendicular to the plane spanned by a and b and points in the direction given by the right-hand rule (the direction of the thumb, if the index of the right hand is rotated from a to b through the angle w).

Figure 1.11 Angular momentum I of a mass point running on a circular orbit

may be defined by its components in a Cartesian coordinate system, ‘x, ‘y and ‘z, and a length ‘ ¼ mvr ¼ ð‘2x þ ‘2y þ ‘2z Þ1=2, the magnitude of the angular momentum.

As the energies of electrons in atomic orbitals are quantized, so are their angular momenta. The quantum of angular momentum is h ¼ h=2p. Only one component of the vector l of angular momentum can be specified precisely. The atomic orbitals (Figure 1.9) obtained by solution of the Schro¨dinger equation are thus specified by two quantum numbers, the orbital angular momentum quantum number l and the angular momentum quantum number ml of one component, arbitrarily chosen to be the z-component. The quantum number l is a non-negative integer and for a given value of l there are 2l þ 1 permitted values of ml (Equation 1.7). The quantum number l ¼ 0 is associated with

A classical analogy for visualizing the quantization of m is that of a spinning top in the gravitational field. In response to gravity, the top does not fall down, but precesses around the axis of the force, the spin axis sweeping out a conical surface. The response of an electron in an orbital with l 6¼0 to an external magnetic field H along the z-axis will be similar: the orbital magnetic moment m will precess around the z-axis. The fundamental difference is that the projection of the magnetic moment on to the z-axis is allowed to assume only the discrete set of values ml defined by Equation 1.7.

The electron spin angular momentum quantum number is restricted to the value s ¼ 1=2, so that analogously to Equation 1.7 (replace l by s and ml by ms), electron spin can take only two orientations with respect to the z-axis, specified by the spin magnetic quantum numbers ms ¼ þ 1=2 (spin up’, ") and ms ¼ – 1=2 (spin down’, #). Stern and Gerlach first demonstrated the existence of the electron spin magnetic moment by passing a beam of silver atoms through an inhomogeneous magnetic field. Silver atoms have a single

unpaired electron, so that the beam separates into two components, one for atoms with ms ¼ þ 1=2 and the other for ms ¼ – 1=2.

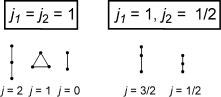
The allowed quantum numbers of total angular momentum j that can arise from a system of two sources of angular momentum with quantum numbers j1 and j2 are defined by the series given in Equation 1.8.

j ¼ j1 þ j2; j1 þ j2 1; . . . ; j j1 j2j

Equation 1.8 Combination of angular momentum quantum numbers

A pictorial representation of Equation 1.8 is shown in Figure 1.12. Given two sticks of length j1 and j2, the task is to join them with a third stick of length j in all possible ways to form triangles. The length j of the third stick has to start at length j1 þ j2 and can be reduced only in unit steps. Note that triangles’ with lengths j ¼ 0 or j ¼ j1 þ j2 are permitted.

Figure 1.12 Vectorial addition of angular momenta

Lower-case letters are used to label the quantum numbers for orbitals (s for electronic spin, l for orbital angular momentum and j for total angular momentum) and capital letters (S for total electronic, L for total orbital and J for total angular momentum) to label the overall state of an atom or molecule. For example, the total angular momentum of a p-electron (s ¼ 1=2, l ¼ 1) can have the values j ¼ s þ l ¼ 3=2 and j ¼ s þ l 1 ¼ |s l | ¼ 1=2, so for an atom with a single p-electron J can take the values 3=2 and 1=2.

When there are two electrons in a molecule, their total spin angular momentum quantum number S is given by Equation 1.9.

S ¼ s1 þ s2; s1 s2 ¼ 1;0

Equation 1.9 Total spin angular momentum for two electrons

If there are three electrons, S (a non-negative integer or half integer) is obtained by coupling the third spin to S ¼ 1 and S ¼ 0 for the first two spins, giving S ¼ 3=2, 1=2 and 1=2, and so on for more electrons. When all electron spins in a molecule are paired (# "), the total electronic spin quantum number S is 0; there is no net electronic spin. Radicals with a single unpaired electron have S ¼ 1/2. For a system with two unpaired electron spins, S ¼ 1. A state with S ¼ 0 can have only one value of MS, MS ¼ 0, and is a singlet. A state with S ¼ 1 can have any of the three values MS ¼ 1, 0 or 1 (Equation 1.7) and is a triplet. The multiplicity M of a state is equal to 2S þ 1. Thus, for S ¼ 0 the multiplicity is 1 (singlet state), for S ¼ 1/2 it is 2 (doublet state) and for S ¼ 1 it is 3 (triplet state). The multiplicity indicates the number of distinct magnetic sublevels belonging to an

electronic state. The multiplicity of molecular species is commonly shown as an upper left index, e.g. 3O2 and 2NO for dioxygen in the triplet ground state and for the NO radical, respectively. In photochemistry, the labels S1 and T1 are also used to designate the lowest excited singlet and triplet state of molecules with an even number of electrons (see Section 2.1.1). The interaction of electron spin with the orbital magnetic moment (spin–orbit coupling, SOC) must be considered to calculate the rates of photophysical processes involving a change of multiplicity, which play a dominant role in photochemistry (Section 2.1.1; SOC will be discussed in Sections 2.1.6 and 5.4.4).

Provided that we do not consider magnetic interactions in the Hamiltonian operator explicitly, the electronic wavefunction C0el can be further separated into the product of the so-called space part Cel and a spin function s as shown in Equation 1.10 for a two-electron system (linear combinations of spin functions are needed for systems with more electrons). For a single electron, the spin function s ¼ a (or ") represents the state with ms ¼ 1/2 and the function b (or #) that with ms ¼ –1/2.

C Celðqel; qnuclÞxðqnuclÞs

Equation 1.10 Separation of electronic, vibrational and spin wavefunctions

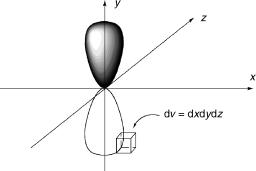
The spatial part of the wavefunction Cel (e.g. 2py, Figure 1.13) holds the information about the spatial distribution of the electrons surrounding fixed nuclear positions. Max Born first proposed that the square of the spatial wavefunction multiplied by a volume element dv, C2eldv, is equal to the probability of finding the electrons in that volume element dv. This is easily visualized for atomic orbitals containing a single electron; f2dv ¼ f2(x1,y1,z1)dxdydz is the probability of finding the electron in the volume element dv ¼ dxdydz surrounding a given position x1,y1,z1. For species with many electrons, C2eldv is the probability of finding one electron in a volume element around a defined position in space, x1,y1,z1, another at x2,y2,z2, and so on.

Figure 1.13 Spatial wavefunction of a 2py AO. The shading (filled/empty) denotes the change in sign of the wavefunction. The probability (2py)2dv is 0 throughout

The Born interpretation of C2el as a probability function requires that the wavefunction Cel be normalized, namely that integration of C2eldv over all space (Equation 1.11), equals

unity, because the system of electrons described by Cel must be located somewhere in space. Integration over all space requires multiple integration over the three coordinates for each of the n electrons, which is abbreviated as hCeljCeli.f Wavefunctions can always be normalized by dividing Cel by hCeljCeli.

ð ð ð ð ð ð ð

C2eldn ¼ . . . C2eldx1dy1dz1 . . . dxndyndzn ¼ hCeljCeli

Equation 1.11

The sublevels of an electronic state with multiplicity M > 1 are nearly degenerate, that is, they have nearly the same energy. Any small energy differences between the sublevels are due to the weak magnetic interactions within the molecule. The splitting increases in response to strong external magnetic fields.

The foremost impact of electronic spin is due to the Pauli principle, a fundamental postulate of quantum mechanics. It can be stated as follows: The total wavefunction (Equation 1.10) must be antisymmetric with respect to the interchange of any electron pair ei and ej, i.e. of their coordinates qei and qej (Equation 1.12).

Cð. . . qei ; . . . qej ; . . . ; qnÞ ¼ Cð. . . qej ; . . . qei . . . ; qnÞ

Equation 1.12 Antisymmetry of the total wavefunction

Wavefunctions must be either symmetric (delete the minus sign from Equation 1.12) or antisymmetric in order to be consistent with the Born interpretation: electrons being indistinguishable, C2 must be invariant with respect to an interchange of any pair of electrons, because the probability of finding ei in a volume element around the coordinates qei and ej around qej must be the same when the labels i and j are exchanged. Both symmetric and antisymmetric wavefunctions would satisfy this condition, but the Pauli principle allows only antisymmetric wavefunctions.

Electronic spin exerts a strong influence on the energies associated with wavefunctions as a consequence of the Pauli principle. Consider the factored wavefunction, Equation 1.10. The product of two symmetric or two antisymmetric functions is symmetric, that of a symmetric and an antisymmetric function is antisymmetric. The spin functions for twoelectron systems representing a singlet state (S ¼ 0) are antisymmetric; those representing a triplet state (S ¼ 1) are symmetric.18 Vibrational wavefunctions x(qnucl) are invariant with respect to electron exchange, i.e. symmetric, as they do not depend on the electronic coordinates. Therefore, the electronic wavefunction for the triplet state must be antisymmetric in order to satisfy the Pauli principle.

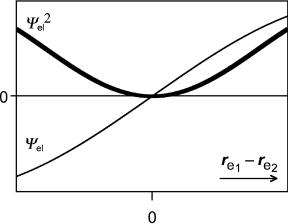
Now consider an electronic wavefunction Cel describing the distribution of two electrons in a triplet state. Because it is antisymmetric, it must change sign, when the

f Wavefunctions may be complex functions; Cel then defines a complex number a þ ib (i ¼ H 1) rather than a real one for each point in the multidimensional parameter space of the electronic coordinates. In that case C2el must be replaced by CelCel, where Cel is the complex conjugate of Cel (a þ ib is replaced by a – ib). In the shorthand notation hCeljCeli, the first wavefunction is understood to be the complex conjugate of the second.

Figure 1.14 Fermi hole

distance between the two electrons defined by the vector re1 re2 vanishes (Figure 1.14). The square of the wavefunction, C2el, must then have a broad minimum around that point. Two electrons with parallel spin can never be at the same point in space and, because Cel is a continuous function, they have a low probability of being near each other. This dip in the distribution of two electrons is called the Fermi hole. It has nothing to do with the Coulombic repulsion between the electrons that also operates to keep electrons apart. Rather, it functions somewhat like traffic lights that (ideally) prevent cars from crashing. Electronic wavefunctions for a singlet state are symmetric under electron exchange, so that the traffic rule does not apply. This is the basis of the first of Hund’s rules (see Section 4.1).

The Born interpretation also requires that wavefunctions be either symmetric or antisymmetric with respect to all symmetry operations of a molecule, that is, when the coordinates of all the electrons and nuclei are exchanged by symmetry-equivalent coordinates. For example, the electronic distribution around an isolated atom must be spherically symmetric in the absence of external fields.

Once an eigenfunction Cn has been determined, all observable properties of a system in that state are defined. The index n is a label to distinguish different solutions of Equation 1.5, which represent different states. For each observable property of a given state, there is

But how can we calculate the energy from approximate wavefunctions Fn Cn that are

^ unchanged? We can always multiply both sides of the approximate equation HFn EnFn

with n from the left: n ^ n n n n. On the right-hand side, we can replace n n n

F F HF F E F F E F

side, because H is a differential operator: FnH 6¼HFn. Integration of FnHFn EnFn

over all space yields Equation 1.13. For normalized wavefunctions Fn, hFnjFni ¼ 1. Most

Equation 1.13

Observables calculated from approximate wavefunctions as in Equation 1.13 are called expectation values, an expression used in probability theory. In practice, we will always have to be satisfied with approximate wavefunctions. How can we choose between different approximations? And if our trial wavefunction has adjustable parameters (such as the coefficients of atomic orbitals in molecular orbitals; see Section 4.1), how can we choose the adjustable parameters’ best values? Here, Rayleigh’s variation theorem is of great value. It tells us that the expectation value for the ground state energy E1, hE1i, calculated from an approximate wavefunction F1 is always larger than the true energy E1 (Equation 1.14). Proof of the variation theorem is given in textbooks on quantum mechanics.18

Equation 1.14 Variation theorem

Thus, the wavefunction giving the lowest eigenvalue E1 will be the best. Having defined a trial wavefunction F with adjustable parameters, we want to optimize it by determining those values of the parameters that give the lowest expectation value for the energy. If we use a trial function F that is a linear combination (LC) of an orthonormalg basis set, e.g. a set of orthonormal AOs fi (LCAO) (Equation 1.15),

where we require F to be normalized, <F|F> ¼ 1, then we must solve a set of simultaneous differential equations (qE=qciÞ ¼ 0, the secular equations, in order to find the best values of the coefficients ci. This is a well-known problem of linear algebra; nontrivial solutions (the trivial solution is a vanishing wavefunction; ci ¼ 0 for all i) exist

g The functions fi of the basis set are orthonormal, i.e. orthogonal, hfijfji ¼ 0 for i 6¼j and normalized, hfijfii ¼ 1, for all i.

The elements ij of Equation 1.16 represent the integrals h ij ^ j ji and the symbol ij

H

F

H

F

d used in the shorthand notation for the secular determinant on the left is Kronecker’s delta, which takes the value of 1 for i ¼ j and 0 otherwise, as can be seen from the extended notation on the right. Solving Equation 1.16 yields a set of energies En that are called the eigenvalues of the matrix (Hij dijE). The associated sets of coefficients cin, the eigenvectors, are then obtained by inserting each solution En into the secular equations. The corresponding eigenfunction Fn is given by Equation 1.15 with the coefficients defined by the eigenvector associated with En. An explicit example will be given in Section 4.3.

The same procedure can be used to calculate the interaction energy between two systems. Given the wavefunctions Cn and Cm for the isolated separate systems, we can use them as trial wavefunctions as in Equation 1.15 to determine the energies of the combined system. The probability of radiative or nonradiative transitions between zero-order BO

wavefunctions n and m is proportional to the square of the integrals h nj^ j mi, where

C C C O C

the operator ^ depends on the process considered (see Sections 2.1.4–2.1.6).

O

From a mathematical point of view, the task of finding (approximate) eigenfunctions of Equation 1.5 for a molecule is no more complicated than solving the Newtonian equations for a mechanical system with a similar number of bodies such as the solar system. An important difference is that the interactions between all particles in a molecule are of comparable magnitude, on the order of electronvolts (1 eV NA ¼ 96.4 kJ mol 1). In calculations of satellite trajectories or planetary movements, on the other hand, one can start with a small number of bodies (e.g. Sun, Earth, Moon, satellite) and subsequently add the interactions with other, more distant or lighter bodies as weak perturbations. This greatly simplifies the task of calculating a satellites’ trajectory.

Nevertheless, perturbation theory is also of great importance in quantum mechanics. The formidable task of solving the Schro¨dinger Equation 1.5 is simplified by removing

some particularly intractable terms from the Hamiltonian operator ^. Using eigenfunc-

H

tions of the simplified operator ^ 0, it is possible to estimate the eigenvectors and

H

hThe determinant of a square matrix A ¼ (Aij) of size n n (see footnote c in Section 3.7.5), denoted ||A||, is a number that is calculated from the elements Aij of the matrix by Laplacian expansion by minors (see textbooks of mathematics). The results for 1 1, 2 2 and 3 3 determinants are shown below.

A11 A12 A13

A21 A22 A23 ¼ A11A22A33 þ A12A23A31 þ A13A21A32 A12A21 A33 A11A23A32 A13A22A31

A31 A32 A33

operator.

Perturbation theory is also invaluable to predict trends in related series of compounds (substituent effects). To calculate the energy of benzene ab initio amounts to evaluating the energy released when six carbon nuclei, six protons and 42 electrons combine to form benzene, which is 6 105 kJ mol 1. The accuracy needed to predict chemical reactivity is on the order of 1 kJ mol 1 (a decrease of 1 kJ mol 1 in activation energy amounts to a 50% increase in the corresponding rate constant). This is reminiscent of the attempt to determine the weight of the captain by weighing the ship with and without the captain aboard. Perturbation theory evaluates the small energy difference between a pair of closely related compounds directly, making no attempt to calculate the parent system on an absolute scale. We shall make extensive use of perturbation theory in Chapter 4.

1.5 Problems

1.Calculate the energy of one mole of photons, l ¼ 400 nm. [Ep ¼ 300 kJ mol 1]

2.Determine the work function w for sodium metal (the energy needed to remove an electron from sodium metal) and the value of Planck’s constant h from Figure 1.5.

[w 1.84 eV, h 6.6 10 34 J s. Note: the first ionization potential of sodium, I1 ¼ 5.14 eV, refers to ionization of a sodium atom in the gas phase]

3.Name the colour of light of 400, 500 and 600 nm and of a light source emitting at both 490 and 630 nm with equal intensity. [Figure 1.8]

4.Name the colour of dyes with absorption maxima at 400 nm, at 500 nm and at both 400 and 600 nm (equal intensity). [Figure 1.8]

5.What are the advantages of the Born–Oppenheimer approximation and when is it necessary to go beyond? [Separation of electronic and vibrational wavefunctions, existence of PES; calculation of IC and ISC rate constants, near-degenerate states]

6.How many angular momentum quantum numbers j are possible for an electron in a d-orbital? [6]

7.Given the ground-state energies of atoms A and B, (a) EA ¼ 20 and EB ¼ 30 eV or

(b) EA ¼ EB ¼ 25 eV, and the matrix element for their interaction at a given distance,

h Aj ^ j Bi ¼ 1 eV, calculate the lowest eigenvalue (for cases a and b) of the combined

C H C

system A B. [(a) 30.1 eV, (b) 26 eV]

8.If plants exist on planets of other stars, their colour would probably be different from plants on Earth. Explain. [Ref. 21]