
Photochemistry_of_Organic
.pdf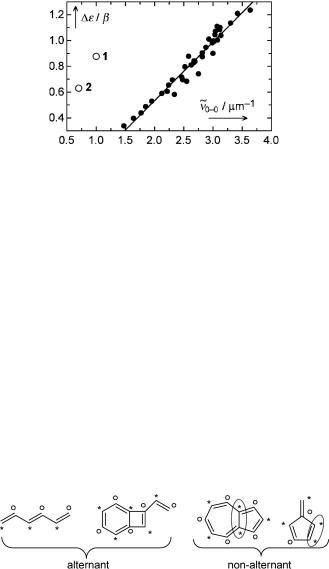
156 |
Quantum Mechanical Models |
Figure 4.17 Correlation of the p-band positions of benzenoid aromatic hydrocarbons with HMO HOMO–LUMO gaps. Data taken from ref. 282, except for the outliers azulene (1) and cycl[3.3.3]azine (2) that do not belong to the same class of compounds
showed that their assumed structure had been incorrect.283 It is amazing that the structural identiÞcation of some of the higher members of these polynuclear hydrocarbons relies entirely (yet convincingly) on their electronic and photoelectron spectra. For example, an earlier X-ray structure of ÔcircumanthraceneÕ was shown to be incorrect, because the crystals are strongly disordered.283
4.6 Pairing Theorems and Dewar s PMO Theory
Recommended reading.284,285
Conjugated hydrocarbons that do not contain an odd-membered ring are called alternant hydrocarbons (AHs). The distinction between alternant and non-alternant hydrocarbons (NAHs) provides a very important classiÞcation of conjugated hydrocarbons, especially with regard to excited states. In AHs, the unsaturated C atoms can be assigned to two sets, the starred ( ) and the unstarred (o) set, such that no atoms of the same set are bound to each other. This is not possible for NAHs (Figure 4.18).
Figure 4.18 Alternant and non-alternant hydrocarbons
Coulson and Rushbrooke have derived several theorems and corollaries for AHs,286 which may be summarized as follows:
1.HMOs with «j 6¼a (xj 6¼0) occur in pairs with energies « j ¼ a xjb. The HMOs of buta-1,3-diene serve as an example. Note that orbital pairing remains intact when a bonding perturbation is introduced between atoms 1 and 4 (Figure 4.6), but not when an inductive perturbation is introduced (Figure 4.5). The HMO-coefÞcients cjm of paired
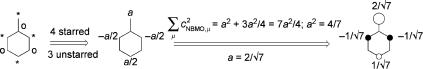
|
|
Pairing Theorems and Dewar’s PMO Theory |
157 |
||||||
MOs («j o6¼a) |
o |
* |
* |
jm |
¼ |
|c |
jm |
|, but they change sign on one set, |
|
|
are numerically the same, |c |
| |
|
|
|||||
that is, cjm ¼ c jm and cjm ¼ c jm. Whether the sign is changed in the starred or the unstarred set is irrelevant, because wavefunctions of opposite sign are equivalent. Thus, the energies and HMO coefÞcients of a bonding orbital cj and its paired antibonding orbital c j are related through Equation 4.23 (cf. e.g. Figure 4.6).
XX
cj ¼ cojmfom þ c*j f*n «j ¼ a þ xj b mo n*
XX
c j ¼ mo |
cjomfmo n* |
cj*fn* « j ¼ a xj b |
Equation 4.23 |
Paired orbitals |
|
2.Nonbonding molecular orbitals (NBMOs) are MOs with an energy «j ¼ a, xj ¼ 0. The number of NBMOs is at least equal to the absolute value of the difference between the numbers of atoms in the two sets. Thus odd AHs (AHs with an odd number of atoms) have at least one NBMO.
3.NBMOs must be Ôself-pairedÕ, i.e., their coefÞcients must vanish on one set of atoms
(the pairing condition cojm ¼ co jm requires that cojm ¼ 0). Thus an NBMO is conÞned entirely to one set of atoms, the larger one if they differ in size. The coefÞcients on
atoms that are attached to an atom with cjm ¼ 0 must add up to zero.
4.The p-charge densities qm of neutral AHs (Equation 4.9) are unity on all atoms m.
5.The bond orders pmn between all atoms of one set of a neutral AH vanish (Equation 4.24).
XX
|
bj cj*mcj*n ¼ bj cjomcjon ¼ 0 |
j |
j |
|
Equation 4.24 |
Rule 4 enables us to determine the coefÞcients of NBMOs without diagonalizing the H€uckel matrix.287 Start by assigning an arbitrary value of a to one of the atoms with nonvanishing coefÞcients. Then assign multiples or fractions of a to the other atoms in the same set, using rule 3 that the coefÞcients on atoms that are attached to an atom with cNBMO,m ¼ 0 must add up to zero. Finally, the NBMO must be normalized (Equation 4.25), whereby the value of a is deÞned.
X
c2NBMO; ¼ 1 m
m
Equation 4.25
As an example, we show the NBMO of the benzyl radical in Figure 4.19.
Figure 4.19 Back-of-an-envelope determination of the NBMO of benzyl
158 |
Quantum Mechanical Models |
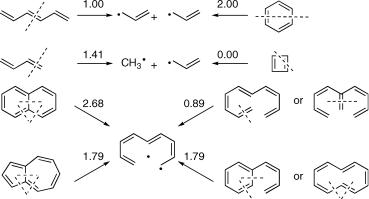
Scheme 4.1 HOMO–LUMO energy gaps in b units determined by PMO theory
Because the p-charge densities qm of neutral AHs (including odd AH radicals such as benzyl) are unity on all atoms Cm (rule 5), the excess charges qm 1 of the benzyl anion and cation obtained by adding or removing an electron to or from the NBMO are equal
to c2NBMO;m , respectively.
The CoulsonÐRushbrooke theorems have many important consequences that will lead us a long way towards a qualitative understanding of the electronic structure of conjugated molecules, particularly of their excited states. Dewar developed a simple perturbation
method (PMO theory) to evaluate the HOMOÐLUMO gap and the associated excitation energy for p-systems with an even number of conjugated atoms.284,285,288 Because the
NBMO of odd AHs can be determined so easily, the system of interest is dissected into two odd AHs. Some examples are shown in Scheme 4.1.
To calculate the HOMOÐLUMO gap of the original system, the coefÞcients of the two fragment NBMOs 1 and 2 are determined. To recombine the NBMOs through the bonds that were cut, we must Þrst choose the symmetry-adapted linear combinations c ¼ (cNBMO,1 cNBMO,2)/H2. The resulting energy changes are then calculated by the formula for Þrst-order perturbation (Equation 4.14). First-order perturbations are additive, so if several bonds connecting atoms r on fragment 1 with atoms s on fragment 2 are formed upon reunion, all energy changes are summed. The resulting HOMOÐLUMO gaps (Equation 4.26) are shown above the corresponding arrows in Scheme 4.1. The HOMOÐLUMO energy gaps are also equal to the total p-energy changes dEp when two
odd AH fragments are united; according PMO theory, dEp is approximately equal to the stabilization of the two electrons in the NBMOs of the fragments.284,285,288
X
«LUMO «HOMO ¼ 2 c1rc2sbrs
r--s
Equation 4.26 HOMO–LUMO energy gaps predicted by PMO theory
There is an ambiguity in using Equation 4.26 because there are several ways to divide AHs into two odd AHs and the resulting HOMOÐLUMO gaps need not be the same. The best Þrstorder estimate will come from the division that minimizes the NBMO splitting. In general, ÔaromaticÕ topologies that strongly stabilize a p-electron system in the ground state feature a large splitting of the NBMOs. Such systems have large excitation energies. Thus PMO theory
The Need for Improvement; SCF, CI and DFT Calculations |
159 |
predicts an approximate mirror-image relationship between the p-electron energies of molecules in the ground state and in the lowest excited state (S1 or T1).289
Perturbation theory is especially well suited to predict the effect of substitution on electronic transitions. The shifts d«j of individual orbital energies upon inductive or resonance perturbation are given in Section 4.3. For a transition that is described by single excitation from a bonding orbital ci to an unoccupied orbital cj, the transition energy is given by «j «i (Equation 4.19), so the band shift calculated by Þrst-order perturbation is easily obtained from Equation 4.27. An example is given in Case Study 4.1.
dD« ¼ d«ðj 1Þ d«ði 1Þ
Equation 4.27 Inductive effect on transition energies
If the transition considered is the HOMOÐLUMO transition of an alternant hydrocarbon, then Þrst-order theory predicts that inductive perturbation will have no effect at all, because d«ðj 1Þ ¼ d«ði 1Þ as a consequence of the pairing theorem. Small red shifts are in fact observed that can be attributed to hyperconjugation with the pseudo-p MO of the saturated alkyl chain.290 On the other hand, alkyl substitution gives rise to large shifts in the absorption spectra of radical ions of alternant hydrocarbons whose charge distribution is equal to the square of the coefÞcients of the MO from which an electron was removed (radical cations) or to which an electron was added (radical anions), and these shifts are accurately predicted by HMO theory.291
4.7 The Need for Improvement; SCF, CI and DFT Calculations
We have started by deleting all interaction terms between the electrons to obtain an
^ |
0 |
, because this allowed us to solve the resulting Schrodinger€ |
ÔapproximateÕ Hamiltonian H |
|
equation easily for Þxed nuclear positions (Figure 1.10). The total neglect of electronic repulsion is clearly a poor approximation, but the resulting electronic wavefunctions can be used to calculate electronic repulsion as an afterthought. In the following, we retain the frozen core approximation, that is, we consider only the p-electrons of conjugated molecules. If H€uckel MOs are taken as a starting point, reintroduction of the interelectronic repulsion terms 1/r12 into the Hamiltonian operator (Section 1.4) results in two types of new contributions to the energy.
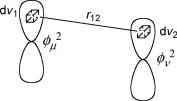
Consider the interaction of two electrons, e1 and e2, that are located in the AOs fm and fv. We do not exclude the possibility that the two electrons are in the same AO, m ¼ v, provided that they have opposite spin. The time-averaged distribution of electron 1 is given by f2uðe1Þdv1 and that of electron 2 by f2v ðe2Þdv2 (Born interpretation). Therefore, the
Figure 4.20 Coulomb repulsion between the electron density in two volume elements

160 |
Quantum Mechanical Models |
Coulomb repulsion between e1 and e2 is obtained by summing all repulsive contributions for electron e1 in a small volume element dv1 and of e2 in dv2 (Figure 4.20).
Integration over all space (dv ¼ dv1dv2 ¼ dx1dy1dz1dx2dy2dz2) yields the Coulomb repulsion integral Jij for two electrons in MOs ci and cj (Equation 4.28).
Jij |
¼ |
*ci2 |
ð |
e1 |
|
1 |
cj2 |
ð |
e2 |
+ * |
|
|
cimfm |
e1 |
Þ |
2 |
|
1 |
|
|
cjnfn |
e2 |
Þ |
2+ |
|
|
m |
|
|
n |
|||||||||||||||||||||
|
|
|
Þ r12 |
|
|
Þ ¼ |
ð |
|
|
r12 |
|
ð |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Equation |
4.28 |
Coulomb repulsion integral |
J |
|
|
|
|
|||||||||||
The integral J can be simpliÞed to the double sum of two-centre Coulombic repulsion integrals gmn (Equation 4.29) by adopting the zero differential overlap (ZDO) approximation, that is, we assume that atomic orbitals located on different atoms do not overlap, fmfn ¼ 0 for m 6¼n.
Jij |
|
|
ci2mcj2ngmn; where gmn |
¼ |
*fm2 |
ð |
e1 |
|
1 |
fn2 |
ð |
e2 |
+ |
m n |
|
||||||||||||
|
|
|
|
Þ r12 |
|
|
Þ |
||||||
|
|
X X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Equation 4.29 |
|
|
|
|
|
|
|
|
||
In semiempirical calculations, gmm 10.8 eV is commonly |
used for |
two electrons |
||
2 |
|
mn |
for m 6¼n |
2 |
occupying a p-orbital on the same carbon atom m and the integrals g |
|
|
are |
|
usually estimated by a point charge approximation, |
gmn e /(rmn þ a), where a ¼ e / |
gmm ¼ 133 pm, that is, gmn 1440/(rmn/pm þ 133) eV. |
|
We are not completely Þnished, however, because we have implicitly assumed that electrons are distinguishable (identiÞable as e1 and e2), which is not possible in fact and therefore not allowed in quantum mechanics. A correct calculation using Slater determinants for electronic conÞgurations (Section 4.1) yields a correction to the Coulomb repulsion Jij for electrons with parallel spin that has no classical analogy, the socalled exchange integral Kij (Equation 4.30), which represents the Coulomb repulsion between the overlap densities cicjdv1 and cicjdv2.h Due to the trafÞc rule arising from the Pauli principle (Fermi hole, Section 1.4), the effective repulsion between electrons of parallel spin, Jij Kij, is less than expected from classical physics. The approximate righthand expression is again obtained with the ZDO approximation.
Kij |
¼ |
*ci |
e1 cj |
e1 |
|
1 |
ci |
e2 |
cj |
e2 |
+ |
cimcjmcincjngmn |
|
|
|||||||||||||
|
ð |
Þ ð |
|
Þ r12 |
|
ð |
|
Þ ð |
|
Þ |
m n |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
X X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Equation 4.30 Exchange integrals
We have started with HMOs that are not eigenfunctions of a Hamiltonian ^ that includes
H
electronic repulsion terms. However, we can now re-optimize the AO coefÞcients of the
^ |
^ HMO |
, that is, by setting |
HMOs by solving the secular equations for the operator H instead of H |
||
the secular determinant equal to zero, ||Hij dij«|| ¼ 0 (Equation 1.16, Section 1.4). The MOs
h It is unfortunate that the reverse assignment of symbols has emerged in EPR spectroscopy, i.e. J for the exchange integral and K for the Coulomb integral. We retain the symbols that are generally used in the context of electronic spectra and are recommended by IUPAC. The integrals are given in atomic units (Table 8.3).

The Need for Improvement; SCF, CI and DFT Calculations |
161 |
so obtained will differ from the HMOs used to calculate the integrals J and K and, conversely, calculation of the latter from the new MOs will give different values for J and K. Hence the
new MOs are still not proper eigenfunctions of ^ and the procedure must be repeated until
H
the MO coefÞcients no longer change substantially. Once the orbitals are reproduced essentially unchanged by further reoptimization, we have reached a self-consistent field (SCF). The mathematical procedure described above is called the HartreeÐFock (HF) procedure. It must be done iteratively, because one needs some trial MOs beforehand to calculate the integrals J and K that, in turn, are needed to optimize the orbitals.
The orbital energies obtained by SCF theory are given by Equation 4.31, where the sum runs over all orbitals that are doubly occupied in the ground conÞguration and the so-called core integrals hii are the energies of a single electron in MO ci in the Þeld of the frozen core of nuclei and the s-electrons (but not the other p-electrons). They correspond to HMO energies.
occ |
|
«i ¼ hii þ Xj |
ð2Jij Kij Þ |
Equation 4.31 SCF orbital energies
Equation 4.31 can be derived on an intuitive basis. Consider the following simple cases. The energy of an electron in a single doubly occupied orbital ci is «i ¼ hii þ Jii, which is the same as hii þ 2Jii Kii obtained from Equation 4.31, because Jii ¼ Kii, as follows from the deÞnitions, Equations 4.29 and 4.30. Noting that that the effective repulsion between electrons of parallel spin amounts to Jij Kij, the energy of an electron in orbital ci in a system containing four electrons in orbitals ci and cj is «i ¼ hii þ Jii þ 2Jij Kij.
Orbital energies are related to oxidation and reduction of molecules. Koopmans theorem states that, on the basis of a single determinant SCF calculation for a closed-shell molecule, the orbital energies deÞned by Equation 4.31 are the best estimate for the vertical ionization energies, Iv,i ¼ «i, of that molecule in the gas phase, which are determined by photoelectron spectroscopy. Similarly, the energies of unoccupied orbitals are a measure of electron afÞnities, Eea ¼ «j, where Eea are the energies required to detach an electron from a singly charged negative ion.i SCF (and also HMO orbital energies) also correlate well with standard potentials for oxidation or reduction determined in solution (Figure 4.1).
The total energy of a given electronic ground conÞguration x0 is given by Equation 4.32. Note that it is not simply twice the sum the energies of the occupied orbitals as in HMO theory, because that would count the interaction between each pair of electrons twice.
occ |
occ |
occ occ |
XX X X
Eðx0Þ ¼ ðhii þ «iÞ ¼ 2 |
hii þ |
ð2Jij KijÞ |
i |
i |
i j |
Equation 4.32 SCF energy of a ground configuration
An excited singlet or a triplet conÞguration can be built by promoting an electron from an occupied orbital ci to a unoccupied orbital cj (Figure 4.1). Their energies above that of the ground conÞguration are given by Equation 4.33, which follows from Equations 4.31 and 4.32.
i The energies of unoccupied (ÔvirtualÕ) orbitals obtained by ab initio calculations are, however, not suitable to estimate electron afÞnities and reduction potentials.
162 Quantum Mechanical Models
Eð1xi ! j Þ Eð1x0Þ ¼ «j «i Jij þ 2Kij
Eð3xi ! j Þ Eð1x0Þ ¼ «j «i Jij
Equation 4.33 Energies of singly excited configurations 1xi ! j and 3xi ! j
Thus, the energy difference between identical singlet and triplet configurations amounts to twice the exchange integral between the orbitals ci and cj that are involved in the excitation (Equation 4.34).
Eð1xi ! j Þ Eð3xi ! j Þ ¼ 2Kij
Equation 4.34 Energy difference between singlet and triplet excited configurations
This is an important result of SCF theory. In fact, we can estimate the size of the integral Kij fairly well using H€uckel MOs, so that we usually do not need to do any SCF calculation at all! Equations 4.33 and 4.34 can again be justiÞed intuitively, if one allows for a stabilizing contribution of Kij for exchangeable electrons of the same spin and a destabilizing one of þ Kij for exchangeable electrons of opposite spin, provided
that their |
exchange is |
allowed by |
the |
Pauli |
principle. For example, the energies |
||||
of 3the |
|
1 |
|
1 |
1 |
are |
1 |
1 |
and |
|
x |
i ! j ¼ ci |
cj |
Eð xi !1 j Þ Eð x0Þ3 ¼ hii þ hjj þ Jij þ Kij |
|||||
|
conÞgurations |
|
|
|
|
|
|
||
Eð xi ! j Þ Eð x0Þ ¼ hii |
þ hjj þ Jij Kij , hence Eð xi ! j Þ Eð xi ! j Þ ¼ 2Kij . |
|
|||||||
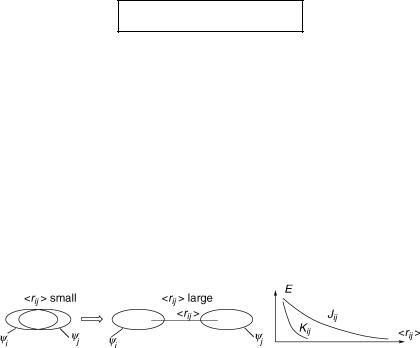
Let us note some important qualitative rules regarding the exchange integrals Kij that determine the energy gap DEST between 1xi ! j and 3xi ! j . The Coulomb integral Jij falls off roughly as 1/<rij>, as the orbitals ci and cj move apart to some ÔaverageÕ distance <rij> (Figure 4.21). The exchange integral representing an overlap repulsion falls of in an exponential manner, exp( <rij>), that is, much more rapidly.
Figure 4.21 Distance dependence of Coulomb integrals Jij and exchange integrals Kij
Thus, for a transition with charge-transfer character (small Kij), the singlet–triplet splitting will be small and the singlet absorption will be at longer wavelengths than expected from the HMO energy gap D«. These conclusions follow immediately from Equations 4.34 and 4.33, respectively. Examples are radical ion pairs or the charge-transfer state in a covalently linked donorÐacceptor molecule such as 4-amino-40-nitrostilbene, and also n,p -excited states of ketones (acetone or benzophenone), where the n-orbital is localized on the oxygen atom and the p -orbital is distributed over a conjugated system and has a small coefÞcient on the oxygen atom. At the other extreme, the HOMOÐLUMO p,p -transitions of alternant hydrocarbons will have a very large singletÐtriplet splitting and lie at relatively short wavelengths, because the HOMO and LUMO coefÞcients at a given atom have the same magnitude (Section 4.6), that is, the HOMO and LUMO are focused on the same atoms and <rij> is small. This also explains the ÔanomalousÕ properties (Figure 4.17) of azulene (1) and cycl[3.3.3]azine (2, Case Study 4.1).
The Need for Improvement; SCF, CI and DFT Calculations |
163 |
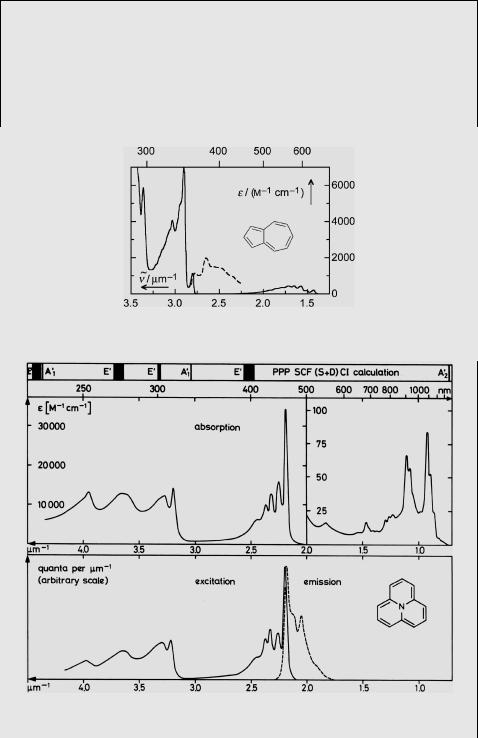
Case Study 4.1: Spectroscopy – electronic spectra and photophysical properties of azulene (1) and cycl[3.3.3]azine (2)
The absorption and ßuorescence spectra of azulene (1) and cycl[3.3.3]azine (2) are shown in Figures 4.22 and 4.23. The ßuorescence emissions are from the second excited singlet state S2, in violation of Kasha s rule (Section 2.1.8), due to the large energy gap between the S1 and S2 states in these compounds.
Figure 4.22 Absorption (adapted from280) and fluorescence (- - -) emission spectra of azulene (1)
Figure 4.23 Absorption, fluorescence emission (- - -) and excitation spectra of cycl[3.3.3] azine (2). Reproduced by permission from ref. 36
164 Quantum Mechanical Models
The Þrst absorption bands of 1 and 2 fall way off the regression line (Figure 4.17), which correlates the p bands of benzenoid hydrocarbons with the corresponding HMO
energy gaps D«: Anthracene |
is |
colourless |
ð |
n~0 0 |
¼ |
1:9 mm 1 |
Þ |
, whereas 1 is blue |
||
ðn~0 0 ¼ 1:0 mm 1Þ, |
292 |
although |
|
|
|
|
||||
|
their HOMOÐLUMO gaps |
are nearly the same |
||||||||
(D« ¼ 0.828b and |
0.877b, |
respectively). |
Tetracene is |
yellow, D« ¼ 0.59b, |
||||||
n~0 0 ¼ 2:1 mm 1, whereas the Þrst band of 2 with D« ¼ 0.63b lies in the near-IR region, ~v0 0 ¼ 0:7 mm 1. Why does H€uckel theory fail to reproduce the twofold (1) and threefold (2) change in energy of the lowest excited singlet state?
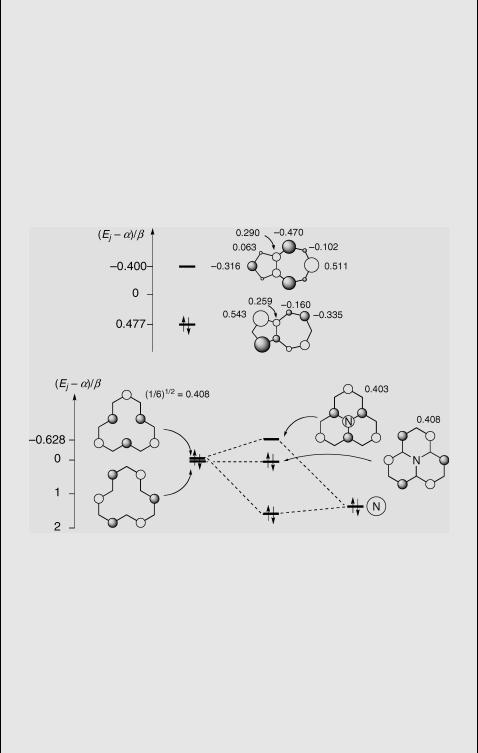
The HMO frontier orbitals of azulene (1) and cycl[3.3.3]azine44,45 (2) are shown in Figure 4.24. For 2 (bottom) they can be constructed simply by considering the interaction of the central nitrogen lone pair with the symmetry-adapted (Section 4.4) NBMOs of [12]annulene. The parameter for the central N atom is daN ¼ 1.5b (Table 8.5; dbC N ¼ 0 is assumed because 1 is planar).
Figure 4.24 HMO frontier orbitals of 1 (top) and 2 (bottom)
The HOMOÐLUMO gap is obtained as 0.63b by a full HMO calculation for 2 (Þrstorder perturbation using only the frontier orbitals gives 0.69b). Inspection of Figure 4.24 reveals that the local overlap between the HOMO and LUMO orbitals of these molecules is very small, that is, the MO coefÞcients are largely (1) or completely (2)
separated to different sets of atoms. Therefore, the exchange integral KHOMO, LUMO is very small, 0.25 eV292 in the case of 1 and essentially zero in the case of 2. In the
alternant hydrocarbons anthracene and tetracene, the HOMO and LUMO coefÞcients are large on the same atoms and the exchange integrals KHOMO, LUMO are large ( 0.7 eV). The ÔanomaliesÕ of 1 and 2 (Figure 4.17) may thus be traced to HMO s total neglect of electronic interaction: From Equation 4.33, one would predict that the energies of their lowest excited singlet states would be lower by 0.9 and 1.4 eVor 0.7 and

The Need for Improvement; SCF, CI and DFT Calculations |
165 |
Figure 4.25 Inductive perturbation of the S0 S1 transition of 2. Reproduced by permission from ref. 34
1.1 mm 1, respectively, than predicted by HMO theory. From Equation 4.34, we expect that these compounds have very small singletÐtriplet energy gaps, in contrast to the
alternant hydrocarbons anthracene and tetracene. Indeed, DEST(1) ¼ 5.4 kJ mol 1,293 and DEST(2) 2 kJ mol 1.34
Cyclazine is isoconjugate to the phenalenyl anion 4 (Figure 4.25). Phenalenyl radical 4. is an alternant hydrocarbon with a charge density of 1 on all carbon atoms. The excess charge in 4 is given by the square of its NBMO, qm ¼ 1/6 ¼ 0.167 on atoms m ¼ 1, 3, and so on. Because HOMOÐLUMO excitation is accompanied by substantial charge reorganization, one expects large shifts of the absorption bands upon substitution. For example, many aza-substituted cyclazines with N atoms in positions 1 and 3 are known. Using Þrst-order perturbation theory (Equation 4.13), one predicts that each N atom will stabilize the HOMO by 0.4082 daN ¼ 0.25b. The LUMO will not be affected, because c1,LUMO ¼ c3,LUMO ¼ 0. Indeed the position of the Þrst absorption band of azacyclazines correlates well with the number of N atoms. It is shifted all the way from the near-IR region in parent 2ðn~0 0 ¼ 0:7 mm 1Þ throughout the visible region up to ðn~0 0 ¼ 2:4 mm 1Þ in 1,3,5,7,9,11-hexaazacycl[3.3.3]azine.34
SCF calculations provide improved MOs, because the average electronic repulsion is minimized, but the correlation of electronic movements is still neglected. Ab initio SCF calculations using the HF procedure do not adopt the ZDO and frozen core approximations mentioned above. Nevertheless, the energies calculated by ab initio methods for singledeterminant wavefunctions are still much too high, even if an ÔinÞnitelyÕ large basis set of AOs, referred to as the Hartree–Fock limit, is used to optimize the molecular orbitals. The excess relative to the true energy is called the correlation error and amounts to roughly 1 eV per electron pair. Although we have accounted for electronic repulsion by calculating the best orbitals for a single electron in an averaged Þeld of all the other electrons and nuclei, we have not considered their movements explicitly, having retained the notion of MOs that describe the motion of a single electron. SCF wavefunctions are still essentially
