
- •Оглавление Баскаков с.И. Радиотехнические цепи и сигналы. Руководство к решению задач, 2002
- •Раздел I включает шестнадцать отдельных тем, которые охватывают всю программу курса. Тематические заголовки повторяют названия глав учебника [1].
- •Раздел II пособия содержит указания к решению ряда задач. В разделе III приведены образцы решений. Последний раздел IV включает в себя ответы к задачам.
- •Раздел I
- •Тема 2спектральные представления сигналов
- •Тема 4 модулированные сигналы
- •Тема 5 сигналы с ограниченным спектром
- •Тема 6 основы теории случайных сигналов
- •Тема 7 корреляционная теория случайных процессов
- •Тема 8 воздействие детерминированных сигналов на линейные стационарные системы
- •Тема 9 воздействие детерминированных сигналов на частотно-избирательные системы
- •Тема 10 воздействие случайных сигналов на линейные стационарные цепи
- •Тема 11 преобразования сигналов в нелинейных радиотехнических цепях
- •Тема 12 преобразование сигналов в линейных параметрических цепях
- •Тема 13 основы теории синтеза линейных радиотехнических цепей
- •Тема 14 активные цепи с обратной связью и автоколебательные системы
- •Тема 15 дискретные сигналы. Принципы цифровой фильтрации
- •Тема 16
- •Раздел II
- •Тема 10
- •Тема 11
- •Тема 12
- •Тема 13
- •Тема 14
- •Тема 15
- •Раздел III
- •Тема 10
- •Тема 11
- •Тема 12
- •Тема 13
- •Тема 14
- •Тема 15
- •Тема 16
- •Раздел IV
- •Тема 10
- •Тема 11
- •Тема 12
- •Тема 13
- •Тема 14
- •Тема 15
- •Тема 16
Тема 6 основы теории случайных сигналов
• Случайные события и их вероятности
6.1(УР). Два лица, А и В, по очереди бросают игральную кость. Игру начинает А. Выигрывает тот, кто первым выбросит шесть очков. Найдите вероятностьРАтого, что выиграет лицо А.
6.2(УО).Некоторый цифровой сигнал представлен кодовыми комбинациями - шестиразрядными двоичными числами, которые образованы случайными комбинациями нулей и единиц. Вероятность появления символа "1" в каждом разряде составляет величинуP1= 0.6, а вероятность символа "О" составляет величинуР0= 0.4. Найдите вероятностьР возникновения конкретной кодовой комбинации 101101, считая появления того или иного символа в каждом разряде независимыми случайными событиями.
6.3(УО). В четырехразрядном цифровом сигнале (см. условия задачи 6.2) появление нуля или единицы в первом разряде равновероятно; в следующих разрядах перемена символа по сравнению с предыдущим значением имеет вероятность 0.8, а сохранение символа имеет вероятность 0.2. Найдите вероятностьР того, что будет реализована кодовая комбинация ОНО.
6.4(УО). Изучение большой партии радиоэлектронных изделий показало, что из 10000 изделий в течение 4 лет исправно работают 8200 экземпляров, а по прошествии 7 лет число исправно работающих изделий составляет 3800. Определите вероятность того, что случайно взятое изделие из числа проработавших 4 года окажется также работоспособным через 7 лет.
6.5(УО). Некоторая система, предназначенная для передачи сигналов из точкиа в точкуb, изображена на рис. I.6.1. Система содержит элементы1 и2, резервирующие друг друга. Нормальное функционирование обеспечивается, если исправен хотя бы один из этих элементов.
Известно, что в течение некоторого промежутка времени элемент 1 исправен с вероятностьюP1= 0.8, а элемент2 - с вероятностьюР2= 0.7. Найдите вероятность Р исправной работы резервированной системы за тот же промежуток времени.
6.6(УО). На входы сумматора (рис. I.6.2) поступают четыре независимых постоянных во времени случайных напряженияu1,u2,u3иu4. Каждое из этих напряжений с равной вероятностью принимает либо значение 0.5 В ("низкий" уровень потенциала),
34
|
|
|
либо 4.5 В ("высокий" уровень потенциала). Определите всю совокупность напряжений uвыхна выходе сумматора вместе с вероятностями их появления.
• Функция распределения и плотность вероятности. Моменты
6.7(О).Постройте график функции распределенияF(uвых) для случайной величиныuвых, рассмотренной в задаче 6.6. Выведите аналитическое выражение плотности вероятностир(uвых).
6.8(Р).Случайная величинаX имеет плотность вероятности
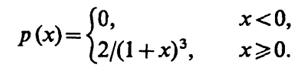
Найдите функцию распределения F(x) данной случайной величины, а также вероятностьР(0 ≤ Х ≤ 1) попадания случайной точки внутрь отрезка [0, 1].
6.9(УО).Случайная величинаX может принимать лишь два значения:х= 1 с вероятностью 0.25 их= 1.5 с вероятностью 0.75. Аналогично, случайная величинаY, независимая отX, может принимать лишь два значения:у= 3 иу= 5 с одинаковыми вероятностями 0.5. Найдите плотность вероятности случайной величиныZ = X + Y.
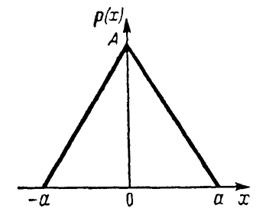
6.10(О).Непрерывная случайная величинаX имеет график плотности вероятностиp(х) треугольного вида (рис. I.6.3). Параметра - заданное число, величинаА заранее неизвестна. Получите формулу, описывающую функциюр(х).
6.11(Р).Случайная величинаX распределена по нормальному закону с параметрамит= 0, σ = 2. Найдите вероятность попадания этой случайной величины в полу отрезок 0 <х≤ 2.
6.12(О).Вычислите вероятность того, что случайная величинаX, рассмотренная в задаче 6.10, попадает в полуотрезок 0 <x≤a/2.
35
6.13(Р).Найдите плотность вероятности случайной величиныR - сопротивления параллельного соединения двух резисторов, один из которых имеет фиксированное сопротивлениеR0, в то время как сопротивление другого резистораr - случайная величина, равномерно распределенная на отрезке [R0-a,R0+a], гдеa<R0- постоянное число.
6.14(Р).Независимые случайные величиныX иY имеют заданные плотности вероятностир1(х) иР2(у) соответственно. Найдите плотность вероятностир3(z) случайной величиныZ = X + Y.
Рис. I.6.3.
6.15(УО).ПустьX иY - две независимые случайные величины, равномерно распределенные на отрезке [0, 1]. Найдите аналитическое выражение функциир(z) - плотности вероятности суммыZ = X + Y этих двух величин.
6.16(О).Вычислите плотность вероятностиpz(z) случайной величиныZ, каждая реализация которой представляет собой сумму реализаций независимых случайных величинXиYс одинаковыми плотностями вероятности экспоненциального вида:рх(х) = λе-λxσ(х),рy(y) = λе-λyσ(y).
6.17(У).Докажите, что случайная величинаX, имеющая распределение Коши с плотностью вероятности
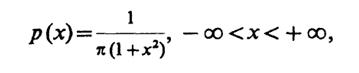
характеризуется бесконечно большой дисперсией.
6.18(О).Вычислите математическое ожиданиеmвыхи дисперсию σ2выхслучайного напряжения на выходе сумматора, рассмотренного в задаче 6.6.
6.19(Р).Вычислите среднее значениех и средний квадратх2случайной величиныX, рассмотренной в задаче 6.8.
6.20(О).Случайная величинаU принимает значения 0.5, 0.8 и 1.3 с вероятностью 0.35, 0.45 и 0.2 соответственно. Вычислите величиныmuи σ2u.
6.21(Р).Непрерывная случайная величинаX равномерно распределена на полуотрезкеа < х ≤ b. Вычислите среднее значениеm2=x, средний квадратт2=х2и дисперсию σ2x=т2-т21данной случайной величины.
6.22 (УО).Случайная величинаX имеет одностороннюю экспоненциальную плотность вероятности
36
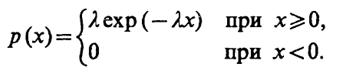
Найдите среднее значение х и дисперсию σ2xэтой случайной величины.
6.23(У).Докажите, что еслиX иY - независимые гауссовы случайные величины с математическими ожиданиямитхитуи дисперсиями σ2xи σ2yсоответственно, то случайная величинаZ = aX + bY, гдеаиb- константы, также обладает свойством нормальности, имея математическое ожиданиеmz = amx + bmyи дисперсию σ2x=а2σ2x+b2σ2y.
6.24(Р).Случайная величинаX равномерно распределена на отрезке [0, 1]. Найдите математическое ожидание и дисперсию случайной величины Z, каждая реализация которой равна произведению длин отрезков, разделенных случайной точкойх.
• Функциональные преобразования случайных величин. Многомерные случайные величины
6.25(Р).Найдите плотность вероятности случайной величиныZ, рассмотренной в задаче 6.24.
6.26(О).Исходная случайная величинаX имеет плотность вероятности экспоненциального вида

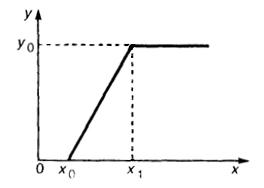
с фиксированным значением параметра λ>0. Случайная величина Y получается изX путем функционального преобразования, график которого изображен на рис. I.6.4. Определите плотность вероятностирпр(у) преобразованной случайной величины.
6.27(УО).Случайная величинаX равномерно распределена на отрезке [0, π/2]. Найдите среднее значение и дисперсию случайной величиныY, реализации которой связаны с реализациями случайной величиныXследующим образом:y= 5 cosx+ 12 cos2x.
6.28(О).Случайная величинаX равномерно распределена на отрезке [a, b]. Получите выражение, описывающее плотность вероятностир(у) случайной величиныY=X2. Найдите математическое ожиданиету и дисперсию σ2y.
6.29(Р).Три независимые случайные величиныX, Y иZимеют одинаковые нормальные плотности вероятности
37
Рис. I.6.4
p(ξ) = ехр (-ξ2/(2σ2)/(√2πσ), где ξ - символ, соответствующийх, у иz. Пусть (x, y, z) - три декартовы координаты точки в трехмерном пространстве, связанные со сферическими координатами (r, υ, φ) известными соотношениями:
x = r sin υ cos φ, y = r sin υ sin φ, z = r cos υ.
Найдите одномерную плотность вероятности р(r) случайной величиныR, представляющей собой длину радиуса-вектора в сферической системе координат.
• Характеристическая функция случайной величины
6.30(О).Найдите характеристическую функцию случайной величиныX, имеющей плотность вероятностирх(х) = λ ехр × (-λх)σ(x).
631(О).Вычислите характеристическую функцию Θ(u) случайной величиныX, равномерно распределенной на отрезкеа ≤ х ≤ b.
6.32(Р).Используя результат, полученный в задаче 6.31, найдите среднее значениех рассмотренной здесь случайной величины.
6.33(Р).Случайная величинаX равномерно распределена на отрезке -1/2 <x< 1/2. Вычислите плотность вероятности случайной величиныY, каждая реализация которой равна сумме трех независимых реализаций случайной величиныX.
6.34(О).Определите вероятность того, что модуль случайной величиныY, рассмотренной в задаче 6.33, принимает значения, превышающие единицу.
6.35(УР).Случайная величинаX имеет гауссову плотность вероятности с известным математическим ожиданиемтх и заданной дисперсией σ2x. Вычислите среднее значение случайной величиныY, отдельные реализации которой связаны с реализациями случайной величиныX соотношениему= ехр(х).
38
Содержание

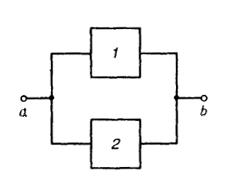 Рис.
I.6.1
Рис.
I.6.1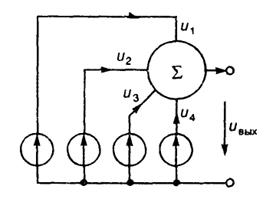 Рис.
I.6.2
Рис.
I.6.2