
- •Оглавление Баскаков с.И. Радиотехнические цепи и сигналы. Руководство к решению задач, 2002
- •Раздел I включает шестнадцать отдельных тем, которые охватывают всю программу курса. Тематические заголовки повторяют названия глав учебника [1].
- •Раздел II пособия содержит указания к решению ряда задач. В разделе III приведены образцы решений. Последний раздел IV включает в себя ответы к задачам.
- •Раздел I
- •Тема 2спектральные представления сигналов
- •Тема 4 модулированные сигналы
- •Тема 5 сигналы с ограниченным спектром
- •Тема 6 основы теории случайных сигналов
- •Тема 7 корреляционная теория случайных процессов
- •Тема 8 воздействие детерминированных сигналов на линейные стационарные системы
- •Тема 9 воздействие детерминированных сигналов на частотно-избирательные системы
- •Тема 10 воздействие случайных сигналов на линейные стационарные цепи
- •Тема 11 преобразования сигналов в нелинейных радиотехнических цепях
- •Тема 12 преобразование сигналов в линейных параметрических цепях
- •Тема 13 основы теории синтеза линейных радиотехнических цепей
- •Тема 14 активные цепи с обратной связью и автоколебательные системы
- •Тема 15 дискретные сигналы. Принципы цифровой фильтрации
- •Тема 16
- •Раздел II
- •Тема 10
- •Тема 11
- •Тема 12
- •Тема 13
- •Тема 14
- •Тема 15
- •Раздел III
- •Тема 10
- •Тема 11
- •Тема 12
- •Тема 13
- •Тема 14
- •Тема 15
- •Тема 16
- •Раздел IV
- •Тема 10
- •Тема 11
- •Тема 12
- •Тема 13
- •Тема 14
- •Тема 15
- •Тема 16
Раздел I включает шестнадцать отдельных тем, которые охватывают всю программу курса. Тематические заголовки повторяют названия глав учебника [1].
Подбор задач и их расстановка выполнена таким образом, что учащимся предлагается внутренне организованная система упражнений, отвечающая общим и частным принципам построения курса "Радиотехнические цепи и сигналы". Так, читатель найдет здесь задачи, преследующие цель закрепить теоретический материал. Имеются задачи следующей ступени сложности, когда приемы и методы познавательной деятельности должны быть обобщены учащимся для анализа более сложных ситуаций. Наконец, в пособие включены задачи, предусматривающие перенос знаний на новые объекты, выработку навыков творческого мышления.
Раздел II пособия содержит указания к решению ряда задач. В разделе III приведены образцы решений. Последний раздел IV включает в себя ответы к задачам.
Автор стремился написать пособие, которое активно помогало бы студенту в наиболее сложной фазе работы - в поиске плана решения задач. Для этого была проведена классификация всех помещенных в книге задач. Классификационные символы располагаются в скобках вслед за номером задачи и имеют следующий смысл:
УР- к задаче приведены указания (для хорошо подготовленных студентов, намеренных решить задачу "без подсказки") и решение;
Р- приведено только решение;
УО- данную задачу сопровождают указания и ответ;
У- приводится только указание;
О- приводится только ответ.
Изучение каждой темы следует начинать с проработки установочных задач типов УР и Р. При выполнении упражнений студенту целесообразно иметь под рукой учебник по теории цепей, например, [2] и математические справочники, такие, как [3] и [4].
5
Содержание
Раздел I
Задачи и упражнения
Тема 1
ОБЩАЯ ТЕОРИЯ РАДИОТЕХНИЧЕСКИХ СИГНАЛОВ
• Математические модели сигналов
1.1(Р). Импульсный сигналu(t), имеющий размерность напряжения (В), описывается формулой
u(t) = 25[ехр(-105t- ехр(-2 · 105t)] σ(t).
Постройте график данного импульса. Определите максимальное значение сигнала umax, а также момент времени достижения максимумаtmax. Вычислите длительность импульса τи, определив ее как длину отрезка времени от нуля до той точки, в которой мгновенное значение сигнала уменьшается в 10 раз по сравнению с максимальным значением.
1.2(О). Математическая модель импульсного сигнала задана выражением
u(t) =A0te-αt.
Вычислите и постройте график данного сигнала в зависимости от безразмерного аргумента αt. Определите длительность импульса τи, приняв в качестве критерия окончания импульса спад мгновенных значений до уровня 0.1 от максимального значения.
1.3(УО).Осциллограмма сигналаs(t) приведена на рис. I.1.1. Запишите математическую модель данного сигнала, применив функции Хевисайда.
1.4(Р).Сигналs(t) имеет математическую модель вида (рис. I.1.2):
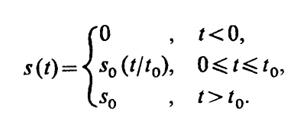
Представьте данную зависимость в виде суммы кусочно-линейных функций.
6
|
|
|
1.5(O).На рис. I.1.3,а, б, в изображены осциллограммы импульсных сигналовs1(t),s2(t) иs3(t). Найдите математические модели данных сигналов, выраженные посредством сумм, которые составлены из произведений линейных функций и функций Хевисайда.
1.6(О).Найдите формулы, описывающие математические модели следующих импульсных сигналов (рис. I.1.4): а) однополярного импульсаs1(t), представляющего собой отрезок синусоиды с амплитудойА и частотой ω0; длительность импульса равна половине периода (а); б) двухполярного импульсаs2(t), отвечающего целому периоду синусоиды с такими же параметрами (б).
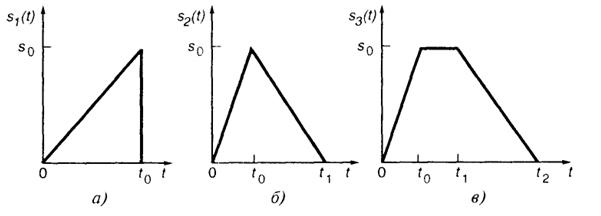 Рис.
I.1.3
Рис.
I.1.3
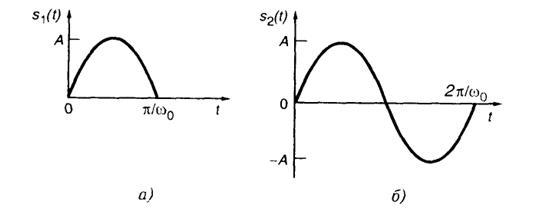 Рис.
I.1.4
Рис.
I.1.4
7
1.7(О).Математическая модель сигнала задана некоторой функциейf(t), существующей в бесконечном промежутке времени -∞<t<∞. Представьте функциюf(t) в виде суммы четной и нечетной частей:
f(t) =fчт(t) +fнч(t)
и найдите явные выражения для функций fчт(t) иfнч(t).
• Динамическое представление сигналов
1.8(О).Используя функции Хевисайда, найдите динамическое представление колебанияs(t), описывающего переход некоторой физической системы от нулевого уровня к постоянному уровнюВ. Данный переход происходит за интервал времениТ по линейному закону:
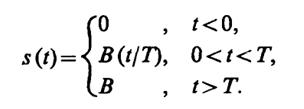
1.9(O).Экспоненциальный видеоимпульс напряжения (В)s(t) = 25ехр(- 106t)σ(t) действует на входе цепи, достаточно инерционной для того, чтобы можно было приближенно представить данный сигнал в видеs(t) =Aδ(t). Определите числовое значение коэффициентаА.
1.10(Р).Убедитесь, что приn→∞ пределом последовательности функций
fn(t) = (n/2)е-n|t|
служит функция Дирака δ(t).
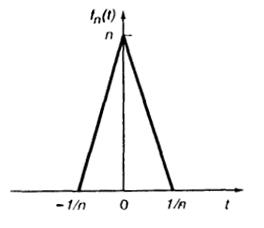
1.11(Р). Докажите, что пределом последовательности функцийfn(t), одна из которых изображена на рис. I.1.5, приn→∞ является функция δ(t).
1.12(У).Докажите, что функция Дирака δ(t) может рассматриваться как предел последовательности классических функций
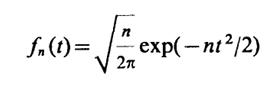
при n→∞. Рис.I.1.5
8
•Геометрические методы в теории сигналов
1.13(Р).Вычислите энергиюЕи и норму ||u|| экспоненциального видеоимпульса напряжения (В)
u= (t) = 30ехр(-105t)σ(t).
1.14(О).Вычислите энергиюЕs и норму ||s|| сигналаs(t), представляющего собой прямоугольный видеоимпульс напряжения (В) с амплитудойU0и длительностью τи.
1.15(О).Выведите формулу для нахождения энергии радиоимпульса длительностью τис огибающей прямоугольной формы, описываемого выражением
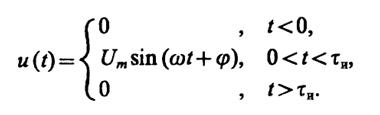
1.16(Р).Даны два сигнала: прямоугольный видеоимпульсu(t) =U0[σ(t) - σ (t- τи)] и экспоненциальный видеоимпульсv(t) =U0eαtσ(t) (параметрыU0, α и τи- положительные вещественные числа). Считая длительность τификсированной, найдите величину параметра ос, при которой расстояниер(u, v) минимально.
1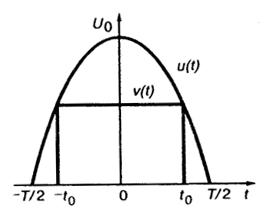 .17(Р).Сигналf(t) =t2существует на отрезке времени 0 ≤t≤ 1. Найдите приближение к этому сигналу
с помощью линейной функцииu(t)
=At+B, наилучшее в смысле
минимума расстояния (метрики).
.17(Р).Сигналf(t) =t2существует на отрезке времени 0 ≤t≤ 1. Найдите приближение к этому сигналу
с помощью линейной функцииu(t)
=At+B, наилучшее в смысле
минимума расстояния (метрики).
1.18(О).На отрезке времени -Т/2 ≤t≤Т/2 задан импульсный сигналu(t) =U0cos(πt/T), тождественно обращающийся в нуль вне указанного отрезка (рис. I.1.6). Сигналv (t) представляет собой прямоугольный импульс длительностью 2t0, вписанный в импульсu(t). Определите параметрt0таким образом, чтобы расстояниер(и, v) было минимальным.
Рис. I.1.6
• Теория ортогональных сигналов
1.19(Р).Пусть {un(t)},n= 1, 2, 3, ... - система ортогональных сигналов, существующих на общем отрезкеa≤t≤b и являющихся векторами некоторого гильбертова пространства. Докажите, что эта система сигналов линейно независима.
9
1.20(Р).Докажите, что конечная система сигналови1(t),u2(t),...,иN(t), заданная на отрезке времениa≤t≤b, является линейно зависимой в том случае, когда обращается в нуль определитель Грамма:
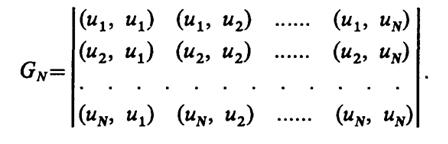
1.21(O).Сигналыu(t) иv(t) представляют собой прямоугольные видеоимпульсы с амплитудамиА1иА2и длительностями τи1и τи2соответственно (рис. I.1.7). Оба сигнала одновременно отличны от нуля на отрезке времени длительностью τ. Докажите, что уголψ между этими сигналами, рассматриваемыми как векторы в гильбертовом пространстве, не зависит от вели
|
|
|
чин А1иА2. Получите формулу, определяющую уголψ.
1.22(О).Два одинаковых по форме экспоненциальных видеоимпульса, разнесенных во времени на величинуt0, описываются выражениями
u1(t) =U0е-αtσ(t),u2(t) =U0е-α(t-t0)σ(t-t0).
Определите зависимость угла ψ между этими векторами от параметраt0. Найдите величинуt0, при которой ψ = 89° (практически ортогональные импульсы).
1.23(У).В гильбертовом пространстве сигналов заданы два вектораuиv с одинаковыми энергиями: ||u||2= ||v||2. Докажите, что при этом сигналыs1=u + vиs2=u - vортогональны, т.е. (s1,s2) = 0.
1.24(У).Для произвольных сигналовu(t) иv(t), являющихся элементами гильбертова пространства, докажите равенство параллелограмма
||u + v||2+||u - v||2= 2|u|2+ 2|v|2.
1.25(Р).Сигналыu(t) иv(t) являются элементами некоторого вещественного гильбертова пространства. Рассматриваемые сигналы линейно независимы, т.е. равенствоu=λvне имеет место ни при каком значении вещественного параметраλ. Докажите справедливость неравенства Коши – Буняковского |(u, v)| < ||u|| · ||v||.
10
1.26(У).Докажите, что в вещественном гильбертовом пространстве сигналов имеет место неравенство Минковского |(u + v)| ≤ ||u|| + ||v||.
1.27(У).В гильбертовом пространстве сигналов заданы произвольный вектори и векторv, такой, что ||v|| = l. По аналогии с геометрией обычных векторов на плоскости векторw= (u, v)vназывают ортогональной проекцией вектораuна направлениеv (рис. I.1.8). Докажите, что вектору = и - w ортогонален векторуv.
1.28(У).Обобщая результат задачи 1.27, докажите, что если {v1,v2, ...,vN}- система взаимно ортогональных векторов с единичными нормами, то вектор
у = и- (и, v1)v1- (u, v2)v2- ... - (u, vn)vn
при любом и ортогонален по отношению к каждому из векторов рассматриваемой системы.
1.29(Р).Пусть в гильбертовом пространстве сигналов задана система взаимно неортогональных векторов {g0,g1...,gn, ...}. Постройте на ее основе ортонормированную систему (u0,u1, ...,иn, ...} таким образом, чтобы каждый вектор uk являлся линейной комбинацией вида
uk=ck0g0+ck1g1+ ... +ckngn+ ...
с постоянными коэффициентами.
1.30(УО).Используя прием, найденный при решении задачи 1.29, вычислите три первых базисных вектораu0,и1ии2, получаемых путем ортогонализации и нормировки системы степенных функций (1,t, t2, ...} на отрезке -l ≤t≤ l.
11
1.31(УО).Найдите первые три коэффициентас0,с1ис2обобщенного ряда Фурье, получаемого при разложении сигналаf(t) = еtна отрезке -1 ≤t≤ 1 по системе базисных функций {uk}, исследованных в задаче 1.30.
Вычислите норму
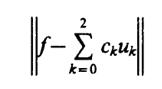
абсолютной ошибки аппроксимации данного сигнала тремя членами ряда. Получите числовую оценку для относительной ошибки

данной аппроксимации.
1.32(УО).Решите предыдущую задачу в другой постановке: найдите коэффициенты многочлена второй степениz(t) =A + Bt + Ct2таким образом, чтобы данный многочлен с наименьшей среднеквадратичной ошибкой аппроксимировал сигналf(t) = еtна отрезке -1 ≤t≤ 1.
133(У).Докажите, что комплексные экспоненциальные функции

на отрезке -T/2 ≤t≤T/2 образуют ортонормированный базис.
1.34(У).На отрезкеa ≤ t ≤ b задана бесконечная полная система ортонормированных сигналов {un(t)},n= 0, 1, 2, ... Докажите, что дельта-функция, сосредоточенная в некоторой внутренней точкеt0(a<t0<b), может быть представлена как бесконечный ряд
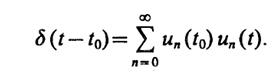
1.35(О). Сигналs(υ), зависящий от безразмерного аргументаυ, на отрезке -1/2 ≤υ≤ 1/2 представляется формулойs(υ) = 16υ2. Вычислите коэффициентс2разложения данного сигнала в обобщенный ряд Фурье по функциям Уолша:
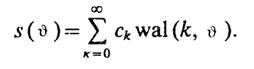
12
1.36(О).Вычислите коэффициентыс0ис2в разложении сигналаs(υ) = 45 ехр (- 0,7 |υ|), заданного на отрезке -1/2 ≤υ≤ 1/2, в обобщенный ряд Фурье по функциям Уолша.
1.37(УО).Найдите коэффициентс1обобщенного ряда Фурье по функциям Уолша для сигналаf(t), рассмотренного в задаче 1.31.
13
Содержание

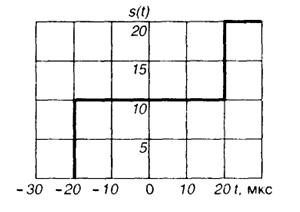 Рис.
I.1.1
Рис.
I.1.1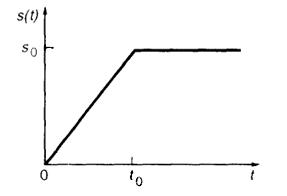 Рис.
I.1.2
Рис.
I.1.2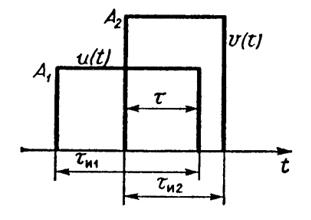 Рис.
I.1.7
Рис.
I.1.7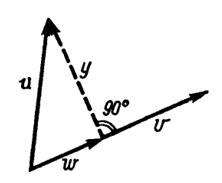 Рис.
I.1.8
Рис.
I.1.8