Статы Экзамен / Статы / statukr

– одночастинкова статсума. Вона дорівнює:

Із формул (4.51), (4.57) і (4.58) одержуємо намагніченість газу:

– функція Бріллюена.

У слабкому магнітному полі g B JH kT з (4.59) і (4.60) випливає:

Закон Кюрі, як і раніше, виконується, однак постійна Кюрі відрізняється від (4.56).

Якщо J і g B J , функція Бріллюена (4.60)

збігається з функцією Ланжевена (4.53), а намагніченість

(4.59) стає рівною (4.52).

В окремому випадку L 0, S J 12 із (4.59) і (4.60)

одержуємо:

B12 x thx ,

140

Звідси видно, що в слабкому полі

2n

M B H , kT

а постійна Кюрі в 3 рази перевищує значення (4.56), отримане без урахування просторового квантування.

4.5. Дворівнева система

Ентропія дворівневої системи була обчислена в підрозділі 1.9 для мікроканонічного ансамблю. Обчислимо її та інші термодинамічні функції цієї системи, використовуючи канонічний розподіл Гіббса.

Припустимо, що рівні енергії частинки 1 , 2 не виро-

джені. Тоді статсума системи, зумовлена внутрішнім ступенем свободи частинок, дорівнює:

Вільна енергія, ентропія і внутрішня енергія дворівневої системи дорівнюють:

141

Асимптотики внутрішньої енергії (4.65) дорівнюють:

N , kT , E ДС N 1 , kT .

0

При низьких температурах майже всі частинки перебувають на нижньому рівні 1 , а при високих – рівномірно

заповнюють рівні.

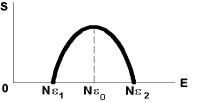
Ентропія (4.64) виражена через число частинок у системі і її температуру. На рис. 4.4 приведений графік залежності ентропії від енергії дворівневої системи.

Рис. 4.4. Ентропія дворівневої системи

Ця залежність отримана шляхом виключення T з формули (4.64) за допомогою співвідношення (4.65). Видно, що в цілком упорядкованому стані, коли всі частинки перебувають на нижньому рівні або на верхньому, ентропія дорівнює нулю. Енергія N 0 відповідає цілком невпорядкова-

ному стану з максимальною ентропією. На висхідній гілці

142

кривої S E температура позитивна, а на низхідній – нега-

тивна. Негативній температурі відповідає інверсна заселеність рівнів 1 , 2 .

Диференціюючи (4.65) за температурою, одержуємо теплоємність дворівневої системи:

Рис. 4.5. Крива Шотткі

Асимптотики теплоємності (4.66) мають вигляд:

Як і в підрозділі 4.3, наявність щілини в енергетичному спектрі системи приводить до експоненціального зменшення її теплоємності при наближенні температури до абсолютного нуля.

143

РОЗДІЛ 5. ІДЕАЛЬНІ ФЕРМІ- І БОЗЕ-ГАЗИ

5.1.Розподіл Фермі – Дірака

Уцьому підрозділі ми одержимо функцію розподілу для ідеального газу ферміонів – частинок з напівцілим спіном. Вважається, що в гамільтоніані системи відсутня міжчастинкова взаємодія. Однак частинки підкоряються принципу

Паулі. Їх число ni у стані i дорівнює нулю або одиниці: ni 0, 1. Тут i – індекс одночастинкового стану. У випадку вільного фермі-газу в ролі i зручно взяти набір i p, , де p – імпульс частинки, а – спінове квантове число.

Позначимо через ni середнє число частинок у стані i .

Щоб знайти його, застосуємо до частинок у цьому стані великий канонічний розподіл Гіббса. Він стосується відкритої системи, яка обмінюється з термостатом енергією і частинками. Такою системою можна вважати частинки, які перебувають у i -му стані. Як і в підрозділі 3.3, силова взаємодія між цими частинками та іншими відсутня, а квантова обмінна взаємодія існує лише між частинками в одному стані. Енергія цих частинок дорівнює ini , де i – енер-

гія однієї частинки в стані i . Із (3.28) і (3.35) випливає, що великий потенціал цих частинок дорівнює:

Отже, великий потенціал ідеального фермі-газу дорівнює:

144

Середнє число частинок у стані i знаходимо за допомогою формули (2.93):

e kT 1

Ця функція називається функцією розподілу Фермі–Дірака. Її графік наведено на рис. 5.1.

Рис. 5.1. Функція розподілу Фермі – Дірака

Якщо воно фіксоване, рівняння (5.3) може бути використане для обчислення хімічного потенціалу як функції

густини n N V і температури газу. У граничному випадку

розподіл (5.2) перетворюється на больцманівський розподіл

145

(4.26). Підставляючи в нерівність (5.4) вираз (4.22) для хімічного потенціалу газу, одержуємо

де m – маса електрона. Величина в лівій частині цієї нерівності називається тепловою довжиною хвилі де Бройля частинки. Якщо вона мала в порівнянні з середньою

відстанню між частинками V N 13 , квантовими ефектами

можна знехтувати, а для розрахунку термодинамічних величин використовувати розподіл (4.26).

5.2. Вироджений електронний газ

Розглянемо ідеальний електронний газ в об’ємі V . Із квантової механіки відомо, що імпульс, енергія та інші характеристики стану частинки в обмеженому об’ємі квантовані. Тоді підсумовування за i у формулах (5.1) і (5.3) означає підсумовування за дискретними квантовими числа-

ним, а суми за p перетворюються на інтеграли. Для переходу від підсумовування за p до інтегрування можна скористатися правилом (1.18):

Воно означає, що поступальний рух частинок описується квазікласично. Мікростан частинки зіставляється з комір-

146

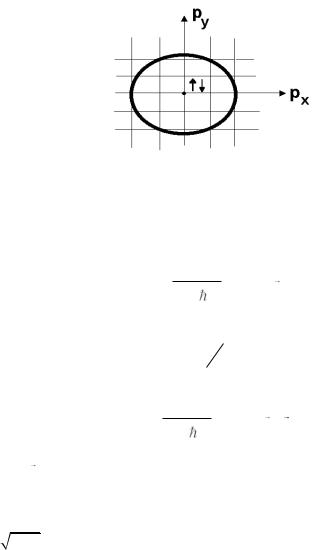
схематично показані комірки в двовимірному імпульсному просторі.

Рис. 5.2. Фазовий простір частинки

За допомогою (5.2) і умови нормування (4.7), з огляду на правило (5.6), знаходимо повне число електронів в системі:

N 2 V 3 d 3 p np . (5.7)

2

Нагадаємо, що спін s частинки має g 2s 1 орієнтацій у просторі. Для електрона s 12 , g 2 .

Внутрішня енергія електронного газу дорівнює:

E 2 V 3 d 3 p p np , (5.8)

2

де p – закон дисперсії частинки (1.2). Переписуючи його у вигляді px2 p2y pz2 2m , бачимо, що поверхнями постійної енергії в імпульсному просторі є сфери радіуса

2m .

Стан електронного газу при нульовій температурі називається основним станом, а електронний газ – цілком виро-

147

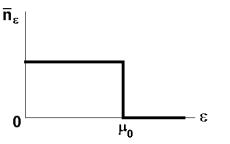
дженим. Із (5.2) видно, що при T 0 розподіл Фермі – Дірака, показаний на рис. 5.1, переходить у «сходинку» Фермі (рис. 5.3).

Рис. 5.3. «Сходинка» Фермі

Тут 0 – хімічний потенціал електронів при нульовій температурі. Він називається енергією Фермі: 0 F . Такий

розподіл означає, що при T 0 усі комірки на рис. 5.2 усередині сфери деякого радіуса pF заповнені, а комірки поза

цією сферою – вільні. Заповнення комірок відбувається так, щоб енергія системи була мінімальною і щоб виконувався принцип Паулі. Тому в кожній комірці містяться два електрони з протилежними спінами. Сфера, яка розмежовує заповнені і порожні комірки, називається сферою Фермі, а її радіус pF – імпульсом Фермі. Енергія Фермі дорівнює:

Імпульс Фермі пов'язаний з густиною електронів. Щоб знайти цей зв'язок, запишемо повне число електронів в об’ємі V . Воно дорівнює подвоєному числу комірок під сферою Фермі:

148

У формулах (5.7) і (5.8) імпульс входить у підінтегральну функцію тільки через енергію. Це дозволяє елементом об’є- му в імпульсному просторі вважати об’єм кульового шару:

d 3 p 4 p2dp . Тоді, використовуючи (1.2), одержуємо:

інтегрування у формулах (5.12) виконується у проміжку

Підставляючи сюди (5.11) і використовуючи формулу (2.7), одержуємо тиск електронного газу при нульовій температурі:

149