Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4603 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Одесский национальный университет им. И.И. Мечникова
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Статы Экзамен / Статы / statukr

.pdf
Скачиваний:
80
Добавлен:
20.05.2015
Размер:
8.64 Mб
Скачать
☆

у першому випадку і

aˆk1 aˆk2 aˆk4 aˆk3 aˆk1 aˆk1 aˆk2 aˆk2

у другому. У результаті поправка (6.52) дорівнює:

 

 

ˆ

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

 

 

 

 

aˆk

aˆk aˆk aˆk

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 k k

2

 

1

1

2

2

 

(6.58)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

k1k2

 

u

 

k1k2 k1k2

 

u

 

k2k1 .

 

 

 

 

 

 

 

Оскільки k3 k4 , ясно,

що і

k1 k2. Однак

у нерівності

k1 k2 немає

необхідності,

тому

 

що

при

k1 k2 вираз

у дужках (6.58) дорівнює нулю. Через статистичну незалежність частинок ідеального електронного газу в різних станах k1 і k2 маємо:

aˆk1 aˆk1 aˆk2 aˆk2 aˆk1 aˆk1 aˆk2 aˆk2 nk1 nk2 ,

де nk – середнє число електронів у стані k. При T 0

nk kF k ,

(6.59)

де – функція Хевісайда (1.7), kF – хвильове число

Фермі. Легко зрозуміти, що при T 0 сходинку Фермі (6.59) необхідно замінити функцією розподілу (5.2), оскільки поряд із квантовомеханічним усередненням гамільтоніана (6.53) необхідно виконати також і статистичне усереднення (див. (1.30)).

Двочастинкові

матричні елементи (6.54), які входять

у формулу (6.58),

дорівнюють:

 

 

 

 

 

e2

1

 

 

k1k2

 

u

 

k1k2

 

d 3r1 d 3r2

 

 

,

 

 

V 2

r r

2

 

 

 

 

 

 

 

 

 

 

1

 

230

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(6.60)

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

e i k1 k2 r1 r2 .

 

k1k2

 

u

 

k2k1

e

1 2

d

3r1 d 3r2

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

r

r

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тут враховані

 

умови

 

ортонормування

 

 

1

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

і повноти

 

 

 

1

 

1

 

1 спінових хвильових функцій. Під-

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ставляючи матричні елементи (6.60) у (6.58), одержуємо:

 

 

 

 

 

 

 

 

ˆ

 

 

 

 

e2

nk1 nk2

d 3r1d 3r2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2V

2

 

 

r

r

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k k

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

(6.61)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i k1 k2

r1 r2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 1 2 e

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Важливо простежити за походженням доданків у (6.61). У першому з них пари операторів aˆk aˆk з однаковими інде-

ксами відповідають однаковим r у матричних елементах (6.54), а в другому – різним r . Це означає, що перший доданок у (6.61) є енергією прямої кулонівської взаємодії електронів. Другий же доданок дає внесок обмінної взаємодії електронів у їх енергію.

Інтеграл у першому доданку (6.61) розходиться. Однак через електричну нейтральність плазми цей доданок компенсується енергією взаємодії іонів між собою і з електронами. Тому згадана розбіжність інтеграла несуттєва. Обме-

жимося розглядом

внеску обмінної взаємодії електронів

у їх енергію:

 

 

 

 

 

 

 

 

Eобм

e2

nk nk

 

 

d

3r1d 3r

2

e i k1 k2 r1 r2 . (6.62)

2

 

 

r1 r2

 

V

k k

1

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

2

 

 

 

 

 

 

231

Перейдемо тут до межі V за правилом (5.6). Врахуємо вираз для компоненти Фур'є кулонівського потенціалу:

 

d 3r

e2

e iqr

 

4 e2

 

.

 

 

 

(6.63)

 

r

2

 

 

 

 

 

 

 

 

 

q

 

 

 

 

 

 

Тоді обмінна енергія (6.62) дорівнює:

 

 

 

 

 

4 e 2V

 

d 3k d 3k

 

nk nk

2

 

 

 

 

2 6

k1

k2

 

 

E

 

 

1 2

 

 

1 2

 

.

(6.64)

обм

 

 

 

 

 

 

 

 

 

 

 

 

При T 0 інтегрування в цій формулі необхідно виконувати за об’ємом кулі радіусом kF : k1, k2 kF . Переходячи до

нових змінних інтегрування

k k

1

k

2

,

k1 k2

,

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

одержуємо

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d 3k d 3k

2

 

d 3kd

3

 

 

1

 

 

 

 

 

 

,

(6.65)

 

 

2

 

k

2

 

 

 

k1 k2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

де область інтегрування задається нерівностями

k2 kF .

Вона є об’ємом між сферою Фермі і її зсунутим на k

аналогом. При фіксованому

k

 

інтеграл d 3 дорівнює

об’єму

 

 

 

 

 

 

 

 

 

 

4

 

 

3

 

 

 

 

k3

 

 

 

k3

 

 

k

2 k

 

 

 

 

 

 

 

 

3

F

 

4

F

 

16

 

 

 

 

 

 

 

цієї області. У результаті інтеграл (6.65) набуває вигляду:

232

 

d 3kd 3

4 2k 4 .

k 2

 

 

 

 

F

Тоді обмінна енергія (6.64) дорівнює:

e2k 4

Eобм V F . (6.66) 4 3

Якщо виразити тут kF через хімічний потенціал електронів згідно з (5.11) (при T 0 він дорівнює F ) і скори-

статися теоремою про малі добавки (2.44), одержимо обмінний внесок у великий потенціал електронів:

обм V e2m2 2 .

3 4

Відповідно до тієї ж теореми внесок обмінної взаємодії у вільну енергію дорівнює:

 

343

1

 

F N

 

 

e 2 n

3 ,

 

 

обм

4

13

 

 

 

 

 

де N – повне число електронів в об’ємі V , n – їх густина.

233

РОЗДІЛ 7. ФЛУКТУАЦІЇ

7.1. Флуктуації енергії і числа частинок

Відомо, що величини, які характеризують макроскопічну систему, не рівні своїм середнім значенням (1.26)– (1.28). Завдяки тепловому руху частинок вони зазнають випадкових відхилень від середніх значень, флуктують. Мірою флуктуації деякої величини F є середня квадратична флуктуація або дисперсія (1.40). Вона дорівнює:

 

 

12

 

 

 

 

12

 

 

 

 

2 12 .

F 2

 

 

 

2

 

 

 

F 2

F F

F

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рискою позначене середнє значення флуктуючої величини.

Обчислимо дисперсію енергії E 2 підсистеми з фіксо-

ваним об’ємом у термостаті. Для цього продиференціюємо середнє значення енергії

 

 

 

 

 

 

Ene

En

 

 

 

 

 

 

 

 

 

 

 

 

 

E

 

n

 

 

 

 

 

 

e

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

En

 

 

 

 

 

 

 

 

n

 

 

 

 

за оберненою температурою :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

E

 

 

 

 

 

 

 

 

E 2.

 

 

 

 

 

 

 

 

 

 

 

Переходячи тут до диференціювання

за температурою

і з огляду на співвідношення (2.25), одержуємо

 

 

 

 

 

E 2 kT 2C .

(7.1)

 

 

 

 

 

 

 

 

 

V

 

В окремому випадку класичного ідеального газу

зурахуванням (4.18) звідси знаходимо

E 2 32 N kT 2 .

234

Відносна флуктуація енергії цього газу дорівнює:

 

E 2

 

 

 

 

 

 

 

 

 

 

 

2

1

 

 

 

 

 

 

 

 

 

 

 

E

 

3

 

 

 

N

 

 

 

 

 

 

 

відповідно до результату, отриманому у підрозділі 1.6.

Щоб обчислити дисперсію N 2 числа частинок у відкритій системі, яка займає виділений об’єм V , продиференціюємо середнє число частинок

 

 

 

 

Ne

 

N

ENn

 

 

 

 

 

 

 

 

 

 

 

 

 

Nn

 

 

 

 

 

 

 

 

N

 

 

 

 

 

 

 

 

e

N ENn

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Nn

 

 

 

 

 

 

 

за хімічним потенціалом :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N

 

N 2 kT

(7.2)

 

.

 

 

 

 

 

 

 

 

 

V ,T

 

З огляду на вираз (4.25) для середнього числа частинок класичного ідеального газу, одержуємо

N 2 N.

Формули (7.1) і (7.2) справедливі як у класичному, так і у квантовому випадках. Вони не залежать від масштабу флуктуацій.

Використаємо співвідношення (7.2) для обчислення дисперсії чисел заповнення ni одночастинкових станів в іде-

альних фермі- і бозе-газах:

ni 2 kT ni .

235

Диференціюючи (5.2) і (5.78) за хімічним потенціалом, одержуємо

 

 

 

 

 

 

n

2 n

1

n

,

i

 

i

 

i

 

де верхній знак стосується ферміонів, а нижній – бозонів. Формула (7.1) може бути використана для обчислення

дисперсії енергії чорного випромінювання з частотами в інтервалі в заданому об’ємі V :

E 2 kT 2 T E ,

де E E , E – спектральна густина енергії чорного

випромінювання (5.98). Виконуючи диференціювання за температурою, одержуємо формулу Ейнштейна (1909):

 

 

 

 

2c3

 

 

2 .

E 2

 

 

 

E

E

V 2

 

 

 

 

 

 

 

Ця формула ілюструє дуалізм «хвиля–частинка». Перший доданок у правій частині обумовлений корпускулярними властивостями випромінювання, а другий – хвильовими. Якщо kT , перший доданок домінує, тобто випро-

мінювання поводиться як набір корпускул. Якщо

жkT , домінує другий доданок, випромінювання

можна розглядати як сукупність класичних електромагнітних хвиль.

7.2. Розподіл Гаусса

Розглянемо замкнуту систему. Нехай x – класична флуктуюча величина, яка характеризує систему в цілому або її частину. Будемо відраховувати величину x від її середнього значення, тобто покладемо x 0. Відхилення величини x від середнього значення означає, що система переходить

236

у стан неповної рівноваги. Статистична вага та ентропія (1.62) такого стану залежать від x . При переході рівноважної системи в стан неповної рівноваги вони зменшуються. Оскільки статвага є мірою імовірності стану системи, то імовірність знайти флуктуючу величину x у проміжку x, x dx пропорційна

e x dx,

(7.3)

де x – ентропія нерівноважного стану. Ця формула за-

пропонована для опису флуктуацій А. Ейнштейном (1907). Існує два основні джерела флуктуацій:

1)флуктуації класичних величин, обумовлені тепловим рухом обмеженого числа частинок у системі,

2)флуктуації квантових величин, пов'язані із співвідношеннями невизначеностей.

Уцьому підрозділі ми обмежимося розглядом класичних флуктуацій. Це означає, що формула (7.3) справедлива лише в тому випадку, коли

kT 1,

де – час помітної зміни величини x . Якщо і T малі, флуктуації не можна розглядати класично.

При малих флуктуаціях x ентропія x у формулі (7.3) може бути розкладена в ряд за ступенями x :

x 0

d

x

1

d 2

x2 ...

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

dx 0

 

2

 

dx

 

0

 

Тут 0 – ентропія системи в стані повної рівноваги. Похідні, відзначені індексом 0, обчислюються в цьому стані. Оскільки ентропія в стані рівноваги максимальна, то

237

d

0,

 

 

 

 

 

dx 0

 

Тоді густина імовірності дорівнює:

d 2

0.

 

 

 

 

 

 

 

dx

2

 

 

 

0

 

для

флуктуючої величини x

w x Ae

 

2

2 x

.

Константа A може бути знайдена з умови нормування

dxw x 1.

Оскільки функція w x локалізована поблизу точки x 0,

інтегрування можна виконувати за всіма значеннями x . У результаті одержуємо розподіл Гаусса:

 

 

 

 

 

 

2

 

 

 

 

e

 

w x

2 x

.

(7.4)

2

 

 

 

 

 

 

 

Середня квадратична флуктуація величини x дорівнює:

 

 

1

.

x2 dxx2w x

 

 

 

 

 

 

 

Цей вираз дозволяє функцію (7.4) записати у вигляді:

 

 

 

 

 

 

 

 

2

 

 

w x

1

 

x

 

exp -

 

.

(7.5)

 

 

 

 

 

 

 

2 x2

 

 

2x2

 

 

 

 

 

 

 

 

Графік цієї функції показаний на рис. 7.1.

238

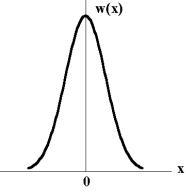
Рис. 7.1. Розподіл Гаусса

Ширина цієї кривої визначається дисперсією величини x . Якщо стан неповної рівноваги характеризується декіль-

кома флуктуючими величинами x1,..., xn , то густина імо-

вірності їх малих відхилень від рівноважних значень дорівнює:

 

 

 

 

1

ik xi xk

 

 

 

 

 

 

 

 

w x1,..., xn Ae

2 ik

,

(7.6)

 

 

 

де

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

x x

 

 

 

ik

 

 

 

 

 

 

 

i

 

k 0

 

 

– позитивно визначена симетрична матриця. Середні xi

прийняті рівними нулю. Константа A визначається з умови нормування

 

 

 

 

dx1... dxn w x1,..., xn 1.

(7.7)

 

 

 

Для обчислення цього інтеграла приведемо квадратичну форму в показнику експоненти (7.6) до діагонального вигляду перетворенням

239

Соседние файлы в папке Статы
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности