Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесский национальный университет им. И.И. Мечникова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

statukr

.pdf

Скачиваний:

Добавлен:

20.05.2015

Размер:

8.64 Mб

Скачать

☆

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 5214 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

підрозділі. Тут ми розглянемо внески обертальних і коливальних ступенів свободи в термодинамічні величини.

Оскільки молекули незалежні, обертальна статистична сума дорівнює:

Z об =( z об(1))N ,	(4.27)
де N – число молекул у системі, а z об(1)	– одночастинкова

обертальна статсума. Вона визначається рівнями енергії обертального руху молекули, розглядуваної як тверде тіло:

об(l)	2l l 1	,	(4.28)
	2J

де l 0,1,... – обертальне	квантове число, J		– головний

момент інерції молекули. Рівні (4.28) вироджені за напрямками кутового моменту молекули з кратністю 2l 1. Отже,


одночастинкова статсума дорівнює:		l l 1
	2
z об(1) 2l 1 exp			.	(4.29)
	2JkT
l 0

Звідси видно, що справедливим є своєрідний закон подібності: внесок обертального руху в термодинамічні величи-

ни як функції безрозмірної температури kTJ 2 має однако-

вий вигляд для всіх двохатомних газів. Різниця між першим збудженим рівнем обертального руху і основним рівнем

може бути записана у вигляді 2 J kT об , де T об має сенс

температури збудження обертального руху молекули. Розглянемо асимптотики суми (4.29) при низьких

і високих температурах. Якщо T << T об, у сумі (4.29) можна обмежитися двома доданками:

z об(1)		2
	1 3exp		.	(4.30)


		JkT

130

Із формул (3.14), (4.27) і (4.30) знаходимо внесок обертального руху у вільну енергію газу:

		2
F об 3NkT exp			.	(4.31)
F об 3NkT exp			.	(4.31)

	JkT

Тут ми обмежилися першим членом розкладу логарифма за ступенями малої експоненти в (4.30). Обертальна ентропія дорівнює:

				2			2
S об=		F об 3Nk exp			1
S об=	T	F об 3Nk exp			1
	T		JkT			JkT

2 2

3Nk JkT exp JkT .

Звідси видно, що при T << T об можна обмежитися диференціюванням лише експоненти в (4.31), яка швидко

змінюється. Тоді обертальна теплоємність							при T << T об
дорівнює:
			2 2			2
C об T		S об 3Nk		exp			.	(4.32)


	T
		JkT			JkT

При наближенні до абсолютного нуля теплоємність (4.32) експоненціально зменшується. У такому випадку говорять про «вимерзання» обертальних ступенів свободи. Наявність

щілини 2	J	у спектрі збудження обертального руху
		експоненціальної залежності exp
приводить до			kT

термодинамічних величин від температури.

В області високих температур T >>T об можна скористатися розкладом термодинамічних величин за ступенями T об/ T . Обмежуючись головним членом розкладу, будемо

131

вважати спектр енергії обертального руху суцільним. Це дозволяє суму (4.29) замінити інтегралом:

						2l l 1
						2l l 1
z об(1) dl 2l 1 exp							2JkT		.
0							2JkT
0
Оскільки dl 2l 1 d l	l 1 , цей інтеграл дорівнює:

z об(1)		2JkT		.					(4.33)
z об(1)				.					(4.33)
		2
У результаті
F об NkT ln			2JkT				,
F об NkT ln							,
					2
S об Nk Nk ln					2JkT			,
S об Nk Nk ln								,
					2
	E об NkT ,								(4.34)
	C об Nk .								(4.35)

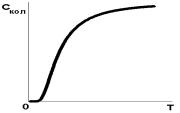
Відзначимо, що наступний член розкладу обертальної теплоємності за ступенями T об/T позитивний. Це означає, що на графіку залежності C об T при температурі ~ T об

існує максимум, схематично показаний на рис. 4.1.

Рис. 4.1. Залежність обертальної теплоємності від температури

Із формул (4.17) і (4.34) видно, що при високих температурах, коли можна застосувати класичну статистику, справедлива теорема про рівномірний розподіл енергії

132

за ступенями свободи: на кожен ступінь свободи поступального і обертального руху молекули припадає середня енергія kT 2 .

Щоб знайти внесок малих коливань атомів молекули в термодинамічні величини газу, скористаємося формулою для рівнів енергії квантового лінійного гармонічного осцилятора:

кол n		1
	n		,	(4.36)
	n		,	(4.36)
		2

де – частота коливань, n 0,1,... – коливальне квантове число. Рівні (4.36) не вироджені. Отже,

			1
		n
		n
(1)	exp		2
z кол	exp			.	(4.37)
	n 0	kT

Ця сума містить геометричну прогресію зі знаменником
exp		kT	, тому
		kT
			(1)			1
			z кол					.		(4.38)
			z кол		2sh			.		(4.38)

							2kT
Коливальна вільна енергія дорівнює:
				(1)	N
	F кол kT ln [ z кол				] NkT ln				2sh		.
	F кол kT ln [ z кол				] NkT ln				2sh		.
										2kT

Внесок коливань у внутрішню енергію газу має вигляд:

E кол NkT 2		(1)	N
		ln z кол			cth		.	(4.39)

	T			2		2kT
	T			2		2kT

133

Енергія виявилася рівною E кол N кол, де кол – середня енергія осцилятора в термостаті. Вона дорівнює:


кол			.	(4.40)
кол	2		.	(4.40)


		e kT 1
		e kT 1

Перший доданок у цій формулі являє собою енергію нульових коливань атомів у молекулі, а другий – енергію збудження.

З формули (4.39) одержуємо внесок коливань у теплоємність газу:

					2

			2kT
C кол		E кол Nk			.	(4.41)

	T

		sh

				2kT

Відстань між рівнями енергії осцилятора пов'язана з температурою збудження T кол коливального руху співвідношенням k T кол. Із формул (4.40) і (4.41)

випливає, що:


			exp		,	T Tкол ,
		2	exp		,	T Tкол ,
кол		2		kT		(4.42)
	kT ,					T T ,
						кол



Nk
C кол

Nk,

2				T Tкол
	exp		,		,	(4.43)

kT		kT
				T Tкол	,

Графік залежності C кол T наведено на рис. 4.2.

Як і у випадку обертального руху, коливальні ступені свободи «вимерзають» при низьких температурах. Із формули (4.42) видно, що в області високих температур на

134

кожен коливальний ступінь свободи припадає середня енергія kT .

Рис. 4.2. Залежність коливальної теплоємності від температури

4.4. Магнетизм газів

Будемо вважати, що частинки ідеального газу мають

магнітні моменти і газ перебуває в зовнішньому постій-

ному і однорідному магнітному полі H . Енергія частинки

містить доданок H , який повинен бути врахований при

розрахунку термодинамічних величин. Магнітне поле на-

магається впорядкувати магнітні моменти частинок, орієн-

туючи їх уздовж вектора H , а хаотичний тепловий рух перешкоджає впорядкуванню. У результаті встановлюється деяка середня намагніченість газу, спрямована вздовж магнітного поля. Обчислимо її, нехтуючи просторовим квантуванням магнітного моменту.

Кожна частинка газу подібна ротатору, який виконує поступальний і обертальний рух. Як і в попередньому підрозділі, статистичний інтеграл газу дорівнює:

Z = Z пост Z рот ,

де

Z рот=( z рот(1))N.

У результаті термодинамічні величини газу містять доданки, зумовлені обертанням магнітних моментів частинок

135

відносно вектора H . Саме ці внески нас цікавлять у цьому підрозділі.

Орієнтацію вектора у просторі зручно задавати кутами і сферичної системи координат з віссю z, спрямованою уздовж магнітного поля. Цим кутам відповідають спряжені імпульси p і p . Оскільки ротатор має два сту-

пені свободи, його фазовий простір чотиривимірний. Одночастинковий статистичний інтеграл ротатора дорівнює:

	1		2
(1)	1		d d		dp	dp exp (– рот/k),
z рот								(4.44)
z рот	2	2						(4.44)
	2		0	0
де
				p2	p2
			рот				Hcos	(4.45)
			рот		2J sin2		Hcos	(4.45)
				2J	2J sin2

– енергія ротатора в магнітному полі, J – його головний момент інерції. Підставляючи (4.45) у (4.44) і враховуючи інтеграл (4.2), одержуємо:

	(1)		JkT				H cos
	z рот			d sin exp						.
	z рот		2	d sin exp					kT	.
				0					kT
				0
Цей	інтеграл обчислюється за						допомогою			підстановки
x cos . У результаті –
			(1)		2JkT	sh H
		z	рот				kT	.		(4.46)
		z	рот		2			.		(4.46)
					2		H
							kT
Якщо	магнітне	поле		відсутнє,			вираз		(4.46) збігається

з (4.33).

Обертальна частина вільної енергії газу дорівнює:

136

схематично зображена на рис. 4.3.

		sh	H
	2JkT	sh	kT
F рот NkT ln			kT	.	(4.47)
F рот NkT ln	2	H		.	(4.47)
		H

		kT

Як і слід було чекати, вона адитивна. Адитивна і внутрішня енергія:

E рот N рот ,

де

		(1)		1 H		H

рот kT 2		ln z рот	2kT 1		cth		(4.48)

	T
				2 kT		kT

– середня обертальна одержуємо ротаційну на частинку:

c рот

Якщо врахувати

shx

енергія однієї частинки. Із (4.48) частину теплоємності в розрахунку

рот k 2

(4.49)

, x 1,

exp x, x 1,

із формули (4.49) одержуємо асимптотики теплоємності:

	H		2			2	H
k 2	4			exp		2	, kT H,
	kT						kT
								(4.50)
c рот					2			(4.50)
		1		H	2
	k 1	1		H		,	kT H.


		3		kT

Залежність c рот T

137

Рис. 4.3. Теплоємність ротаторів у магнітному полі

Формула (4.50) має простий фізичний зміст. У слабкому магнітному полі ротатор виконує вільне обертання. Оскільки він має два обертальні ступені свободи, відповідно до теореми про рівнорозподіл енергії його внесок у теплоємність c рот дорівнює k . У сильному магнітному полі магнітний момент кожної частинки виконує малі коливання біля напрямку поля. Оскільки існує два коливальні ступені свободи, внесок молекули в теплоємність дорівнює 2k .

Середній магнітний момент газу дорівнює:

(4.51)

T ,N

де M –

намагніченість газу,

– його об’єм. Диферен-

ціюючи (4.47), одержуємо формулу Ланжевена:

(4.52)

M nL

де n N

– густина газу,

L x cthx

(4.53)

– функція Ланжевена. Оскільки

x 1,

cthx

1, x 1,

138

із формули (4.52) знаходимо асимптотики

H,			H kT ,
M	n,		H kT ,		(4.54)
	n,		H kT ,
де
	M		2n		(4.55)
	H		3kT		(4.55)
	H		3kT
– магнітна сприйнятливість. Залежність C				T	називаєть-
				T
ся законом Кюрі, а
C		2n			(4.56)
C		3k			(4.56)

– постійною Кюрі. Із (4.54) видно, що, лінійно зростаючи з полем у слабких магнітних полях, намагніченість досягає насичення в сильному полі.

Врахуємо просторове квантування магнітного моменту частинки. Із квантової механіки відомо, що проекція магнітного моменту атома на магнітне поле дорівнює g Bm , де

g 1		J J 1 L L 1 S S 1
		2J J 1

– фактор Ланде ( L , S і J – квантові числа орбітального,
спінового і повного моментів атома), B – магнетон Бора,
m J , J 1,..., J		– магнітне квантове число. Енергія

атома в магнітному полі, яка дорівнює g BmH , визначає магнітну частину статистичної суми газу:

	ZH zH1 N ,					(4.57)
де
zH1	J	g		B	mH
	exp			B
	exp		kT
	m J		kT

139

<<< < Предыдущая 2 3 4 5 6 7 8 9 10 11 12 1314 / 5214 15 16 17 18 19 20 21 22 23 24 25 26 > Следующая >>>

Соседние файлы в папке Статы

#
20.05.2015868 Кб3IMG_20140520_205259_193.jpg
#
20.05.20151.68 Mб3IMG_20140520_205307_970.jpg
#
20.05.20151.64 Mб3IMG_20140520_205317_302.jpg
#
20.05.20151.11 Mб3IMG_20140520_205328_574.jpg
#
20.05.20151.03 Mб3IMG_20140520_205339_012.jpg
#
20.05.20158.64 Mб80statukr.pdf