Статы Экзамен / Статы / statukr

h можна трактувати як квант площі. Площа, що припадає на один мікростан, дорівнює h. Отже, число мікростанів на елементі площі dxdpx дорівнює

dxdpx . h

Якщо система має велике число r ступенів свободи, ця формула виглядає так:

де d – елемент об’єму у фазовому просторі системи. Отриманий результат відповідає співвідношенням невиз-

наченості Гейзенберга (1.4). З них випливає, що мікростан системи у квазікласиці можна зіставити з коміркою об’є-

мом hr у фазовому просторі. Деталізувати положення фаової точки всередині цієї комірки неможливо.

Якщо у формулі (1.6) перейти до квазікласики (це виведення тут опущене), одержимо:

Тут H q, p E – рівняння поверхні (гіперповерхні) по-

припадає на один мікростан. Зміст формули (1.10) очевид-

21

ний, і тільки поява N ! у знаменнику потребує пояснення. Справа в тому, що в класичній механіці навіть однакові

частинки можна розрізнити. Перестановка частинок системи дає іншу фазову точку у фазовому просторі, іншу комірку. Між тим, з квантової точки зору, однакові частинки розрізнити не можна, тобто мікростани, які ми отримуємо при перестановці частинок, повинні розглядатися як один мікростан. При підрахунках числа комірок у (1.10) усі комірки, отримані при перестановці частинок, повинні враховуватися тільки один раз. А оскільки інтегрування в (1.10) виконується за всім об’ємом всередині поверхні постійної енергії, результат інтегрування необхідно розділити на число перестановок частинок N !.

У формулі (1.10) можна перейти до інтегрування за всім фазовим простором:

мікростанів квантової системи з енергією усередині цього проміжку дорівнює:

сиці ця формула набуває вигляду:

22

називається статистичною вагою макростану системи, заданого величинами V , E, E .

1.2.2. Густина станів

Статвагу (1.12) можна представити у вигляді

W E, E E E E .

– густина станів. Вона має сенс числа станів в одиничному енергетичному проміжку. З огляду на формулу для - функції:

Видно, що перехід до квазікласики здійснюється заміною підсумовування за квантовими станами інтегруванням за

23

Якщо густина станів відома, то число станів може бути знайдене згідно з формулою

перетворення Лапласа для густини станів має вигляд:

z dE E e E ,

0

де i – комплексне число. З огляду на формулу

(1.17), одержуємо:

z e En .

n

Якщо функція z відома, густина станів може бути отримана із оберненого перетворення Лапласа:

де число a вибирається так, щоб усі особливості функції z лежали ліворуч контуру інтегрування.

Наприклад, обчислимо густину станів частинки в тривимірній нескінченно глибокій потенціальній ямі об’ємом

24

Vl3 . Обмежимось квазікласичним випадком. Рівні енергії частинки задаються формулою:

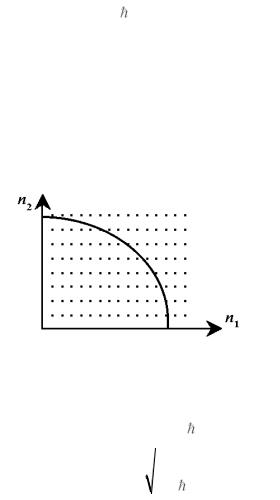
де ni 1,2,..., i 1,2,3. Мікростан частинки зображується трійкою квантових чисел n1, n2 , n3 . Зіставимо його з точкою

осі у двовимірному просторі. Кожному мікростану відповідає точка або комірка у цьому просторі.

Рис. 1.4. Мікростани частинки

Рівняння поверхні постійної енергії в цьому просторі

рис. 1.4. У квазікласичному випадку ni 1 під поверхнею

сфери міститься велика кількість комірок. Тому можна не звертати уваги на ті комірки, які лише частково знаходяться всередині кулі. Число комірок-станів усередині однієї

25

восьмої об’єму кулі дорівнює:

Звідси знаходимо густину станів частинки:

Вона пропорційна квадратному кореню з енергії частинки. Використовуючи метод Лапласа, обчислимо густину

станів сферичного маятника, який підкоряється законам класичної механіки. Його гамільтонова функція дорівнює

26

Густина станів маятника пов'язана з цією функцією співвідношенням:

де a 0 .

Якщо 0 mgl , то в першому доданку в правій

частині цієї рівності контур інтегрування замикаємо в лівій напівплощині комплексної змінної , а в другому додан-

ку – у правій напівплощині. Одержуємо

Якщо ж mgl , то в обох доданках замикаємо контур інтегрування в лівій напівплощині. Тоді одержуємо

Поєднуючи ці формули, знаходимо остаточно:

де – функція Хевісайда (1.7).

1.3. Функція розподілу

Мікростан класичної системи в будь-який момент часу може бути знайдений за рівняннями Гамільтона (1.1), якщо він відомий у початковий момент. Ясно, що проінтегрувати величезну кількість рівнянь руху механічної макросистеми практично неможливо. І навіть якби це виявилось можли-

27

вим, не можна було б визначити сталі інтегрування. Щоб знайти їх, необхідно знати початковий мікростан системи q 0 , p 0 . Однак в жодному реальному експерименті

одержати ці величини неможливо. Тому ми змушені відмо-

Будемо вважати величини q, p випадковими. Про них

відомо, що координати частинок системи лежать в об’ємі V, який обмежує систему, а кожна компонента імпульсу може мати будь-яке значення між і . Згідно з теорією імовірностей введемо функцію розподілу f q, p для

величин q і p . Щоб її ввести, розглянемо елемент об’єму d dqdp у фазовому просторі системи. Ясно, що, рухаю-

чись, фазова точка системи буде багаторазово повертатися в цей об’єм. На рис. 1.5 показана ділянка фазової траєкторії системи.

Рис. 1.5. Фазова траєкторія системи

На ній немає точок самоперетину і дотикання. Наявність таких точок суперечила б однозначності розв’язку рівнянь руху системи. Нехай dt – час перебування фазової точки в об’ємі d , а Т – час спостереження над системою. Тоді величина

28

lim dt dw

T T

є імовірністю того, що при спостереженні над системою

– густина імовірності стану системи. Вона має сенс імовірності перебування фазової точки в одиничному фазовому об’ємі. Величина f залежить від координат q, p

об’єму d . Якщо система нерівноважна, її функція розподілу явно залежить також від часу: f q, p,t .

Визначена в такий спосіб функція розподілу відмінна від нуля, позитивна і неперервна. У випадку замкнутої системи неперервність випливає з так званої квазіергодичної гіпотези. Відповідно до цієї гіпотези, фазова траєкторія з часом проходить як завгодно близько до будь-якої точки на поверхні постійної енергії. Траєкторія замкнутої системи – скрізь щільна множина на гіперповерхні H q, p E , але

не збігається з нею. Якщо ж система перебуває в середовищі, згадана властивість функції розподілу пов'язана з заплутаністю фазової траєкторії, обумовленою випадковим впливом середовища.

Функція розподілу задовольняє умову нормування

де інтегрування виконується за всім фазовим простором

29

системи. Якщо проінтегрувати функцію розподілу тільки за імпульсами, одержимо розподіл за координатами у конфігураційному просторі:

f q dpf q, p .

Інтегрування за координатами дає функцію розподілу в імпульсному просторі:

f p dqf q, p .

Якщо система достовірно перебуває в певному мікростані q0 , p0 , то функція розподілу дорівнює:

r

f q, p qi q0i pi p0i .

i 1

Часто функцію розподілу q, p нормують умовою

Видно, що f і відрізняються постійним множником.

При такому способі нормування імовірність знайти фазову точку в об’ємі d дорівнює

d q, p . h3N N !

Причини появи імовірностей у квантовій статистиці аналогічні. Оскільки величини повного набору n макросистеми одержати практично неможливо, ми змушені вважати їх випадковими величинами і вводити квантову функцію розподілу n . Вона має сенс імовірності того, що

величини n мають задані значення. Функція n задовольняє умову нормування

30