
Статы Экзамен / Статы / statukr
.pdf
У граничному випадку H=0, = при фіксованому числі електронів з цієї формули одержуємо:
Nm F S ,
2
де F – енергія Фермі двовимірного електронного газу. Ця
формула випливає з (5.12), якщо врахувати вираз для густини електронних станів
mS
2 2
у двовимірному випадку. Остання легко може бути отримана із загальної формули (1.17).
5.8.Розподіл Бозе – Ейнштейна
Уцьому підрозділі ми одержимо функцію розподілу частинок за станами в ідеальному бозе-газі. Як і у випадку
ферміонів, стан |
i |
частинки характеризується її імпульсом |
|
|
|
p і спіновим квантовим числом : i p, . Спін частин-
ки s 0, 1, 2, ... має g 2s 1 орієнтацій у просторі. Оскільки бозони не підкоряються принципу Паулі, числа заповнення ni одночастинкових станів можуть мати будь-які цілочисельні значення: ni 0, 1, 2, ... Закон дисперсії час-
тинки, як і раніше, будемо вважати параболічним (1.2). Щоб знайти середнє число бозонів ni у стані i , застосу-
ємо до частинок у цьому стані великий канонічний розподіл Гіббса. Їхня енергія дорівнює ni i , де i – енергія
однієї частинки. Великий потенціал (3.5) цих частинок дорівнює:
190
|
i ni |
|
|
i kT ln e |
kT |
. |
(5.86) |
|
ni 0
Сума, що входить сюди, являє собою геометричну прогресію зі знаменником
exp i .
kT
Вона сходиться, якщо
0 . |
(5.87) |
Таким чином, хімічний потенціал ідеального бозе-газу не може бути позитивним. Виконуючи в (5.86) підсумовування, одержуємо
|
|
|
- i |
|
|
|
i |
kT ln 1 e kT |
. |
(5.88) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Великий потенціал усього газу дорівнює
|
|
i |
i kT ln 1 e kT |
||
|
|
|
i |
i |
|
. (5.89)
Середнє число частинок у стані i знаходимо за допомогою формули (2.93):
n i |
|
1 |
|
. |
(5.90) |
|
|
|
|||||
i |
|
|
i |
|
|
|
|
|
1 |
|
|||
|
|
|
e kT |
|
||
Цей вираз називається функцією розподілу Бозе – Ейнштейна.
Якщо |
|
|
|
|
|||
|
|
|
|
|
|
1, |
|
|
|
||||||
exp |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|||
kT |
|
||||||
191
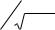
розподіл (5.90) переходить у класичний розподіл Больцмана (4.26). Підставляючи в цю нерівність хімпотенціал (4.22), перепишемо його у вигляді (5.5). Як і у випадку фер- мі-газу, квантовий розподіл (5.90) переходить у класичний (4.26), якщо теплова довжина хвилі де Бройля частинки
|
|
мала у порівнянні із середньою відстанню між |
|
mkT |
|
|
|
частинками газу. |
|
Повне число частинок у газі дорівнює |
|
N ni . |
(5.91) |
i |
|
Якщо воно фіксоване, це рівняння дозволяє визначити хімічний потенціал бозонів як функцію густини і темпера-
тури. |
|
|
|
Оскільки індекс i p, входить до функції розподілу |
|
тільки через енергію, суми (5.89) і (5.91) можуть бути замінені інтегралами за вже відомим правилом:
|
|
d , |
|
|
|
||
g |
|
(5.92) |
|
i p |
0 |
|
|
де – густина станів (1.20). Вона визначається законом дисперсії частинки (1.2).
5.9. Бозе-ейнштейнівська конденсація
Оскільки бозони не підкоряються принципу Паулі, при нульовій температурі усі вони перебувають у стані з нульовим імпульсом. Координати кожної частинки при цьому цілком не визначені. Частинка з рівною імовірністю може бути знайдена в будь-якій точці конфігураційного простору. Сукупність частинок у стані з нульовим імпульсом називається бозе-ейнштейнівським конденсатом. З'ясуємо,
192

як утворюється конденсат при зменшенні температури бозе-газу.
Якщо температура настільки висока, що газ підкоряється законам класичної статистики, розподіл частинок в імпуль-
сному просторі схожий на хмару. Вона |
більш густа на |
|
p густина хмари |
початку координат p 0. При збільшенні |
зменшується відповідно до формули Максвелла (4.3). Коли
температура знижується, |
розміри хмари зменшуються, |
і при деякій температурі T0 |
виникає нове явище. Частинки |
починають накопичуватися в стані з нульовим імпульсом. При T T0 число частинок у нескінченно малому елементі
об’єму імпульсного простору на початку координат нескінченно мале. Якщо ж T T0 , це число виявляється обмеже-
ним. При подальшому зниженні температури все більше |
|
|
і при T 0 усі |
число частинок переходить у стан p 0 |
|
вони виявляються в конденсаті. Утворення конденсату – квантовий ефект. Тому для з'ясування природи температури T0 необхідно порівняти теплову довжину хвилі де Брой-
ля частинки |
|
|
із середньою відстанню |
V |
N |
13 |
між |
mkT |
|
||||||
|
|
|
|
|
|
ними. Якщо T T0 , довжина хвилі де Бройля мала у порів-
нянні з відстанню між частинками. У цьому випадку квантовими ефектами можна знехтувати. Якщо ж T T0 , ці дов-
жини зрівнюються, і рух частинок необхідно описувати законами квантової механіки. З умови
|
|
|
|
V 13 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
||||
|
mkT0 |
N |
|||
одержуємо
193

|
|
|
|
|
T0 |
|
2 |
N |
23 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
(5.93) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
mk V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Переходячи |
у формулі |
(5.91) |
від |
підсумовування за |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
одержуємо |
|
i p, до інтегрування за правилом (5.92), |
|||||||||||||||||||||||||||
рівняння для хімічного потенціалу бозонів: |
|
|
|||||||||||||||||||||||||
|
|
|
|
g |
mkT |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
N |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||
|
|
|
2 |
dx |
|
|
|
|
|
|
. |
|
|
(5.94) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
V |
|
|
2 2 3 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
0 |
|
|
x |
|
|
|
|
|
1 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
kT |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Тут введена нова змінна інтегрування |
x |
|
kT |
і врахована |
|||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нерівність (5.87). Припустимо, що густина частинок фіксована, і будемо поступово знижувати температуру. Тоді
інтеграл у |
(5.94) повинен зростати. Отже, |
відношення |
||||||
|
|
|
kT повинно зменшуватися. Коли величина |
|
|
|
kT дося- |
|
|
|
|
|
|||||
|
|
|
|
|||||
гає свого |
граничного значення, рівного нулю, інтеграл |
|||||||
у (5.94) стає максимальним. Це відбувається при деякій кінцевій температурі T0 . Вона не може дорівнювати нулю,
тому що тоді рівність (5.94) буде порушено. Із (5.94) одержуємо рівняння для T0 :
|
|
|
|
|
|
g mkT0 |
3 |
2 |
|
|
|
|
|
|
|
|
||||||
|
|
N |
|
|
|
|
x |
|
|
|
||||||||||||
|
|
|
|
|
|
dx |
|
|
|
. |
(5.95) |
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
x |
|
|
|
|
||||
|
|
V |
|
|
|
2 |
|
|
0 |
e |
|
1 |
|
|||||||||
Оскільки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dx |
x |
|
|
z z |
|
|
z 1 , |
|
|||||||||||||
|
x |
|
|
|
|
|
||||||||||||||||
|
0 |
|
|
e |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де z – |
дзета-функція Рімана 3 |
2 |
2, 612 , |
із (5.95) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
знаходимо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
194

|
|
1 |
2 |
3 |
2 |
N |
23 |
|
||
T |
3,31 |
|
|
|
|
|
|
|
. |
(5.96) |
|
|
|
|
|||||||
0 |
|
|
|
|
mk V |
|
|
|||
|
g |
|
|
|
|
|||||
Видно, що цей вираз за порядком величини збігається з отриманим вище виразом (5.93).
При T T0 рівняння (5.94) уже не виконується ні при якому 0 . Справа в тім, що при переході від (5.91) до (5.94) врахована густина станів 
 . Вона зникає в точці 0 , тим часом як саме в цій точці накопичуються частинки при T T0 . Функція розподілу частинок за енергією з густиною станів (1.20) справедлива лише для станів
. Вона зникає в точці 0 , тим часом як саме в цій точці накопичуються частинки при T T0 . Функція розподілу частинок за енергією з густиною станів (1.20) справедлива лише для станів
0 . При T T0 вона дорівнює: |
|
|
|
|
|
|||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
dN 0 |
|
gVm |
2 |
|
|
d |
. |
|||||
|
|
|
|
2 3 |
|
|
|
|
||||
|
2 |
|
|
|||||||||
|
|
|
|
e kT 1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Тоді число частинок у станах 0 (надконденсатні частинки) при T T0 дорівнює:
|
|
|
|
mkT 32 |
dx |
|
|
|
|
|
N 0 |
|
gV |
|
x |
. |
|||||
|
|
|
|
|
||||||
2 2 3 |
||||||||||
|
|
|
|
ex 1 |
||||||
|
|
|
|
|
0 |
|
|
|
|
|
З огляду на (5.95), одержуємо звідси:
|
|
T |
|
32 |
|
N 0 |
N |
. |
|||
|
|||||
|
T0 |
|
|
||
Число частинок у конденсаті при T T0 |
дорівнює: |
|||||||
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
||||
N 0 |
N N 0 |
N 1 |
T |
|
|
|
. |
|
|
|
|
||||||
|
|
|
T0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Графіки функцій (5.97) і (5.98) показані на рис. 5.10.
(5.97)
(5.98)
195

Рис. 5.10. Залежність числа частинок у конденсаті і числа надконденсатних частинок від температури
Відзначимо, що в цьому підрозділі йдеться про конденсацію в імпульсному просторі, а не про зближення частинок ідеального бозе-газу в конфігураційному просторі. У 1995 році бозе-ейнштейнівська конденсація була виявлена експериментально М. Андерсоном та ін. у парах лужно-
земельних металів при температурах, менших 10 6 K .
5.10. Термодинамічні функції виродженого бозе-газу
Бозе-газ при температурах T T0 називається виродже-
ним. Оскільки частинки конденсату мають нульову енергію, внутрішня енергія газу при T T0 визначається лише
надконденсатними частинками. Вона дорівнює:
|
|
|
|
|
|
|
1 |
|
|
|
|||
|
|
|
|
E ini g d |
|
. |
(5.99) |
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
i |
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
ekT |
|
||||||
|
|
|
|
|
|
|
|
|
|||||
Переходячи |
до нової |
змінної x |
|
kT |
і з |
огляду на |
|||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,341 |
, із (5.99) одержуємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
196
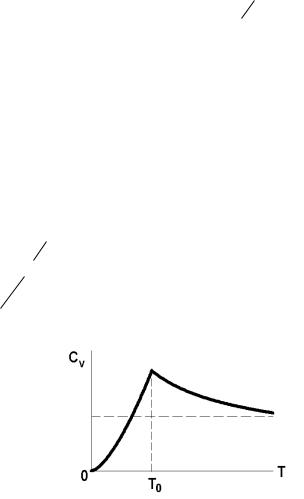
|
T |
|
32 |
|
|
E 0, 77NkT |
|
. |
(5.100) |
||
|
|||||
T0 |
|
|
|
||
Зменшення енергії газу (5.100) у порівнянні з класичним значенням (4.17) обумовлене існуванням конденсату, який не дає внеску в енергію.
Диференціюючи (5.100) за температурою, одержуємо теплоємність газу при постійному об’ємі:
|
E |
|
5 E |
|
||
CV |
|
|
|
|
|
. |
|
|
|
||||
|
T |
|
2 T |
|
||
|
V |
|
|
|
|
|
При зниженні температури вона зменшується за законом
C |
T 3 2 . Відзначимо, що при температурі T |
похідна |
|
V |
|
0 |
|
CV |
T має стрибок. |
Відповідний злам на кривій CV T |
|
показаний на рис. 5.11.
Рис. 5.11. Теплоємність бозе-газу
Якщо T T0 , теплоємність досягає класичного значення
(4.18).
Якщо у формулі (5.89) врахувати правило (5.92), великий потенціал ідеального бозе-газу може бути записаний у вигляді:
197
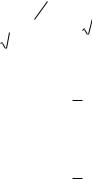
|
|
|
|
3 |
|
|
|
|
- |
|
|
gVm 2 |
|
||||||||
|
|
|
|
|
||||||
|
|
|
|
|||||||
kT |
|
|
|
|
|
|
d ln 1 |
e kT |
||
|
|
|
2 |
|
3 |
|||||
|
2 |
|||||||||
|
|
|
|
0 |
|
|
|
|||
.
Виконуючи тут інтегрування за частинами, одержуємо:
23 E .
Це співвідношення збігається з (5.31) і справедливе при будь-якій температурі. З урахуванням (2.94) знаходимо:
PV 23 E .
Підставляючи сюди (5.100) і з огляду на (5.95), переконаємося в тому, що при T T0 тиск бозе-газу не залежить від
об’єму. Це означає, що його стисливість стає нескінченною.
Якщо T T0 , великий |
потенціал збігається з |
вільною |
||||||
енергією: F . Тоді ентропія |
ідеального газу |
бозонів |
||||||
дорівнює: |
|
|
|
|
|
|
|
|
|
F |
|
|
5 E |
|
|
||
S |
|
|
|
|
|
|
. |
|
|
|
|
|
|
||||
|
T V |
|
|
3 T |
|
|
||
Відповідно до теореми Нернста, вона стає рівною нулю при нульовій температурі.
З формул (2.93) і (5.89) легко одержати наступний точний вираз для ентропії ідеального бозе-газу:
S k |
1 n |
ln 1 n |
n ln n |
, |
|
|
|
i |
i |
i i |
|
i
справедливий при будь-яких температурах.
5.11. Чорне випромінювання
Розглянемо порожнину в тілі. Оскільки атоми тіла випромінюють і поглинають електромагнітні хвилі, порож-
198

нина буде наповнена електромагнітним випромінюванням. Випромінювання, яке перебуває в рівновазі з речовиною, називається чорним, або рівноважним, випромінюванням. Як і речовина, воно має деяку температуру T .
Електромагнітне поле в порожнині можна розглядати як суперпозицію плоских монохроматичних хвиль:
|
|
aei qr t |
, |
де |
|
|
|
a |
– амплітуда хвилі, q і – хвильовий вектор і часто- |
||
та. Електромагнітні хвилі у вакуумі поперечні. Отже, плос-
ка монохроматична хвиля |
характеризується |
хвильовим |
|
|
і дискретним |
індексом j 1, 2 , |
який задає |
вектором q |
|||
поляризацію хвилі. Індекс одночастинкового стану |
i , який |
|
Часто- |
фігурує в підрозділі 5.8, вибираємо рівним i q, j . |
|
|
|
та хвилі залежить від індексу i : j q . У випадку електро- |
|
магнітних хвиль у вакуумі ця залежність така: |
|
cq |
(5.101) |
для хвиль з будь-яким значенням j . Тут c – швидкість
світла у вакуумі. Із формули (5.101) видно, що ізочастотними поверхнями в просторі хвильових векторів є сфери
радіуса c . Наявність меж порожнини приводить до того,
що хвильові вектори і частоти хвиль дискретні. Хвилю
з даним q можна зіставити в просторі хвильових векторів з коміркою об’ємом
2 3 ,
V
де V – об’єм порожнини. Отже, число хвиль в об’ємі d 3q q -простору дорівнює:
199
