Статы Экзамен / Статы / statukr

(5.102)

Це співвідношення справедливе для хвиль будь-якої природи: електромагнітних, звукових, хвиль де Бройля. Якщо врахувати закон дисперсії хвиль (5.101), із формули (5.102) одержимо число хвиль фіксованої поляризації з частотами в інтервалі , d :

V 2 (5.104)

2c3

–функція розподілу власних частот електромагнітного поля в порожнині.

Із квантової механіки відомо, що електромагнітне поле квантоване. Його можна розглядати як набір фотонів,

Фотони є частинками Бозе, тому що спін фотона дорівнює одиниці. Числа заповнення фотонів дорівнюють ni 0, 1, 2, ... Фотони утворюють ідеальний бозе-газ з ну-

льовим хімічним потенціалом. Справді, число фотонів у порожнині не фіксоване, а залежить від температури. Із підрозділу 2.7 випливає, що, якщо V і T задані, а фотонний газ прямує до стану рівноваги, рівноважне число фотонів може бути знайдене з умови мінімальності вільної енергії

200

Але, згідно з (2.87), ця похідна дорівнює хімпотенціалу фотонного газу. Він дорівнює нулю при будь-якій температурі. Це означає, що середнє число фотонів у стані i дорівнює:

Цю функцію називають функцією розподілу Планка. Оскільки число коливань у порожнині з частотами в ін-

тервалі d дорівнює d , а середнє число фотонів, яке припадає на одне коливання, дорівнює n , середнє число фотонів в об’ємі V дорівнює:

201

Із підвищенням температури число фотонів у порожнині

зростає пропорційно T 3 .

Енергія фотонів з частотами в інтервалі d дорівнює:

– спектральна густина енергії чорного випромінювання. Із

(5.110) видно, що

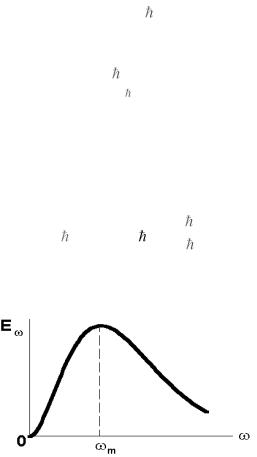
Графік функції (5.110) показаний на рис. 5.12.

Рис. 5.12. Спектральна густина енергії чорного випромінювання

При низьких частотах з формули Планка (5.110) ми одержали закон Релея – Джинса E kT . Він відповідає

теоремі про рівномірний розподіл енергії за ступенями свободи. Залежність

202

при високих частотах називається законом Віна. Положення максимуму m спектральної густини (5.110)

знаходимо з умови

dE 0 . d

Знову вводячи змінну (5.108), одержуємо для xm m kT

рівняння

3 x 3e x .

Його корінь xm 2,8 . Отже, із підвищенням температури

максимум кривої на рис. 5.12 зміщується в область високих частот пропорційно температурі (закон зсуву Віна).

Інтегруючи (5.109) за усіма частотами і знову переходячи до змінної (5.108), одержуємо внутрішню енергію фотонного газу

Співвідношення (5.111) називається законом Стефана – Больцмана. Теплоємність чорного випромінювання:

203

Із підвищенням температури вона збільшується пропорційно T 3 .

Великий потенціал фотонного газу ми одержимо з формули (5.89), у якій необхідно покласти 0 і перейти від

підсумовування за i до інтегрування за частотами:

d .

i qj 0

Виконуючи інтегрування за частинами, одержуємо

E3 .

Зурахуванням (2.94) і (5.111) знаходимо тиск чорного випромінювання:

P 43c T 4 .

Оскільки хімпотенціал фотонного газу дорівнює нулю, великий потенціал збігається з вільною енергією:

F E3 .

Отже, ентропія чорного випромінювання дорівнює:

При T 0 вона онулюється відповідно до теореми Нернста.

5.12. Модель Дебая

204

Застосуємо статистику Бозе – Ейнштейна до розрахунку термодинамічних функцій твердого тіла. Розглянемо просту кубічну решітку, яка складається з N атомів в об’ємі V . Припустимо, що спектр частот пружних коливань атомів у цій решітці такий же, як і в однорідному ізотропному суцільному середовищі. У такому середовищі можуть поширюватися: повздовжня хвиля із законом дисперсії

де ul – швидкість повздовжнього звуку, дві поперечні хвилі із спектром частот

Тут ut – швидкість поперечного звуку. Оскільки спектри

Підсумовуючи внески повздовжньої і поперечної гілок (5.115), знаходимо для повного числа хвиль з частотами в інтервалі d вираз d , де

Решітка, яка містить N точкових атомів, має 3N ступені свободи. Із них три відповідають поступальному руху кристала, а три – обертальному. Число коливальних ступе-

205

нів свободи дорівнює 3N 6 3N , тому що N 1 . Це число повинно збігатися з інтегралом від (5.116) за частотами. Отже, межі інтегрування необхідно обмежити деякою максимальною частотою Д . Вона називається дебаївсь-

кою частотою і знаходиться з умови

Д

3N d .

0

Підставляючи сюди (5.116), одержуємо

Д uqД ,

де

q6 2 N 13

Д V

–дебаївське хвильове число. Використана тут модель кристала називається моделлю Дебая. У спектрі коливань

атомів у цій моделі присутня лише одна смуга 0, Д .

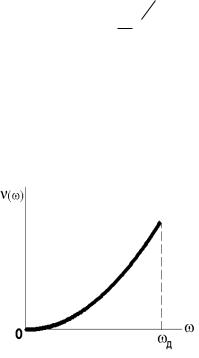
Графік функції (5.116) у моделі Дебая показаний на рис.

5.13.

Рис. 5.13. Густина станів у моделі Дебая

206

Пружні хвилі в кристалі, як і електромагнітні хвилі, квантуються. Кванти коливань називаються фононами. Імпульс і енергія фонона пов'язані з хвильовим вектором і частотою хвилі співвідношеннями (5.105). Як і фотони, фонони є бозонами з нульовим хімпотенціалом. Якщо враховуються лише гармонічні коливання решітки, газ фононів буде ідеальним. Його функція розподілу дорівнює

(5.106).

Енергія фононів при температурі T дорівнює:

Переходячи тут до змінної (5.108), одержуємо:

Якщо T , верхню межу в інтегралі (5.118) можна покласти рівною нескінченності. Тоді, з огляду на значення інтеграла (5.112), знаходимо:

Теплоємність кристала в цьому наближенні дорівнює:

Залежність CV T 3 називається законом Дебая.

207

Якщо T , функцію n у формулі (5.106) можна покласти рівною kT . Тоді з (5.117) одержуємо

E 3NkT

відповідно до теореми про рівномірний розподіл енергії за ступенями свободи. Якщо T , теплоємність кристала дорівнює:

СV 3Nk

– закон Дюлонга і Пті.

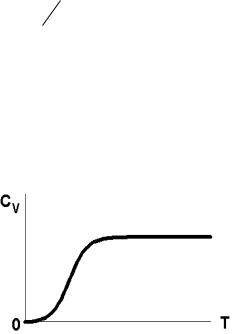
Рис. 5.14. Залежність теплоємності решітки від температури

На рис. 5.14 схематично показаний внесок фононів у теплоємність твердого тіла в моделі Дебая.

208

РОЗДІЛ 6. НЕІДЕАЛЬНИЙ ГАЗ

6.1.Часткові функції розподілу

Уцьому розділі розглядається рівноважна система N точкових частинок в об’ємі V . Враховується взаємодія частинок між собою. Спочатку передбачається, що частинки підкоряються законам класичної механіки. Для опису цієї системи в підрозділі 1.3 була введена N -часткова функція

розподілу fN X , де X q, p x1, ..., xN – координати точки у фазовому просторі системи, а xi – у фазовому просторі i -ї частинки. Величина fN dX є імовірністю того, що фазова точка системи знаходиться в елементі об’ємом

dX dx1...dxN

її фазового простору. Функція fN задовольняє умову нормування (1.21)

dX fN X 1 .

Вона підкоряється рівнянню Ліувілля, розв’язати яке так само важко, як і знайти розв’язок системи рівнянь Гамільтона.

У наступному підрозділі ми побачимо, що для обчислення термодинамічних величин, які нас цікавлять, немає необхідності визначати N -часткову функцію розподілу. Часто досить обмежитися більш простими одночастковою, двочастковою і т. д. функціями розподілу. Вони введені М. М. Боголюбовим у 1946 році.

Одночасткова функція розподілу f1 x1 визначається так, що

V1 f1 x1 dx1

є імовірністю того, що фазові координати частинки,

209