Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4603 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Одесский национальный университет им. И.И. Мечникова
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Статы Экзамен / Статы / statukr

.pdf
Скачиваний:
80
Добавлен:
20.05.2015
Размер:
8.64 Mб
Скачать
☆

тенціал A магнітного поля, пов'язаний з H співвідношенням H rot A , вибрати у вигляді A 0, Hx, 0 , то стан електрона зручно характеризувати такими квантовими

числами:

n 0, 1, ... – осциляторне квантове число;

py ,

pz – проекції узагальненого імпульсу на осі

y , z ; 1 – спінове квантове число. Рівні енергії електрона із законом дисперсії (1.2) у магнітному полі дорів-

нюють:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n pz

 

1

 

 

p2

 

 

 

 

 

 

 

 

c n

 

 

 

z

BH,

(5.38)

 

 

 

 

 

2

2m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

де

B

 

 

e

 

2mc

– магнетон Бора. Перші два доданки в пра-

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

вій частині (5.38) пов'язані з орбітальним рухом електрона, а останній являє собою енергію спінового магнітного моменту електрона в магнітному полі. Рівні енергії вироджені

з кратністю S

2 l 2

, де S – площа перетину зразка, у яко-

 

 

 

 

 

 

 

 

му знаходяться електрони, площиною x, y , а l

c

 

e

 

H

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

– мінімальний «радіус» електронної орбіти в магнітному полі (магнітна довжина). Виродження пов'язане з тим, що енергія (5.38) не залежить від положення орбіти на площиніx, y . З'ясуємо, як магнітне поле впливає на термодина-

мічні функції ідеального електронного газу.

5.6.1. Густина електронних станів у магнітному полі

Для розрахунку термодинамічних величин електронного газу необхідно знати густину станів. Вона може бути отримана з формули (1.17). У розглянутому випадку одноелект-

160

де

ронна густина станів дорівнює:

 

 

 

 

 

 

n

p

z

,

(5.39)

 

 

 

 

 

 

 

npy pz

– густина станів з орієнтацією спіну . Що стосується суми за py , то вона дорівнює кратності виродження рівнів (5.38):

 

 

 

 

 

 

1

 

S

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 l

2

 

 

 

 

 

 

 

 

 

 

py

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

У результаті сума (5.39) набуває вигляду:

 

 

 

V

 

 

 

 

 

 

1

 

p2

 

 

 

 

 

 

 

 

c n

 

 

 

 

 

z

 

BH dpz . (5.40)

 

 

 

2

 

 

 

2m

 

2 l

 

n

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тут ми скористалися правилом (5.6) переходу від підсумовування за pz до інтегрування:

 

L

 

dpz ,

2

pz

 

 

V SL – об’єм газу. У виразі (5.40) використовуємо відому властивість -функції:

x 1 x .

Тоді парціальна густина станів (5.40) становиться рівною:

 

2mV

 

 

 

 

 

 

dpz

2

2

 

(5.41)

 

 

2 l

2

pn pz

,

 

 

n

 

 

 

 

де

p2 2m ,

n n

161

 

 

1

 

 

 

n

c n

 

 

BH

(5.42)

2

 

 

 

 

 

– рівні Ландау. Інтеграл (5.41) відмінний від нуля лише в тому випадку, коли n . Це означає, що верхня межа

в сумі дорівнює деякому цілому числу

n . Воно

n

 

дорівнює цілій частині кореня рівняння n . Викорис-

товуючи в (5.41) формулу для -функції складного аргументу

x

 

 

x xi

 

 

 

 

 

 

 

xi

 

 

 

 

i

 

 

( xi – корені рівняння x 0 , штрихом позначена похідна функції x за аргументом), одержуємо:

m

3

 

c

n

 

1

 

 

 

 

2

 

 

 

 

 

 

 

V

 

 

 

 

 

 

 

 

 

 

.

(5.43)

 

 

2 2

 

 

 

 

 

 

 

 

 

 

 

2

 

n 0

 

n

 

 

 

 

 

 

 

 

 

 

 

Графік цієї функції показаний на рис. 5.7.

Рис. 5.7. Густина електронних станів у магнітному полі

Парціальна густина станів (5.43) має кореневі особливості

162

на рівнях Ландау (5.42). У випадку

H 0 сума за n

 

 

c

 

 

у (5.43) може бути замінена інтегралом

 

dn . У резуль-

 

 

0

таті вираз (5.43) переходить у густину електронних станів (1.20) за відсутності магнітного поля.

5.6.2. Великий потенціал електронного газу в магнітному полі

Роль індексу i , який характеризує одноелектронні стани

в магнітному

 

полі, відіграють

квантові

числа

Ландау:

i n, py , pz ,

. Тому великий потенціал (5.1) дорівнює:

 

1

 

 

 

 

 

p

 

1

 

 

 

 

ln 1 e

 

n

 

z ,

 

 

.

(5.44)

 

 

kT

 

np

y

p

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

 

 

Оскільки квантові числа входять тільки в енергію електрона, вираз (5.44) може бути записаний у вигляді:

 

1

 

 

 

 

 

d ln 1 e

,

(5.45)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

де – густина станів (5.39), (5.43). Виконаємо у формулі (5.45) інтегрування за частинами. Для цього покладемо

d , d

де – число станів електрона з енергією, яка не пере-

вищує . Воно дорівнює:

d .

0

163

Тут врахований той факт, що нижня межа спектра енергії електрона (5.38) у випадку вільних електронів дорівнює:

0 1

c

BH 0 .

2

 

 

Нижче цієї межі станів Ландау немає. У результаті інтегрування одержуємо:

 

1

ln 1 e

 

 

 

 

 

 

 

 

d f , (5.46)

 

0

 

 

 

0

 

 

 

 

де f – функція розподілу Фермі (5.2). Позаінтегральні

члени в (5.46) зникають на верхній межі за рахунок логарифма, а на нижній

0 0 .

(5.47)

Покладемо

 

 

d

 

 

d

 

 

 

і знову виконаємо в (5.46) інтегрування

за частинами.

З огляду на

 

 

0 0 ,

 

 

знаходимо

 

 

 

 

 

 

 

df

 

 

d

 

 

.

 

0

 

 

d

 

 

 

 

(5.48)

(5.49)

У підрозділі 1.2 було показано, що густина станів може бути записана у вигляді контурного інтеграла:

 

1

a i

d z e ,

 

 

(5.50)

2 i

 

a i

 

 

 

 

 

 

164

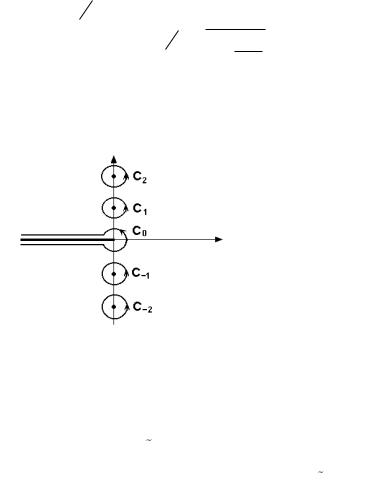
де z – одночастинкова статсума. Постійна a вибрана так, щоб усі особливості функції z були розташовані

ліворуч контура інтегрування в площині комплексної змінної ( рис. 5.8).

Рис. 5.8. Контур інтегрування в інтегралі (5.50)

Одночастинкова статсума дорівнює:

 

 

 

 

n

 

z

 

 

S

 

L

 

z

npy pz

exp

 

 

p

 

 

 

2 l2

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dpz exp

n

 

 

 

 

 

 

 

 

 

 

 

1

 

 

p

2

 

 

 

z

 

 

c n

 

 

 

 

BH

(5.51)

2

2m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 m 3 2

 

 

c

 

2

V

 

 

2

 

ch BH.

 

 

 

 

 

 

 

 

 

2

3

 

 

 

 

c

 

 

 

sh

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

У граничному

випадку H 0 одержуємо звідси відомий

вираз (4.12). Формули (4.12) і (5.51) відрізняються лише тим, що в (4.12) опущена двійка, яка враховує дві орієнтації

спіну

електрона, а

в (5.51)

– комплексна

змінна

a i Im .

 

 

 

 

Із

(5.50) і

(5.51)

видно, що

підінтегральна

функція

в (5.50) має точку розгалуження 0 і полюси першого

165

порядку в точках

 

 

 

l 2 il

1

l 1, 2,... ,

(5.52)

 

c

 

 

 

які є нулями гіперболічного синуса. У площині проведе-

мо розріз між точками і 0 уздовж дійсної осі. З огляду на (5.47) і (5.48), із формули (5.50) одержуємо:

 

1

 

a i d

 

z e ,

 

 

 

 

 

 

2 i

 

 

 

 

 

a i

 

 

 

 

 

 

 

 

 

 

(5.53)

 

1

 

a i

 

d

z e .

 

 

 

2 i

 

2

 

 

a i

 

 

 

 

 

 

 

 

 

 

 

При інтегруванні функції (5.50) з’являються інтеграли

a i

d

z

n 1, 2 ,

 

 

(5.54)

n

a i

 

 

 

 

 

 

 

які дорівнюють нулю, тому що контур інтегрування в (5.54) можна замкнути в правій напівплощині, де підінтегральна функція не має особливостей. Із (5.50) і (5.51) видно також, що густина станів дорівнює нулю нижче межі суцільного спектра 0 1 . Дійсно, при 0 1 контур інтегрування

в (5.50) доповнюємо півколом великого радіуса в правій напівплощині, де підінтегральна функція не має особливостей. Оскільки інтеграл за півколом прямує до нуля, коли

його радіус зростає, одержуємо 0 1 0 .

Після підстановки (5.53) і z (5.51) у формулу

(5.49), одержуємо для великого потенціалу електронів вираз:

166

 

 

 

 

 

 

 

df

 

 

 

 

d

 

 

 

,

 

 

 

 

 

 

 

d

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

де

 

 

 

 

 

 

 

 

 

 

 

V 2 m 32 c a i

d

 

e

 

 

 

 

 

 

 

 

3

 

 

 

 

5

 

 

2 2 i

a i

 

2

 

 

 

(5.56)

 

 

 

 

 

 

 

 

 

 

(5.55)

ch B H . sh c

2

Контур інтегрування на рис. 5.8 деформуємо так, як показано на рис. 5.9.

Рис. 5.9. Деформація контуру інтегрування в інтегралі (5.56)

Розріз обходить петлю C0 , а точки l (5.52) обходяться по

колах Cl l 1,

2, ... малого радіуса.

Відповідно до

цього великий потенціал (5.55) дорівнює:

 

 

0 ,

(5.57)

де 0 – внесок за рахунок інтегрування за петлею C0 , а

– за рахунок інтегрування за колами Cl .

За відсутності магнітного поля з формули (5.56) одержуємо:

167

 

0

2

V 2 m

32

 

d

e

 

.

(5.58)

 

2

3

 

 

 

7

 

 

 

 

 

 

2 i C

 

2

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

Після заміни змінної інтегрування u інтеграл у (5.58)

зводиться до відомого представлення Ханкеля для -функ- ції Ейлера:

 

 

 

 

 

u

 

1

 

1

 

du

e

.

(5.59)

z

2 i

z

 

C0

 

u

 

 

 

 

 

 

 

 

Використовуючи це представлення, з (5.58) одержуємо:

0 V 42m32 5 2, 15 2 3

 

 

 

 

 

 

 

 

 

 

7

 

 

15

 

де враховано

 

 

 

 

 

 

. При нульовій температурі

 

 

 

 

 

2

 

 

8

 

 

похідна від функції Фермі в (5.55) дорівнює -функції:

 

df

 

0 ,

 

(5.60)

d

 

 

 

 

 

 

 

 

 

 

 

 

де 0 F – хімічний

потенціал електронів

(5.11) при

T 0 . У результаті при T 0

 

і H 0 знаходимо:

0 V

 

 

 

 

32

 

 

 

 

4

 

2m

5

2.

(5.61)

 

 

 

 

 

0

 

 

 

15 2 3

 

 

 

 

 

 

 

 

З огляду на формулу (2.94), з (5.11) і (5.61) одержуємо відомий вираз (5.14) для тиску електронного газу.

5.6.3. Парамагнетизм Паулі і діамагнетизм Ландау

У слабкому магнітному

полі

можна

скористатися

розкладом ch BH і

sh

c

у

ряди

за ступенями

 

2

 

 

 

 

 

 

168

аргументів. Обмежуючись у цих розкладах квадратичними за H членами, одержуємо:

 

 

 

0 V

2 m 32 c

 

 

d e

 

 

0

2

3 2 i

 

5

 

 

c

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C0

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

(5.62)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

1

 

c

 

2

 

 

 

 

 

 

 

 

 

 

 

2

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

BH

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

6

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Перший доданок у правій частині (5.62) дає внесок (5.61) у потенціал за відсутності магнітного поля. Доданок

з B2 H2 обумовлений спіном електронів і дає внесок у парамагнітну сприйнятливість електронного газу. Доданок ізc 2 обумовлений орбітальним рухом електронів. Він дає

внесок у діамагнітну сприйнятливість. У випадку вільних електронів із законом дисперсії (1.2) відношення величини першого доданка в квадратних дужках (5.62) до величини другого дорівнює 3. Таким чином, парамагнітна сприйнятливість вільного електронного газу в три рази перевищує діамагнітну сприйнятливість. Парамагнітна сприйнятливість обчислена вперше В. Паулі (1927), а діамагнітна – Л. Д. Ландау (1930).

Для обчислення інтегралів (5.62) знову використовуємо представлення -функції (5.59). У результаті внесок електронних спінів у функцію (5.62) дорівнює:

P

V 2

 

m 32 e2 2H2

 

 

 

 

.

 

 

 

0

2

2 3 m2c2

 

 

 

 

 

 

 

Внесок орбітального руху має вигляд:

169

Соседние файлы в папке Статы
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности