Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4603 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Одесский национальный университет им. И.И. Мечникова
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

Статы Экзамен / Статы / statukr

.pdf
Скачиваний:
80
Добавлен:
20.05.2015
Размер:
8.64 Mб
Скачать
☆

навмання вибраної із системи, лежать в елементі об’ємом dx1 d 3r1d 3 p1

її фазового простору. Вона задовольняє умову нормування

 

 

1

 

dx1 f1 x1 1

 

 

 

 

 

 

 

 

V

 

 

 

 

 

 

 

і пов'язана з функцією fN очевидним співвідношенням

 

1

f1 x1 dx2...dxN fN x1, x2 ,..., xN .

(6.1)

V

 

 

 

 

 

Прикладом одночасткової функції розподілу є наведена в підрозділі 4.1 функція розподілу Максвелла. В ідеальному рівноважному газі імовірність знайти частинку в еле-

менті об’єму d 3r1d 3 p1 дорівнює:

f1 p1 d 3 p1 d 3r1 , V

де f1 p1 – максвеллівська функція розподілу (4.3), нормована умовою (4.1).

Двочасткова функція розподілу f 2

визначена так, що

 

1

f

 

x , x

dx dx

(6.2)

 

 

2

V 2

1

2

1

2

 

 

 

 

 

 

 

є імовірністю знайти одну частинку в елементі об’ємом dx1 , а іншу – в об’ємі dx2 . Ця функція нормована умовою

 

 

 

 

 

 

1

 

 

 

 

 

 

(6.3)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx1dx2 f2 x1, x2 1.

 

 

Вона пов'язана з

fN співвідношенням:

 

 

 

 

1

f

 

x , x

 

 

 

dx ...dx

f

x , x , x ,..., x

 

.

(6.4)

V 2

 

 

 

 

2

1 2

 

 

3

N N

1 2 3

N

 

 

 

 

 

 

 

 

 

 

 

210

З'ясуємо, яка структура f 2 в однорідній ізотропній системі.

Оскільки система рівноважна, для

fN можна використа-

ти канонічний розподіл Гіббса:

 

 

 

 

 

 

H X

 

 

fN X Ae

kT

,

(6.5)

 

 

 

де H X – гамільтонова функція системи,

A – нормуваль-

на константа. Гамільтонова функція дорівнює:

H q, p K p U q ,

(6.6)

де K p – кінетична енергія системи ( p – набір узагальнених імпульсів частинок), U q – потенціальна енергія взає-

модії частинок між собою, яка залежить від їх узагальнених координат q . Тоді, інтегруючи функцію (6.5) за x3,..., xN ,

одержуємо:

f2 r1, p1, r2 , p2 f1 p1 f1 p2

 

r1 r2

 

.

(6.7)

 

 

Функція називається радіальною функцією розподілу. Із (6.2) випливає, що

12 r1 r2 d 3r1d 3r2

V

є імовірністю того, що одна частинка системи перебуває в об’ємі d 3r1 , а друга – в об’ємі d 3r2 . Функція нормова-

на умовою

V12 d 3r1d 3r2 r1 r2 1.

Переходячи тут до інтегрування за r1 r2 і r2 , одержуємо

211

 

1

 

d 3r r 1.

(6.8)

V

 

 

 

 

Задача обчислення f 2

звелася до розрахунку

радіальної

функції розподілу.

Ясно тепер, що s -часткова функція розподілу f s пов'я- зана з N -частковою співвідношенням:

V s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

f

 

x ,..., x

 

dx

 

...dx

 

f

 

x ,..., x , x

,..., x

 

.

 

 

s

 

 

N

N

N

 

 

 

1

s

 

 

 

s 1

 

 

 

1

s s 1

 

 

Умова нормування для неї має вигляд:

 

 

 

 

 

 

 

 

 

 

1

 

 

dx1...dxs fs 1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Звідси видно, що

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

f

 

dx ...dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

s

 

 

 

 

 

 

 

 

 

 

 

V s

 

1

 

 

s

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

є імовірністю

перебування

частинок

1,..., s в

елементах

об’ємом dx1,..., dxs .

6.2.Зв'язок термодинамічних величин з одночастковою

ідвочастковою функціями розподілу

У цьому курсі теоретичної фізики ми маємо справу в основному з величинами двох типів – адитивними і бінарними. Прикладом адитивної величини є кінетична енергія системи:

N

2

 

K p

pa

.

 

a 1

2m

Відповідно до формули (1.26), її середнє значення дорівнює:

212

 

 

dX fN X K p N dX fN

X

p12

 

K

2m

 

 

 

 

 

 

 

 

(6.9)

 

 

 

 

 

 

 

 

 

 

 

 

 

p12

N

 

 

 

p12

N dx1

 

dx2...dxN fN X

 

 

dx1

 

f1 x1 .

2m

V

 

2m

Звідси видно, що для обчислення середнього значення адитивної величини достатньо знати одночасткову функцію розподілу.

Прикладом бінарної величини є енергія парної взаємодії частинок між собою:

 

 

 

 

 

U uab ,

(6.10)

де uab u

 

 

 

 

a b

 

 

ra rb

 

– потенціальна енергія

взаємодії двох

 

 

частинок, які перебувають у точках ra і rb . Ми припуска-

ємо, що вона залежить лише від відстані між частинками. Середнє значення потенціальної енергії (6.10) дорівнює:

U dX fN X U dXfN X u12 u13 ... u N 1 N . (6.11)

Оскільки функція fN не змінюється при перестановці її аргументів, інтеграли в (6.11) відрізняються лише позна-

ченням

змінних

інтегрування.

Іншими словами, усі

N N 1

 

 

 

 

пари частинок дають однаковий внесок в інте-

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

грал (6.11). Тому

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N N 1

dXfN X u12

 

 

U

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

N N 1

dx1dx2 u12 dx3...dxN fN X

(6.12)

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

N N 1

dx dx u f

 

x , x .

 

 

 

 

2

 

 

 

 

 

 

 

 

2V 2

 

 

1

2

12

1

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

213

Таким чином, для розрахунку середніх значень бінарних величин необхідно знати двочасткову функцію розподілу.

З огляду на (4.1) і (6.7), представимо вираз (6.12) у вигляді

 

 

 

1

Nn d 3ru r r ,

 

U

(6.13)

2

 

 

 

 

 

де n NV – густина газу. Тут ми поклали N 1 N , тому що N 1. В інтегралі (6.12) знову використані змінні інтегрування r1 r2 та r2 . У результаті внутрішня енергія

неідеального газу дорівнює:

 

 

3

 

1

 

 

 

 

 

 

E H N

 

kT

 

n d 3ru r r .

(6.14)

 

 

 

 

 

2

 

2

 

 

Щоб обчислити її, необхідно конкретизувати енергію взаємодії частинок u r і знайти радіальну функцію розподілу.

Для цього скористаємося формулою (3.14) для вільної енергії:

 

dqdp

 

 

H q, p

 

F kT ln Z kT ln

e

kT

.

 

 

 

 

h

3N

 

 

 

 

 

N !

 

 

 

Підставляючи сюди вираз (6.6), одержуємо

Z Z0 Q ,

де Z0 – знайдений раніше статінтеграл ідеального газу

(4.13), а

 

1

 

 

U q

 

Q

dqe

kT

(6.15)

 

 

 

V

N

 

 

 

 

 

 

 

 

– конфігураційний інтеграл. У результаті вільна енергія набуває вигляду:

F F0 Fвз ,

214

де F0 збігається з вільною енергією ідеального газу (4.14), а

Fвз kT ln Q

(6.16)

– внесок взаємодії.

Щоб обчислити (6.16), замінимо потенціальну енергію

U на U ,

де 0 1 . В остаточному виразі

для Fвз

покладемо 1. У результаті

 

 

 

 

 

 

 

 

 

1

 

 

 

U q

 

 

 

 

Q

 

 

 

 

 

 

V N

dqe

 

kT

,

 

(6.17)

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

Fвз kT ln Q 1

kT d

 

ln Q .

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

Підставляючи сюди (6.17) і виконуючи диференціювання за , знаходимо

1 d

Fвз U , (6.18)

0

де

 

 

 

 

U

 

 

 

 

dq Ue kT

U

 

.

U

 

 

 

 

dqe kT

Із формули (6.13) одержуємо:

U 12 Nn d 3r u r r ,

де r – радіальна функція розподілу для системи частинок з потенціальною енергією u r . У результаті внесок (6.18) у вільну енергію набуває вигляду:

215

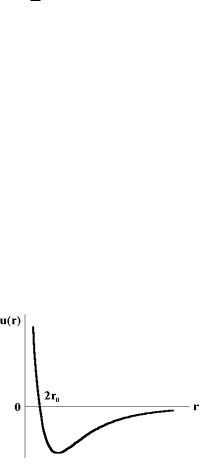
1

Fвз 12 Nn d d 3ru r r . (6.19)

0

Вважаючи тут d 3r 4 r2dr , знаходимо:

1

 

 

Fвз 2 Nn d drr2 u r r .

(6.20)

0

0

 

Проблема обчислення внеску (6.20) міжчастинкової взаємодії у вільну енергію системи звелася до обчислення радіальної функції розподілу.

6.3. Рівняння Ван-дер-Ваальса

Потенціальна енергія взаємодії двох нейтральних атомів u r як функція відстані між ними схематично показана на рис. 6.1.

Рис. 6.1. Енергія міжатомної взаємодії

При зближенні атомів їх електронні оболонки відштовхуються. При збільшенні відстані між ними відштовхування змінюється слабким вандерваальсівським притяганням. Відстань між атомами, при якій потенціальна енергія стає рівною нулю, ми позначили 2r0 . Відомо, що ця відстань

216

порядку радіуса потенціалу міжчастинкової взаємодії. Вона дорівнює декільком ангстремам.

Щоб обчислити внесок взаємодії частинок у вільну енергію (6.20), необхідно знати радіальну функцію розподілу. Обчислимо її для розрідженого газу. Будемо вважати, що

середня відстань між частинками n

1

3 велика в порівнянні

 

з радіусом r0 міжчастинкової взаємодії:

nr3 1.

 

(6.21)

0

 

 

Використаємо розклад радіальної функції розподілу r

у ряд за ступенями малого параметра (6.21). Із формули (6.20) видно, що для обчислення внеску взаємодії у вільну енергію в першому порядку теорії збурень за параметром (6.21) необхідно знайти r у нульовому порядку.

Із формул (6.4)–(6.7) випливає, що радіальна функція розподілу r1 r2 може бути отримана шляхом інтегру-

вання канонічного розподілу Гіббса (6.5) за імпульсами усіх частинок і за координатами усіх частинок, крім першої і другої:

 

 

r1 r2

 

Дe u12 d 3r3... d 3rN

(6.22)

 

 

exp u13 u23 ... u N 1 N

,

 

 

 

 

 

 

 

 

 

 

 

 

де Д – нормувальна

стала,

– зворотна температура.

Потенціальна енергія

взаємодії

частинок

(6.10) записана

у вигляді:

 

 

 

U u12

u13

u 23

... u1k ...

(6.23)

u k 1 k ... u1N ... u N 1 N .

 

217

Конфігураційний інтеграл (6.15) можна одержати шляхом інтегрування (6.22) за r1 і r2 . В інтегралі

d 3rN exp u1N ... u N 1 N

(6.24)

 

 

 

 

 

 

 

 

введемо функції

 

 

 

ik

exp uik 1.

 

(6.25)

Тоді цей інтеграл представляється у вигляді:

 

d 3r

 

 

N 1

 

 

 

 

1

 

 

iN

... .

(6.26)

N

 

 

 

 

 

 

 

 

i 1

 

 

 

 

У дужках ми обмежилися лінійними за iN членами. У ви-

падку газу малої густини інші члени можна опустити. Дійсно, функція (6.25) помітно відмінна від нуля всередині кулі радіусом r0 . Це означає, що помітний внесок в інтеграл

d 3rN iN kN

ми одержимо в тому випадку, коли вектори ri , rk , rN пере-

бувають усередині цієї кулі. Однак перебування трьох частинок усередині сфери взаємодії в розрідженому газі – подія малоімовірна. Обмежуючись у (6.26) лише лінійними за iN членами, одержуємо наближене значення інтеграла

(6.24):

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3r

 

 

 

N 1

 

V 2 N 1 B ,

 

 

 

 

 

d

1

 

 

 

 

(6.27)

 

 

 

 

N

 

 

 

iN

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i 1

 

 

 

 

 

 

 

 

 

де

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

u r

 

 

 

 

 

u r

 

B

d

3

 

e

2 drr

2

e

 

 

 

 

r

1

 

 

 

 

 

1

 

 

(6.28)

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

218

– другий віріальний коефіцієнт. Оскільки він порядку r03 , відношення другого доданка в (6.27) до першого пропор-

ційне малому параметру

(6.21).

Підставляючи

(6.27)

у (6.22), одержуємо:

 

 

 

 

r Дe u r

N

V 2

k 1 B .

(6.29)

 

 

 

 

 

k 3

 

 

У цьому наближенні конфігураційний інтеграл (6.15) дорівнює:

 

1

N

k 1 B .

Q

V 2

 

V N

 

 

k 1

 

 

 

 

Із формули (6.29) видно, що в нульовому наближенні за параметром (6.21) радіальна функція розподілу дорівнює:

r Ce u r .

Константу C знаходимо з умови нормування (6.8):

1

C

 

 

d 3re u r

C

 

d 3r 1 r C .

 

 

V

 

V

 

 

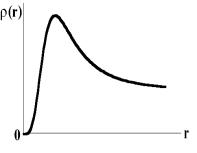
Графік функції

 

 

 

 

 

 

 

 

 

 

r e u r

(6.30)

схематично показаний на рис. 6.2.

Рис. 6.2. Радіальна функція розподілу (6.30)

219

Соседние файлы в папке Статы
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности