
Статы Экзамен / Статы / statukr
.pdfвеличина E T0S P0V зменшується і у стані повної рівно-
ваги досягає мінімуму. Насправді йшлося лише про зменшення цієї величини, а в тому, що вона досягає мінімуму, необхідно переконатися. Іншими словами, необхідно переконатися в стійкості стану рівноваги, про яке йшлося у підрозділах 2.1, 2.7. Зокрема, обмежуючись у підрозділі 2.1 першими похідними від ентропії, ми довели лише її екстремальність. Переконаємося в тому, що в стані рівноваги вона дійсно максимальна або величина E T0S P0V
мінімальна. Для цього необхідно дослідити знак других похідних від термодинамічних величин.
Нехай тіло самодовільно, без зовнішнього об'єкта роботиR 0 , виходить зі стану рівноваги із середовищем. Тоді
E T0 S P0 V 0 , |
(2.67) |
де E , S , V – відхилення енергії, ентропії й об'єму тіла
від їхніх значень у стані повної рівноваги. При цьому будемо припускати, що тіло саме по собі залишається рівноважним, тобто число його термодинамічних ступенів свободи дорівнює двом. Будемо характеризувати макростан тіла його ентропією та об'ємом. Розкладемо E у ряд
Тейлора за малими відхиленнями S , |
V : |
|
||||||||||||||||||
|
|
|
E |
|
|
|
|
E |
|
|
|
|
|
|
|
2 |
|
|
||
E |
|
|
|
S |
|
|
V |
1 |
|
|
E |
S 2 |
||||||||
S |
|
V |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
S 2 |
|
|||||||||
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.68) |
||||
|
2 E |
|
|
|
|
2 E |
|
|
|
|
|
|
|
|||||||
|
|
V |
2 |
|
|
|
||||||||||||||
2 |
|
|
|
|
S V |
|
|
|
|
|
|
... |
|
|||||||
|
|
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|||
|
S V 0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||
У цьому розкладі ми обмежилися членами другого порядку малості за S , V . Індексом нуль відмічені величини, які
стосуються стану рівноваги тіла із середовищем. З огляду на (2.3), (2.7) і підставляючи розклад (2.68) у (2.67),
91
знаходимо: |
|
|
|
|
|
|
|
|
||
|
2E |
|
S 2 |
2 |
2E |
S V |
2E |
V 2 |
0 , |
(2.69) |
|
S 2 |
S V |
|
|||||||
|
|
|
|
V 2 |
|
|
||||
де індекс нуль у рівноважних величин опущений. Квадратична форма (2.69) змінних S , V буде позитивно визна-
ченою в тому випадку, коли
2 E |
|
2 E |
|
|
2 E 2 E |
|
2 E 2 |
|
|||||||
|
|
0, |
|
|
0 |
, |
|
|
|
|
|
|
|
|
0 . (2.70) |
|
2 |
|
2 |
|
2 |
|
|
2 |
|
||||||
S |
|
V |
|
|
S |
|
V |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
S V |
|
|||||
Перетворимо ці нерівності.
З формул (2.3) і (2.33) випливає, що
|
2E |
|
T |
|
T |
|
||
|
|
2 |
|
|
|
|
|
. |
|
|
|||||||
|
S |
|
S V |
|
CV |
|
||
|
|
|
|
|
||||
|
|
|
V |
|
|
|
|
|
Вимагаючи позитивність цієї величини, знаходимо першу термодинамічну нерівність:
|
|
|
|
CV 0 . |
(2.71) |
||||
Аналогічно з |
|
|
|
|
|
|
|
|
|
|
2E |
|
|
|
P |
|
|||
|
|
2 |
|
|
|
|
0 |
||
|
|
||||||||
|
V |
|
|
|
V S |
|
|||
|
|
S |
|
||||||
одержуємо другу нерівність |
|
|
|
|
|||||
|
|
|
|
P |
|
0 . |
(2.72) |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||||
|
|
|
|
V S |
|
|
|
||
Вона означає, що адіабатична стисливість (2.31) позитивна. Ліву частину третьої нерівності (2.70) можна записати
у вигляді якобіана:
92
|
|
|
|
|
E |
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
, |
|
|
|
|
T , P |
|
|
|
|
||||
|
|
|
|
|
|
V |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||||||
|
|
|
|
S,V |
S,V |
|
|
|
|
||||||||||
Переходячи тут до змінних T , V , одержуємо: |
|
||||||||||||||||||
|
|
|
T , P |
|
|
P |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T , P |
|
T ,V |
|
|
|
|
|
|
|
P |
|
|||||||
|
|
|
|
V |
|
|
T |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
0 . |
S,V |
S,V |
S |
|
|
|
||||||||||||||
|
|
|
|
CV |
V |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
T ,V |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
З урахуванням (2.71) знаходимо звідси третю термодинамічну нерівність:
|
P |
0 . |
(2.73) |
|
|
|
|
||
|
||||
|
V |
|
|
|
|
|
T |
|
|
Іншими словами, ізотермічна стисливість (2.53) позитивна. З формули (2.52) і нерівності (2.73) випливає, що різниця теплоємностей CP CV позитивна, тобто
CP CV 0 . |
(2.74) |
Нерівності (2.71)–(2.74) забезпечують стійкість стану рівноваги термодинамічної системи. Якщо в деякому стані вони не виконуються, тіло як однорідна рівноважна система в цьому стані перебувати не може.
Навіть якщо система однорідна, нерівності (2.71)–(2.74) ще не гарантують її абсолютну стійкість. Вони отримані при нескінченно малому відхиленні параметрів системи від їхніх рівноважних значень. Рядом з мінімумом величини E T0S P0V може перебувати більш глибокий мінімум.
У такому випадку початковий стан рівноваги називається метастабільним. При досить великому відхиленні термодинамічних величин від їхніх значень у метастабільному
93
стані система може вже не повернутися в цей стан. Через деякий час вона перейде з метастабільного стану в стан
знайбільш глибоким мінімумом величини E T0S P0V .
2.9.Теорема Нернста
Уцьому підрозділі ми розглянемо поведінку ряду термо-
динамічних величин поблизу абсолютного нуля температури T 0 .
З формули (2.25) і нерівності (2.71) зрозуміло, що при зменшенні температури при постійному об'ємі внутрішня
енергія рівноважного тіла зменшується. Її значення E0 при
T 0 називається енергією основного стану. Нагадаємо, що стан системи при T 0 називається основним, а стани при T 0 – збудженими. Аналогічно, з (2.35) і (2.74) випливає, що теплова функція при T 0 і постійному тиску зменшується. Її значення при нульовій температурі позначимо W0 .
Будемо розглядати ентропію тіла як функцію температури і деякого параметра а, який характеризує його макростан. У ролі а найчастіше виступають або об'єм тіла, або тиск. Із формул (2.23) і (2.24), а також нерівностей (2.71) і (2.74) видно, що при зменшенні температури при постійному а ентропія системи зменшується. Однак зробити висновок про її значення при нульовій температурі на підставі лише першого і другого принципів термодинаміки неможливо. Постулюється, що
lim |
S T , a1 S T , a2 |
0 . |
(2.75) |
T 0 |
|
|
|
Це означає, що при T 0 відстань між кривими |
S T , |
||
отриманими при різних значеннях а, прямує до нуля. Вважається також, що всі ці криві сходяться на початку координат (рис. 2.3):
94
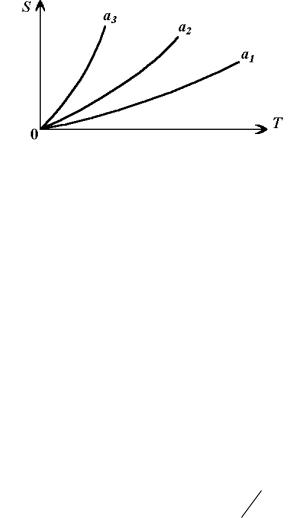
lim S 0 . |
(2.76) |
T 0 |
|
Рис. 2.3. Залежність ентропії від температури
Це твердження називається третім принципом термодинаміки, або теоремою Нернста (1906).
Якщо в співвідношенні (2.75) a1 і a2 відрізняються нескінченно мало, воно може бути переписане у вигляді:
|
|
|
|
|
S |
0 . |
|
(2.77) |
|
|
|
|
|
lim |
|
|
|||
|
|
|
T 0 |
a |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
Зокрема, |
|
|
|
|
|
|
|
|
|
|
|
S |
0 |
|
|
S |
0 . |
|
|
lim |
|
|
|
, |
lim |
|
(2.78) |
||
|
|||||||||
T 0 |
V |
|
|
T 0 |
P |
|
|
||
|
|
|
T |
|
|
T |
|
|
|
Третій принцип термодинаміки часто формулюють як принцип недосяжності абсолютного нуля. Припустимо, що тіло може існувати при температурі T 0 . Використовуємо його як холодильник в оборотному циклі Карно. Тоді зміна ентропії робочого тіла в процесі ізотермічного розширення
при температурі нагрівача T дорівнює S Q T , де Q –
теплота, передана тілу від нагрівача. На адіабатах ентропія тіла не змінюється. Не змінюється вона і на ізотермі T 0 , тому що ця ізотерма, згідно з (2.76), є одночасно і ізоентро-
95
пою. Зміна ентропії S робочого тіла в результаті здійснення ним оборотного циклу Карно виявилася обмеженою. Це суперечить другому принципу термодинаміки. Отже, передумова про досяжність абсолютного нуля неправильна.
Твердження (2.76) означає, що статистична вага основного стану рівноважної системи дорівнює одиниці. Іншими словами, основний стан може бути реалізовано єдиним способом.
Третій принцип термодинаміки дозволяє знаходити постійні при інтегруванні термодинамічних співвідношень. Так, з формул (2.23) і (2.24) з урахуванням (2.76) випливає, що
T |
|
|
CV |
V ,T |
|
T |
CP P,T |
|
S V ,T dT |
|
, |
S P,T dT |
. (2.79) |
||||
|
|
T |
T |
|||||
0 |
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
||
Для збігу цих інтегралів необхідно, щоб |
|
|
||||||
|
|
lim CV 0 , |
lim CP 0 . |
|
(2.80) |
|||
|
T 0 |
|
|
T 0 |
|
|
||
З'ясуємо, як поводиться коефіцієнт теплового розширення тіла
|
1 |
|
V |
(2.81) |
|
|
|
||
|
||||
|
V |
|
T P |
|
при T 0 . Використовуючи співвідношення Максвелла (2.46) і рівність (2.78), одержуємо
lim lim |
1 |
|
S |
0 . |
|
|
|
|
|||
|
|||||
T 0 |
T 0 V |
|
P |
|
|
|
|
|
|
T |
|
Аналогічно знаходимо межу термічного коефіцієнта тиску
|
1 |
|
P |
(2.82) |
|
|
|
||
|
||||
|
P |
T |
|
|
|
|
|
V |
|
96
при T 0 :
lim |
1 |
|
S |
0 . |
|
|
|
|
|
||
|
|
||||
T 0 |
P |
V |
|
||
|
|
|
|
T |
|
Інтегруючи рівність (2.35) при постійному тиску, маємо:
T
W W0 dTCP .
0
Отже, потенціал Гіббса як функція Р і Т може бути записаний у вигляді:
T |
T |
CP P,T |
|
|
P,T W TS W0 dTCP P,T T dT |
. |
|||
T |
||||
0 |
0 |
|
||
|
|
|||
Для обчислення необхідно |
знати W0 |
і функцію |
||
CP P,T по всій області температур.
2.10. Залежність термодинамічних величин від числа частинок
До цього моменту ми вважали, що число частинок у системі не змінюється при різних процесах, що відбуваються в ній. Тим часом часто доводиться мати справу із системами зі змінним числом частинок. Такі системи називаються відкритими. Прикладом відкритої системи є фаза речовини, яка перебуває в рівновазі з іншими фазами. У процесі фазового перетворення число частинок
укожній фазі змінюється. Якщо частинки тіла вступають
ухімічну реакцію, число частинок даного елемента також змінюється. Тому термодинамічні величини відкритої системи залежать вже не від двох параметрів, як у попередніх підрозділах, а від трьох. У ролі третьої макровеличини
97
виступає середнє число частинок N у системі. З'ясуємо, як різні величини залежать від N.
Величини, які фігурують у термодинаміці, можна розділити на дві групи – інтенсивні та екстенсивні (адитивні) величини. Інтенсивні величини постійні вздовж однорідної рівноважної системи і не залежать від числа частинок в ній. Прикладами таких величин є температура, тиск, питомі термодинамічні потенціали. Екстенсивні величини зростають пропорційно числу частинок у системі при незмінних інтенсивних величинах. Екстенсивними є об’єм, число частинок, ентропія, термодинамічні потенціали системи.
Якщо адитивні аргументи термодинамічної величини змінюються в кілька разів, а інтенсивні величини при цьому незмінні, адитивна термодинамічна величина змінюється у стільки ж разів. З цього визначення випливає, що
P,T , kN k P,T , N ,
де k – деяке число. Підбираючи k так, щоб kN 1, одержуємо:
P,T , N N P,T ,1 N P,T , |
(2.83) |
|
де |
|
|
|
|
(2.84) |
N |
||
– потенціал Гіббса в розрахунку на одну частинку. Він називається хімічним потенціалом. Адитивність внутрішньої енергії означає, що
E kV , kS, kN kE V , S, N ,
звідки випливає:
E V , S, N Ne , s ,
98

де e E N – внутрішня енергія в розрахунку на частинку,
V N і s S N – питомі об’єм і ентропія. Аналогічно знаходимо:
W S, P, N Nw s, P ,
F V ,T , N Nf ,T ,
де w W N і f F N – питомі теплова функція і вільна
енергія.
Із співвідношення (2.83) видно, що збільшення потенціалу Гіббса відкритої системи при постійних P і T дорівнює:
d P,T dN . |
(2.85) |
Воно зумовлене зміною числа частинок у системі і називається хімічною роботою. Ясно, що доданок (2.85) повинен бути врахованим у змінах (2.42) усіх термодинамічних
потенціалів, |
оскільки в процесі перетворення Лежандра |
|
в підрозділі |
2.3 змінні і N не використовувалися. |
|
У результаті: |
|
|
|
dE TdS PdV dN , |
|
|
dW TdS VdP dN , |
|
|
dF SdT PdV dN , |
(2.86) |
d SdT VdP dN .
Варто пам'ятати, що в співвідношеннях (2.86) хімічний потенціал (хімпотенціал) виражається через різні змінні. Наприклад, у виразі для dE він повинен бути вираженим через питомі ентропію та об’єм.
2.11. Хімічний потенціал
Хімічний потенціал системи визначається співвідношен-
99
ням (2.84). Усе, що говорилося про зміст потенціалу Гіббса в підрозділі 2.3, стосується і хімічного потенціалу. Із (2.86) видно, що він може бути отриманий шляхом диференціювання будь-якого термодинамічного потенціалу за числом частинок. При диференціюванні повинні залишатися постійними дві інші термодинамічні величини, які є природними змінними відповідного потенціалу:
|
E |
|
|
W |
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
. (2.87) |
|
N |
S ,V |
|
N |
S ,P |
|
N |
|
N |
|
|
|
|
|
|
T ,V |
|
T ,P |
|
У цих співвідношеннях хімпотенціал, як величина інтен-
сивна, |
виражається |
через |
пару інтенсивних величин – |
s, , |
s, P , T , |
і T , P |
відповідно. |
Одержимо термодинамічну тотожність для хімічного потенціалу. Для цього зміну потенціалу Гіббса (2.86) при-
рівнюємо до величини
d dN Nd .
Тоді одержуємо: |
|
d sdT dP . |
(2.88) |
Звідси видно, що хімпотенціал є термодинамічним потенціалом відносно змінних T, P. Знаючи цей потенціал, можемо одержати питому ентропію і питомий об’єм:
|
|
, |
|
|
(2.89) |
s P,T |
|
P,T |
. |
||
|
T |
P |
|
P |
|
|
|
|
T |
|
Одержимо умову рівноваги системи відносно обміну частинками між її частинами. Для цього в замкнутій системі виділимо дві частини 1 і 2, здатні обмінюватися частинками при незмінній енергії та об’ємі цих частин. Оскільки система замкнута, повне число частинок N N1 N2 у ній незмінне, тобто
dN2 dN1 .
100
