Статы Экзамен / Статы / statukr

термодинамічні величини. Іншими словами, статистична фізика є мікроскопічним обґрунтуванням термодинаміки.

Статистичну фізику часто називають статистичною механікою. Уже з назви зрозуміло, що цей розділ теоретичної фізики є синтезом механіки і теорії імовірностей. Якщо для опису руху частинок системи можна використовувати закони класичної механіки, ми будемо мати справу з класичною статистикою. Статистика, заснована на квантовій механіці, називається квантовою статистикою. У посібнику вони викладаються паралельно.

11

РОЗДІЛ 1. ОСНОВНІ ПРИНЦИПИ СТАТИСТИКИ

1.1. Мікроскопічний і макроскопічний стани системи

Теоретичне вивчення системи починається з опису моделі, яка лежить в основі теорії. Ми будемо розглядати замкнуту систему N точкових частинок, які взаємодіють між собою. При цьому ми відсторонюємось від внутрішніх ступенів свободи частинок, а закон їх взаємодії поки що не конкретизуємо.

Центральним питанням теорії є питання про спосіб задання стану системи. Згадаємо, як він задається в класичній механіці та у квантовій теорії.

Мікроскопічний стан системи частинок у класичній

pa – її імпульс. Тоді набір величин ra , pa , де a 1,..., N , задає

мікростан системи в класичній механіці. частинок та імпульси залежать від часу t : ra

залежність може бути знайдена з рівнянь Ньютона:

В аналітичній механіці мікростан системи задається набором узагальнених координат q q1,..., qr і швидкос-

тей q q1,..., qr або імпульсів p p1,..., pr , де r 3N – число ступенів свободи системи. Якщо відомий мікростан q 0 , q 0 системи в початковий момент часу, то її стан

12

у будь-який інший момент може бути отриманий з рівнянь Лагранжа:

де L L q, q – функція Лагранжа системи.

У статистичній механіці частіше використовується метод Гамільтона. У цьому методі мікростан системи задається набором узагальнених координат q та імпульсів

p . Імпульс pi , спряжений координаті qi , визначається співвідношенням:

pi L .

qi

Залежність мікростану від часу q t , p t можна одержати, розв’язуючи систему рівнянь Гамільтона:

у фазовому просторі. Цей простір має 2r вимірів. На осях декартової системи координат, введеної в ньому, будемо відкладати координати та імпульси

частинок системи. Оскільки частинки рухаються, фазова точка переміщається у фазовому просторі, описуючи фазову траєкторію. Елемент об’єму у фазовому просторі дорівнює:

13

r

d dqdp dqidpi .

i 1

Об’єм області у фазовому просторі зображується інтегралом

dqdp

по цій області.

Розглянемо побудову фазової траєкторії системи на

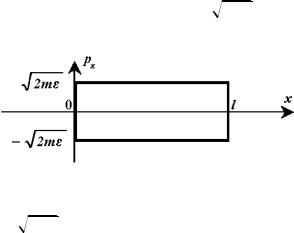
Тут – енергія частинки, p – її імпульс, m – маса частинки. Нехай частинка здійснює одновимірний рух у нескінченно глибокій потенціальній ямі, тобто рухається уздовж осі x між паралельними дзеркальними стінками в точках x 0, x l, які пружно відбивають частинку. Її фазовий

простір двовимірний. Оскільки між стінками частинка рухається вільно з імпульсом p 2m , її фазовою траєкторією є контур прямокутника на рис. 1.1.

Рис. 1.1. Фазова траєкторія частинки

Тут px 2m – проекція імпульсу частинки на вісь x . Площа, обмежена фазовою траєкторією, дорівнює:

14

Із збільшенням енергії вона збільшується пропорційно

12 .

Після відкриття хвильових властивостей частинок стало зрозумілим, що зображувати мікростан квантової системи точкою у фазовому просторі не можна. Для однієї частинки існують співвідношення невизначеностей Гейзенберга:

де x,..., px ,... – невизначеності координат і компонент

імпульсу частинки, h – стала Планка. Згідно з цими співвідношеннями величини x і px, наприклад, не можуть мати одночасно певних значень, тому не можна використовувати фазовий простір для зображення станів квантової системи.

Мікростан квантової системи зображується хвильовою функцією або повним набором фізичних величин n .

Відомо, що динамічні змінні F q, p класичної механіки у квантовій теорії зіставляються з лінійними ермітовими

операторами ˆ . У повний набір фізичних величин входять

F

власні значення повного набору операторів, які відповідають цим величинам. Ці оператори незалежні і взаємно комутують. Їх кількість дорівнює числу ступенів свободи системи. Наприклад, повний набір для однієї частинки утворюють координати x, y, z або компоненти імпульсу

px , py , pz . Якщо частинка перебуває в центральному полі,

її мікростан зручно зображувати головним, орбітальним і магнітним квантовими числами.

Еволюція квантової системи за часом описується рівнянням Шредингера:

15

ˆ

iH ,

t

стала, i – уявна одиниця. Це рівняння дозволяє одержати стан у момент t, t , якщо відомий стан 0 у почат-

ковий момент і між цими моментами не здійснювались вимірювання системи.

Наприклад, розглянемо стаціонарні стани частинки, яка виконує одновимірний рух у нескінченно глибокій потенціальній ямі. Вони нумеруються квантовим числом n 1, 2,... ,

яке характеризує мікростан частинки. У стані n на ширині ями l укладається ціле число напівхвиль де Бройля:

де n 1, 2,...

Мікростан квантової системи, заданий хвильовою функцією або повним набором фізичних величин, назива-

16

ється чистим станом. У випадку макросистеми в цей набір входить велика кількість змінних. Одержати їх у реальному експерименті практично неможливо, тому повний набір n або стан не відомі. Відомо лише, що система може

перебувати у різних станах 1, 2 ,..., i ,... з імовірностями

таким способом, називається змішаним станом. Поняття про змішані стани введене І. фон Нейманом у 1927 році.

У термодинаміці стан макроскопічної системи задається інакше. Для характеристики стану використовуються величини, які стосуються системи в цілому або її макроскопічних частин. Прикладами таких величин є об’єм системи V, її енергія E, ентропія S, температура T, тиск P та інші. Ці величини називаються макроскопічними, а стан, заданий за допомогою цих величин, – макроскопічним станом.

При макроскопічному описі системи виникає питання про число незалежних величин, необхідних для задання макростану, і про вибір цих величин. Ми будемо розглядати, в основному, прості системи типу газу, для характеристики макростану яких досить двох незалежних величин. Якщо система перебуває в зовнішньому полі, до них необхідно додати величини ( 1, 2 ,...) , які характери-

зують зв'язок системи з полем. Це можуть бути, наприклад, компоненти вектора напруженості електричного поля, у якому перебуває система заряджених частинок. Кількість незалежних величин, необхідних для задання макростану, називається числом термодинамічних ступенів свободи системи.

Вибір незалежних величин, які задають макростан системи, залежить від того, як система виділяється з ото-

17

чення, тобто від типу контакту досліджуваної системи із середовищем. Розглянемо чотири типові випадки.

Замкнутою називається система з фіксованими об’ємом V, числом частинок N і енергією E. Її макростан задається двома незалежними величинами – V і E. Інші величини можуть бути виражені через V і E.

Досліджувана система, як правило, перебуває в середовищі з великим числом ступенів свободи. Його часто називають термостатом. Якщо система обмінюється з середовищем лише енергією, її макростан задається об’ємом і температурою. У рівновазі температура системи збігається з температурою термостата.

Часто доводиться мати справу з відкритими системами, які обмінюються з середовищем енергією і частинками. Макростан таких систем характеризується трьома незалежними величинами – об’ємом V, температурою T і хімічним потенціалом .

Якщо система перебуває в циліндрі під поршнем і обмінюється з середовищем енергією, її об’єм уже не фіксований. Її макростан задається температурою T і тиском P. Останній збігається із тиском у середовищі. Макроскопічні величини, згадані тут, будуть введені в другому розділі цього посібника.

Ясно, що фіксація макроскопічного стану системи не визначає однозначно її мікроскопічний стан. Наприклад, знаючи об’єм і енергію газу, ми не можемо вказати положення його фазової точки у просторі або значення величин, які входять у повний набір n. Даному макростану буде відповідати множина положень фазової точки, багато значень величин n. Виникає питання про число мікростанів, які відповідають даному макростану. Щоб відповісти на нього, необхідно навчитися підраховувати мікростани.

1.2. Число станів і густина станів

18

1.2.1. Число станів і статистична вага

Нехай E – число мікростанів системи з енергією, яка

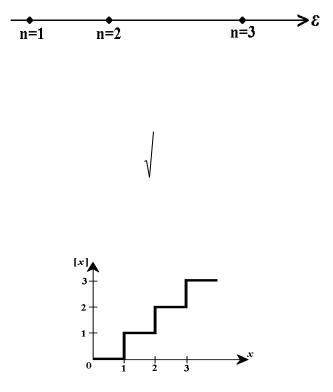
не перевищує заданого значення E . Обчислимо це число для однієї частинки, яка виконує одновимірний рух у нескінченно глибокій потенціальній ямі. Її рівні енергії задаються формулою (1.5). Схематично такий спектр енергії показаний на рис. 1.2. Точками на осі відзначені дозволені значення енергії частинки.

Рис. 1.2. Енергетичний спектр частинки

Задаючи деякі значення енергії , ми легко знайдемо число станів (точок на осі ) з енергією, меншою або рівною :

рис. 1.3.

Рис. 1.3. Ціла частина x

Вираз можна переписати у вигляді

19

nm

1.

n 1

Очевидним узагальненням цієї формули для будь-якої квантової системи є вираз

Тут En – рівні енергії системи. Їх можна знайти з рівняння Шредингера:

ˆ

H n En n ,

де n – власна функція гамільтоніана системи H . Значком

позначене підсумовування за мікростанами системи,

En E

енергія яких не перевищує E . Можна позбутися обмеження En E і перейти до підсумовування за всіма n, якщо

ввести функцію Хевісайда:

сичному випадку. У цьому випадку відносна різниця між числом і його цілою частиною невелика. Тому приблизно одержуємо

20