
Статы Экзамен / Статы / statukr
.pdf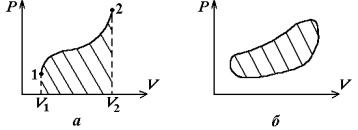
2 |
2 |
dE TdS PdV |
|
1 |
1 |
між двома станами 1 і 2 не залежить від шляху, який з'єднує ці стани, а інтеграл за замкнутим контуром у площині параметрів стану дорівнює нулю. Такі ж властивості має і ентропія системи. Робота і теплота цих властивостей не мають. Це видно вже з того, що функції стану T V , S
й P V , S у співвідношеннях (2.17) залежать від двох змін-
них. У результаті інтеграли від (2.17) між двома станами залежать від процесу, тобто від шляху, який з'єднує ці стани. Тому ми використовуємо позначення Q і R для
кількості теплоти і роботи. Сказане означає, що можна говорити про енергію стану, але не можна говорити про кількість теплоти і роботи в даному стані. Внутрішню енергію не можна розділити на теплову і механічну. Це можна зробити лише для нескінченно малих величин, які фігурують у (2.8).
Якщо макростан системи зображується точкою на площині V , P , а квазістатичний процес – суцільною лінією,
то робота, яку виконує система при переході із стану 1 у стан 2, дорівнює площі фігури, заштрихованій на рисунку
2.1 (а):
Рис. 2.1. Робота системи: а – при переході 1 2; б – при циклічному процесі
71
V2 |
|
|
A1 2 |
PdV . |
(2.22) |
V1 |
|
|
Якщо процес циклічний, робота дорівнює площі, заштрихованій на рис. 2.1 (б).
Теплоємність системи
C Q dT
також залежить від процесу нагрівання. Ми будемо мати справу в основному з теплоємністю при постійному об’ємі:
C |
|
S |
T |
|
|
V |
|
|
|
|
T V |
і з теплоємністю при постійному тиску:
C |
|
|
S |
P |
T |
. |
|
|
|
|
|
|
|
|
T P |
Із (2.8) випливає, що |
|
|
|
|
|
E |
, |
C |
|
||
V |
|
|
|
|
|
T V |
|
(2.23)
(2.24)
(2.25)
де внутрішня енергія виражена через об’єм і температуру. Ми припускали, що макростан системи характеризується
двома параметрами. У загальному випадку таких параметрів більше. Наприклад, у випадку системи в заданому зовнішньому полі до величин, які характеризують макростан, необхідно додати компоненти напруженості поля1, 2 ,..., k . Рівні енергії En і функція розподілу n у (2.11)
залежать від цих величин. У результаті робота R , виконана над системою, обумовлена не тільки зміною об’єму, але і параметрів 1,..., k :
72
|
k |
|
|
R PdV i d i , |
(2.26) |
|
i 1 |
|
де i |
– функції стану, які залежать від V , S, . |
Робота |
i d i повинна бути врахована у співвідношенні (2.8):
i
dE TdS PdV i d i . |
(2.27) |
i |
|
Як приклад нагадаємо відомий з електродинаміки вираз для роботи, затраченої на зміну вектора індукції в одиниці об'єму речовини:
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
R dD |
HdB |
, |
|
|
|
|
(2.28) |
||
|
|
|
|
|
|
|
|
|||||
|
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де |
і |
H – напруженості електричного і магнітного полів, |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
і |
B – |
вектори електричної |
|
і |
магнітної |
індукції |
|||||
в речовині. |
Тут роль параметрів |
|
відіграють компоненти |
|||||||||
|
|
|
|
|
– |
|
|
|
|
|
||
векторів D і B , а функцій стану |
|
4 |
і |
H |
4 |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
||
2.3. Термодинамічні потенціали
Співвідношення (2.8) і (2.27) нагадують формулу для зміни потенціальної енергії частинки в потенціальному
полі при переміщенні dr :
dUFdr ,
де F – сила, яка діє на частинку. З цієї причини внутрішню енергію системи називають термодинамічним потенціалом, або характеристичною функцією змінних S,V , . Ці змінні
аналогічні координатам частинки. Величини T , P, нази-
ваються термодинамічними силами. Ясно, що внутрішню енергію можна виразити через іншу пару змінних, наприк-
73
лад V ,T , і написати відповідний диференціал. Чому ж ми
називаємо внутрішню енергію термодинамічним потенціалом стосовно змінних S,V , ? Справа в тому, що у спів-
відношення (2.27) при 0 входять п'ять функцій стану: E,T, S, P,V . Дві з них можна вибрати за незалежні змінні.
Тоді для визначення трьох величин, які залишилися, необхідно мати три рівняння. Цими рівняннями можуть бути (2.27), а також
PP V ,T
–термічне рівняння стану системи і
EE V ,T
–калоричне рівняння стану. При цьому за незалежні змінні ми вибрали V і T. Якщо ж незалежними змінними вважати S і V , то до співвідношення (2.27) необхідно додати лише
одне рівняння |
|
|
E E V , S . |
|
|
|
|
|
|
|
|
|
(2.29) |
||
Тоді T і P можуть бути визначені диференціюванням цієї |
|||||||
функції: |
|
|
|
|
|
|
|
|
E V , S |
, |
|
E V , S |
(2.30) |
||
T V , S |
|
|
P V , S |
|
. |
||
|
S |
|
|
|
V |
|
|
|
V |
|
S |
|
|||
Ці міркування показують, чому у (2.8) ентропії і об’єму як незалежним змінним ми надаємо перевагу. Вони є природними змінними функції стану E .
Знаючи функцію (2.29), ми можемо одержати інші термодинамічні величини шляхом диференціювання. Зокрема, теплоємність (2.23) дорівнює:
|
|
S |
|
C |
T |
|
|
|
|||
V |
|
|
|
|
|
T V |
|
|
|
|
T |
|
|||
|
|
|
|
|
|
||
|
|
2 |
E |
|
|||
|
|||||||
|
|
|
|||||
|
|
|
|
||||
|
|
S |
2 |
|
|||
|
|
|
V |
||||
|
|
E |
|
|
|||
|
|
|
|
|
|
|
|
|
|
S |
|
|
|||
|
|
V |
. |
||||
|
|
2 |
|
|
|
||
|
|
E |
|
||||
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
S |
|
V |
|
|||
74
Величина, обернена адіабатичній стисливості:
|
|
|
1 |
|
V |
|
|
K |
S |
|
|
|
|
, |
(2.31) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
V |
|
P S |
|
|
дорівнює |
|
|
|
|
|
|
|
|
1 |
|
P |
|
|
2E |
|||
|
|
V |
|
V |
|
|
2 |
. |
|
|
|
|
|||||
|
KS |
V S |
|
|
V |
|
||
|
|
|
S |
|||||
Тут CV і KS виражені через змінні V |
і S . Нагадаємо, що |
|||||||
процес, який відбувається при постійній ентропії, називається адіабатичним.
Макростан простої системи можна задавати іншими парами термодинамічних величин: S, P , T ,V , T , P . Ці
змінні можуть виявитися зручнішими за змінні S,V .
Відповідно до цього, крім внутрішньої енергії, існують ще три термодинамічні потенціали щодо зазначених пар змінних. Розглянемо їх.
Щоб перейти від змінних S,V , які задають макростан системи, до змінних S, P, використаємо перетворення Лежандра. Розглянемо добуток V P і одержимо його збільшення при нескінченно малій квазістатичній зміні термодинамічних величин:
d VP VdP PdV .
Підставляючи PdV d VP VdP у (2.27), одержуємо:
d E PV TdS VdP. |
|
Це означає, що величина |
|
W E PV |
(2.32) |
є термодинамічним потенціалом щодо змінних |
S, P. Її |
називають тепловою функцією, або ентальпією. Збільшення ентальпії дорівнює:
75
dW S, P TdS VdP. |
(2.33) |
Видно, що dW має сенс кількості теплоти, яка передається системі в ізобаричному процесі. Із (2.33) знаходимо:
|
W |
, |
|
W |
(2.34) |
T S, P |
|
V S, P |
. |
||
|
|
|
|
|
|
|
S P |
|
|
P S |
|
Із (2.24) і (2.33) випливає, що теплоємність при постійному тиску може бути записана у вигляді:
C |
|
|
W |
, |
(2.35) |
P |
|
|
|||
|
|
|
|
|
|
|
|
|
T P |
|
|
де W повинна бути виражена через P і T . Для цього необхідно у W S, P підставити S P,T , знайдене з першо-
го співвідношення (2.34). |
|
Для переходу від змінних S,V до змінних T ,V |
знову |
скористаємося перетворенням Лежандра. Із |
|
d TS TdS SdT |
|
знаходимо TdS і підставляємо у (2.27): |
|
d E TS SdT PdV . |
|
Величина |
|
F E TS |
(2.36) |
є термодинамічним потенціалом щодо змінних V ,T. Вона |
|
називається вільною енергією. Її приріст дорівнює |
|
dF SdT PdV . |
(2.37) |
Звідси видно, що зменшення вільної енергії при ізотермічному процесі дорівнює роботі системи над навколишніми тілами. Із (2.37) знаходимо
|
F |
, |
S V ,T |
|
|
|
|
|
|
T V |
|
|
F |
(2.38) |
P V ,T |
. |
|
|
|
|
|
V T |
|
76
Якщо функція F F V ,T відома, то друге співвідношення
(2.38) дозволяє одержати рівняння стану системи простим диференціюванням.
Виразимо внутрішню енергію як функцію змінних V ,T
через вільну енергію: |
|
|
|
|
|
|
|
|
F |
|
|
|
F |
|
|
E F TS F T |
|
T 2 |
|
|
|
. |
(2.39) |
|
|
||||||
|
|
|
|
|
|
|
|
|
T V |
|
T T V |
|
|||
Щоб одержати термодинамічний потенціал щодо змін- |
|
них P,T , підставимо PdV d VP VdP у (2.37): |
|
d F PV SdT VdP. |
|
Величина |
|
P,T F PV E TS PV W TS |
(2.40) |
називається термодинамічним потенціалом Гіббса. Його приріст дорівнює:
d SdT VdP. |
(2.41) |
Оскільки у правій частині (2.41) немає звичних понять роботи і теплоти, для з'ясування фізичного змісту збільшення потенціалу Гіббса можна звернутися до термодинамічної тотожності (2.27). Оскільки змінні , до цього
часу не використовувалися при перетворенні Лежандра, робота i d i залишається у всіх співвідношеннях (2.27),
i
(2.33), (2.37) і (2.41):
dE TdS PdV i d i ,
i
dW TdS VdP i d i ,
i
(2.42)
dF SdT PdV i d i ,
i
d SdT VdP i d i .
i
77
Необхідно тільки пам'ятати, що величини i щораз
виражаються через інші змінні. Наприклад, у формулі для dF вони повинні бути виражені через V ,T , .
Із (2.42) видно, що збільшення потенціалу Гіббса дорівнює роботі над системою при зміні параметрів , якщо тільки температура і тиск постійні.
Із (2.41) випливає, що
|
|
, |
|
|
(2.43) |
S T , P |
|
V P,T |
. |
||
|
T |
P |
|
P |
|
|
|
|
T |
|
Маючи T , P , із другої рівності (2.43) можна одержати рівняння стану тіла у вигляді V V P,T .
Теплова функція може бути виражена через потенціал Гіббса за допомогою співвідношень (2.40) і (2.43):
|
|
T 2 |
|
|
|
W TS T |
|
|
|
. |
|
|
|||||
|
T P |
|
|
T T P |
|
Це співвідношення дає теплову функцію як функцію змінних P,T .
З тотожностей (2.42) видно, що зміни всіх термодинамічних потенціалів, обумовлені змінами величин , є однаковими, якщо тільки кожну з цих змін розглядати при відповідній парі постійних величин:
E S,V |
W S,P F T ,V |
P,T |
id i . (2.44) |
|
|
|
i |
Це твердження називається теоремою про малі добавки. Далі вона буде неодноразово використана.
Легко переконатися в тім, що знання одного з термодинамічних потенціалів дозволяє знайти інші потенціали як функції їх природних змінних. Тоді легко можуть бути знайдені їхні перші похідні (2.30), (2.34), (2.38), (2.43) та інші термодинамічні величини. У наступному підрозділі ми побачимо, як це робиться.
78

2.4. Перетворення похідних від термодинамічних величин
Покажемо, як, знаючи рівняння стану тіла P P V ,T
і його теплоємність, обчислити похідні одних термодинамічних величин за іншими.
Одержимо |
похідну |
|
|
CV V ,T |
|
|
|
, |
якщо |
рівняння |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
стану |
задане у |
|
|
вигляді |
|
P P V ,T . |
Використовуючи |
|||||||||||||||||||||||||||
визначення (2.23), знаходимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
C |
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
2S |
|
|
|
||||||||||||
|
|
|
V |
|
|
|
|
|
|
T |
|
|
|
|
|
|
T |
|
|
|
|
|
. |
|
||||||||||
|
V |
|
|
|
V |
|
T |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V T |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
Підставляючи сюди |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
T |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
одержуємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
3F |
|
|
|
|
|
|
|
3F |
|
|
|
|
|||||||
|
|
|
|
V |
|
|
T |
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|||||||||||
|
V |
|
|
V T 2 |
|
T |
2 V |
|
||||||||||||||||||||||||||
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
F |
|
|
|
|
|
|
|
2 P |
|
|
|
|
|
|
|||||||||||
|
|
T |
|
|
|
|
|
V |
|
|
|
|
T |
|
|
|
. |
|
|
|
|
|||||||||||||
|
T 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T 2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
V |
|
|
|
|
|
|
V |
|
|
|
|
||||||
В останній рівності враховано вираз для тиску (2.38). |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
||
Для обчислення похідної |
|
|
S |
|
|
|
за рівнянням стану |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
P P V ,T необхідно врахувати (2.38). Тоді |
|
|
|
|
||||||||||||||||||||||||||||||
|
S |
|
|
|
2 F |
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
P |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(2.45) |
|||||||
|
|
V |
T |
|
|
V |
|
T |
||||||||||||||||||||||||||
|
V |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
V |
|
|
|
|
V |
|
|||
79
Це співвідношення можна одержати відразу, користуючись тим, що
dF SdT PdV
– повний диференціал. Аналогічно, з огляду на повні диференціали (2.27), (2.33) і (2.41), знаходимо
|
T |
|
|
P |
|
|
T |
|
|
V |
|
||
|
|
|
|
|
, |
|
|
|
|
|
, |
||
|
V |
S |
|
S |
|
|
P |
S |
|
S |
P |
||
|
|
|
|
V |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.46) |
|
|
|
|
S |
|
V |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
. |
|
|
|
||
|
|
|
|
P |
|
T |
P |
|
|
|
|||
|
|
|
|
|
T |
|
|
|
|
|
|
||
Рівності (2.45) і (2.46) називаються співвідношеннями Максвелла.
Із dE TdS PdV і співвідношення (2.45) знаходимо:
|
E |
|
S |
|
P |
|
|
|
|
T |
|
|
P T |
|
P . |
|
|||||||
|
V |
|
V |
|
T |
|
|
|
T |
|
|
T |
|
V |
|
Ця похідна легко обчислюється, якщо відоме рівняння стану P P V ,T .
Багато похідних легко перетворюються за допомогою якобіанів. Якобіаном переходу від пари змінних u, v до
пари x, y , пов'язаних рівняннями
u u x, y , |
v v x, y , |
називається детермінант
u,v |
|
u |
|
||
|
x |
|
x, y |
v |
|
|
|
x |
u |
|
|
|
(2.47) |
|
|
|
||
|
|
|
|
|
y |
|
u v |
|
u v . |
v |
|
x y |
|
y x |
y |
|
|
|
|
80
