
Статы Экзамен / Статы / statukr
.pdf
Оскільки в об’ємі немає ні джерел, ні стоків фазових точок, їх число змінюється лише за рахунок руху через поверхню , що обмежує об’єм . Число точок, які перетинають ділянку d цієї поверхні за одиницю часу, дорівнює:
uDd ,
де u q, p – швидкість «фазової рідини», а вектор d
спрямований уздовж зовнішньої нормалі до ділянки d . У результаті закон збереження числа фазових точок може бути записаний у вигляді:
d |
D |
d uD. |
(1.42) |
|
t |
|
|
|
|
Використовуючи теорему Гаусса
d uD d div uD
івважаючи об’єм нескінченно малим, можемо переписати закон збереження (1.42) у диференціальній формі:
D div uD 0. |
(1.43) |
|||
t |
|
|
|
|
Вхідна сюди дивергенція дорівнює: |
|
|
|
|
div uD Ddivu u D. |
||||
Якщо у виразі |
|
|
|
|
r |
qi |
pi |
|
|
divu |
|
|
||
|
|
|||
i 1 |
qi |
pi |
||
врахувати рівняння Гамільтона (1.1), то одержимо |
||||
divu 0. |
|
|
(1.44) |
|
41

Це означає, що розглянута тут «фазова рідина» нестислива.
Урезультаті рівняння (1.43) набуває вигляду
D u D 0.
t
Знову використовуючи рівняння (1.1), знаходимо
D |
D, H 0, |
(1.45) |
|||
t |
|
|
|
|
|
де |
|
|
|
|
|
r |
|
|
D |
|
|
D, H |
D H |
H |
|
||
|
|
||||
i 1 |
|
qi pi |
pi qi |
|
|
– дужки Пуассона для |
функції |
розподілу |
D q, p,t |
||
і гамільтонової функції H q, p,t . Остання явно залежить
від часу, якщо система перебуває в заданому змінному зовнішньому полі. Рівняння (1.45) називається рівнянням Ліувілля. Воно справедливе також і для функцій f і , які
відрізняються від D нормувальним множником:
t , H 0. (1.46)
Уквантовій статистиці роль функції розподілу відіграє статистичний оператор ˆ .
Щоб одержати рівняння для нього, необхідно в (1.46) здійснити заміни
|
|
|
|
, |
, H |
1 |
|
|
ˆ |
, |
|
|
|
|
|
|
|||||
|
|
|
|
|
, H |
|||||
|
|
|
|
ˆ |
|
i |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
де |
ˆ |
ˆ |
|
ˆ ˆ |
|
|
|
|
|
|
, H |
ˆ H H ˆ – комутатор операторів. Тоді одержу- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
ємо квантове рівняння Ліувілля:
42

|
|
i |
ˆ |
|
|
|
ˆ |
|
0. |
|
(1.47) |
||
|
|
|
|
|
|
||||||||
|
|
|
|
ˆ, H |
|
||||||||
|
|
|
t |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Повна похідна за часом |
|
|
|
|
|
|
|
|
|||||
|
d |
|
|
|
|
r |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
qi |
|
pi |
|||
|
dt |
t |
q |
|
|
p |
|||||||
|
|
|
|
|
|
i |
|
|
|||||
|
|
|
|
|
i 1 |
|
|
i |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
з урахуванням рівнянь (1.1) може бути записана у вигляді:
|
d |
|
|
|
||
|
|
|
t , H . |
|
||
|
dt |
|
||||
З огляду на (1.46), одержуємо звідси |
|
|||||
|
|
|
|
d |
|
|
|
|
|
|
|
0. |
(1.48) |
|
|
|
|
dt |
||
Це означає, що функція розподілу стала вздовж фазової
траєкторії. Якщо точка q, p у момент t |
перебуває на |
одній траєкторії з точкою q0 , p0 у момент |
t 0 , маємо: |
q, p,t q0 , p0 , 0 . |
(1.49) |
У момент t 0 виділимо у фазовому просторі системи нескінченно малий елемент об’єму d 0 і будемо стежити
за фазовими точками, що знаходяться усередині цього об’єму. У момент t вони будуть у деякому іншому об’ємі d . Їх число дорівнює:
D q0 , p0 ,0 d 0 D q, p,t d .
З огляду на рівність (1.49), отримуємо d d 0 ,
тобто виділена ділянка у фазовому просторі деформується, але її величина не змінюється (рис.1.6).
43
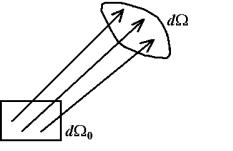
Рис. 1.6. Рух фазового об’єму
Це твердження справедливе і для скінченного об’єму
у фазовому просторі: |
|
|
d d 0. |
(1.50) |
|
|
0 |
|
Щоб переконатися в цьому, використаємо розв’язок рівнянь (1.1) q q q0 , p0 ,t , p p q0 , p0 ,t . Він однозначно пов'язує величини q, p і q0 , p0 . Переходячи в лівій частині рівності (1.50) до інтегрування за змінними q0 , p0 ,
одержуємо
d d 0 J ,
0
де
|
q, p |
|
|
q |
|
q |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
J |
|
|
q0 |
p0 |
|
|||
q0 |
, p0 |
|
p |
|
p |
|
||
|
|
|
|
|||||
|
|
q0 |
p0 |
|
||||
|
|
|
|
|
|
|||
– якобіан переходу. У початковий момент він дорівнює одиниці. Переконаємося в тому, що якобіан не залежить від часу:
44

dJdt 0.
Для цього скористаємося відомою властивістю якобіана:
|
|
|
|
|
|
q, p |
|
|
q, p |
|
|
q , p |
|
, |
|
|
(1.51) |
||||
|
|
|
|
|
|
q0 , p0 |
|
|
|
|
q0 , p0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
q , p |
|
|
|
|
|
|||||||||
|
|
|
– |
|
координати |
|
й імпульси |
частинок |
системи |
||||||||||||
де q , p |
|
|
|
||||||||||||||||||
в довільний |
момент t . |
Диференціюючи співвідношення |
|||||||||||||||||||
(1.51) за часом t при постійних t0 |
|
і t , одержуємо |
|
||||||||||||||||||
|
|
|
|
d |
|
q, p |
|
|
|
|
|
d |
q, p |
|
|
||||||
|
|
|
|
|
|
|
q , p |
. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
dt q0 , p0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
q0 , p0 dt q , p |
|
|
|||||||||||||
Після |
диференціювання |
|
покладемо |
t t . |
|
|
При |
цьому |
|||||||||||||
відмінні від нуля лише елементи детермінанта, розташовані на головній діагоналі:
|
d q, p |
|
|
|
|
|
q, p |
|
|
r |
q |
|
p |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
i |
. |
|
|
dt q |
|
, p |
|
q |
|
, p |
|
|
q |
p |
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
0 |
0 |
|
|
|
|
|
|
0 |
0 |
|
|
i 1 |
i |
|
|
i |
|
З огляду на (1.44), одержуємо |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
d |
|
q, p |
|
|
0, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
dt |
q , p |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
тобто якобіан J |
завжди дорівнює одиниці. |
Це доводить |
|||||||||||||||||||
інваріантність фазового об’єму (1.50).
Співвідношення (1.46), (1.48) і (1.50) є різними формулюваннями теореми Ліувілля. Якщо система рівноважна,
0 . Тоді рівняння (1.46) набуває вигляду:
t
, H 0.
45

У квантовій статистиці |
|
ˆ |
ˆ |
|
0 . Це означає, що функ- |
, H |
|||||
|
|
|
|
|
|
ція розподілу замкнутої системи є інтегралом рівнянь руху (1.1). Оскільки функція розподілу макросистеми, яка складається з незалежних частин, мультиплікативна, логарифм функції розподілу – це адитивний інтеграл руху. Але з механіки відомо лише сім однозначних адитивних інтегралів руху – енергія Е, три компоненти імпульсу
системи P і три компоненти кутового моменту M . Отже, ln – функція цих величин. Логарифм функції розподілу
підсистеми а повинен мати вигляд:
ln a a Ea Pa Ma , |
(1.52) |
де індексом а позначені величини, що стосуються підсистеми a, a , , , – сталі величини. Якщо підсистема
розглядається в системі координат, відносно якої вона як ціле нерухома, то з (1.52) випливає
ln a a Ea.
Це означає, що координати q, p квазізамкнутої підсистеми
входять у її функцію розподілу тільки через функцію Гамільтона:
H q, p . |
(1.53) |
На перший погляд здається, що проблема побудови явного вигляду функції розподілу макроскопічної системи зводиться до інтегрування рівняння Ліувілля (1.46) з належною початковою умовою. Однак розв’язати це рівняння так само важко, як і систему рівнянь Гамільтона. Тому побудова функції розподілу рівноважної системи вимагає додаткового постулату.
46

1.8. Мікроканонічний розподіл
Переходимо до побудови функції розподілу замкнутої рівноважної системи. Розглянемо спочатку класичну систему. Її макростан характеризується об’ємом V і енергією E . Насправді замкнутих систем не буває. Реальна система завжди взаємодіє з оточенням. Це приводить до того, що її енергія не фіксована точно, а лежить у деякому проміжкуE, E E . Іншими словами, фазова точка системи міс-
титься в тонкому шарі між двома гіперповерхнями постійної енергії у фазовому просторі системи: H q, p E
і H q, p E E . Припустимо, що функція розподілу
стала в межах цього шару. Фазова точка системи з рівною імовірністю може бути знайдена в будь-якій ділянці шару і не виходить за його межі:
q, p C, E H q,
0, E H q,
p E E, p E E.
Стала С може бути знайдена з умови нормування (1.22). Вона дорівнює:
C W1 ,
де W – статистична вага (1.12) макростану системи. Отже,
|
1 |
, E H q, p E E, |
|
|
|
|
|
|
|
||
q, p W |
|
(1.54) |
|
|
0, E H q, p E E. |
|
|
|
|
|
|
Такий розподіл називається мікроканонічним.
Поряд з функцією розподілу у фазовому просторі введемо функцію розподілу за енергією w E . Вона визначається так, що імовірність знайти енергію системи
47
в проміжку E, E dE дорівнює |
w E dE . Ця функція |
нормована умовою |
|
dEw E 1,
де інтегрування виконується за всією віссю енергії. Оскільки функція розподілу залежить лише від енергії системи,
легко виявити, що імовірність знайти фазову точку системи в проміжку dE дорівнює:
w E dE E d E ,
де d E – число мікростанів у проміжку dE . З огляду на
співвідношення d E dE , де E |
– густина станів, |
одержуємо |
|
w E E E . |
(1.55) |
Можна показати, що функція розподілу |
w F для будь- |
якої величини F q, p , що стосується системи, дорівнює
w F |
|
d |
q, p F F q, p . |
|||
|
|
|
||||
h3N N ! |
||||||
|
|
|
||||
З формул (1.15), (1.54) і (1.55) випливає, що у випадку квазізамкнутої системи і E E функція розподілу за енергією дорівнює
w E |
1 |
|
W |
|
1 |
|
E |
E |
|||
|
W |
|
|||
усередині проміжку і стає рівною нулю за його межами. У випадку E 0 строго замкнутої системи з енергією Е,
одержуємо
w H H E ,
де через H позначений аргумент функції w . Тоді у цьому
48
випадку з формули (1.55) одержуємо |
|
||||
q, p |
|
|
1 |
E H q, p . |
|
|
|
E |
|||
|
|
|
|
||
Як і очікувалось, функція розподілу стає нескінченною на гіперповерхні постійної енергії і дорівнює нулю за її межами.
Число мікростанів квантової системи в проміжкуE, E E дорівнює статистичній вазі W (1.12). Постулю-
ючи рівну імовірність для всіх цих станів, знаходимо функцію розподілу за станами:
|
|
1 |
|
|
En |
E E, |
||
n |
|
|
, |
E |
||||
|
||||||||
W |
|
|
|
|
(1.56) |
|||
|
|
0, |
|
E E |
|
або |
E E E. |
|
|
|
|
|
n |
|
|
n |
|
Її можна записати у вигляді: |
|
|
|
|
||||
|
n E,V |
|
E En |
, |
||||
|
|
|
||||||
|
|
|
|
|
|
W E,V |
||
де – функція, |
|
що |
фігурує |
в (1.13). Такий розподіл |
||||
у квантовій статистиці називається мікроканонічним. Йому відповідає мікроканонічний ансамбль.
Щоб одержати функцію розподілу за енергією wi для квантової системи, перепишемо статвагу у вигляді:
W |
gi , |
|
E Ei E E |
де підсумовування виконується за рівнями енергії, а gi – кратність виродження рівня Ei . Тоді імовірність того, що енергія системи дорівнює Ei , має вигляд відношення числа
49

станів з енергією Ei до повного числа станів у проміжку
E :
wi gi W .
1.9. Ентропія
Опис системи, прийнятий у класичній або квантовій механіці, є найбільш детальним. Якщо відоме положення фазової точки системи в її фазовому просторі або відома хвильова функція, ми маємо повну інформацію про систему. Перехід до менш детального опису, прийнятому в статистичній фізиці, супроводжується втратою інформації про стан системи. Мірою невизначеності в інформації є ентропія. Вона характеризує «ступінь розмазаності» макроскопічного стану системи за її можливими мікроскопічними станами, які достовірно не відомі.
Визначимо ентропію рівноважної квантової системи так, щоб вона була позитивною і адитивною. Ентропія системи повинна дорівнювати сумі ентропій її незалежних макрочастин. Зажадаємо, щоб у чистому стані, коли ми маємо повну інформацію про систему, ентропія дорівнювала нулю. У стані повної невизначеності, коли система з рівною імовірністю n перебуває в будь-якому можли-
вому мікростані n, ентропія повинна бути максимальною. Легко переконатися, що ці вимоги задовольняє гіббсівський вираз для ентропії:
|
|
|
|
ln . |
(1.57) |
||
Відповідно до формули (1.28), цей вираз дорівнює:
n ln n. |
(1.58) |
n |
|
Оскільки 0 n 1, ентропія позитивна: |
0 . Функція |
50
