Статы Экзамен / Статы / statukr

де t, s – пари проміжних змінних. Із (2.50) видно, що із

символами якобіана можна діяти як з чисельником і знаменником дробу.

Приведемо похідну T V S до вигляду, зручному для

обчислення за рівнянням стану і відомій теплоємності CV . Для цього записуємо цю похідну у вигляді якобіана:

Використовуючи властивість (2.50), знаходимо:

де враховане співвідношення Максвелла (2.45) і вираз для теплоємності CV (2.23).

Обчислимо різницю CP CV , маючи рівняння стану

81

у формі V V P,T . Для цього перетворимо теплоємність при постійному об’ємі:

Використовуючи властивість (2.50), легко знайти відношення адіабатичної стисливості (2.31) до ізотермічної стисливості

82

2.5. Максимальна робота. Цикл Карно

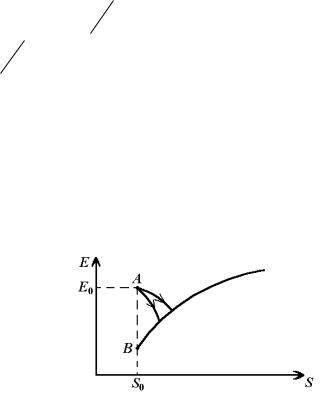
Розглянемо довільну теплоізольовану систему, яка перебуває в нерівноважному стані. Вона може складатися з декількох тіл, які не перебувають у тепловій рівновазі одне з одним. Нехай E0 і S0 – енергія та ентропія цієї системи.

Ці величини зіставимо з точкою A на діаграмі ентропія– енергія (рис. 2.2).

Рис. 2.2. До розрахунку максимальної роботи

Відповідно до нульового принципу термодинаміки, така система згодом переходить у стан рівноваги. Цей перехід

83

супроводжується зростанням її ентропії. Енергія рівноважної системи є функцією ентропії та об’єму: E E S,V .

Оскільки T E S V 0 , залежність E S при постійно-

му об’ємі зображується монотонно зростаючою кривою на рис. 2.2. Нерівноважна система може переходити з початкового стану A в кінцевий рівноважний стан різними шляхами. Два з них показані на рис. 2.2. Оскільки система теплоізольована, із закону збереження енергії (2.16) одержуємо для роботи системи над навколишніми тілами вираз:

Нас цікавить такий перехід нерівноважної системи у стан рівноваги, при якому її кінцевий об’єм дорівнює початковому. Такий перехід супроводжується виконанням роботи (2.54), обумовленої нерівноважністю системи, а не її розширенням. (При розширенні роботу (2.22) виконує і рівноважна система.) Із рис. 2.2 видно, що робота (2.54) буде максимальною в тому випадку, коли ентропія системи не змінюється, тобто перехід з початкового стану A у кінцевий на кривій E S відбувається шляхом AB . Такий пере-

хід є оборотним.

Визначимо максимальну роботу, яку можна одержати при обміні малою кількістю теплоти між двома тілами, що існують при температурах T1 і T2 . Нехай T2 T1 . Більш

гаряче тіло будемо називати нагрівачем, а більш холодне – холодильником. При стиканні тіл з різною температурою відбувається необоротний переніс тепла Q від нагрівача

до холодильника. Згідно з (2.17), ентропія системи при цьому зростає на величину

84

а робота не виконується. Щоб усунути кінцевий перепад температури при стиканні тіл, необхідно мати третє тіло, яке називається робочим тілом. Процес передачі теплоти від нагрівача до холодильника буде оборотним, якщо робоче тіло при температурі T2 стикається з нагрівачем,

одержує від нього кількість теплоти Q2 T2dS2 та, ізотер-

мічно розширюючись, виконує роботу. Потім робоче тіло адіабатично розширюється доти, поки його температура стане рівною T1 . Стикаючись з холодильником, робоче тіло

відбувається адіабатичний стиск робочого тіла до досягнення ним температури T2 . Такий замкнутий оборотний про-

цес називається циклом Карно. Якщо нагрівач і холодильник досить великі, їхні температури практично не змінюються, а робоче тіло повертається у вихідний стан. Зміни

Відношення виконаної роботи до отриманої від нагрівача кількості теплоти називають коефіцієнтом корисної дії (ККД) теплової машини, яка працює за циклом.

У випадку циклу Карно він дорівнює:

Звідси видно, що ККД 1 і не залежить від природи робочої речовини. ККД міг би дорівнювати одиниці

85

лише при T1 0 чи T2 , що неможливо. Отже, не можна

побудувати періодично діючу машину, яка виконувала б роботу тільки за рахунок тепла, отриманого від нагрівача, без передачі тепла холодильнику. Така машина називається вічним двигуном другого роду, а сформульоване вище твердження являє собою запропоноване Томсоном формулювання другого принципу термодинаміки. Є й інше формулювання другого принципу. Воно запропоноване Клаузіусом: самодовільний перехід тепла від менш нагрітого тіла до більш нагрітого неможливий.

2.6. Максимальна робота в середовищі. Нерівність Клаузіуса

Нехай нерівноважне тіло перебуває в рівноважному середовищі, температура T0 і тиск P0 якого незмінні. Інші

параметри середовища змінюються квазістатично. Середовище разом з тілом утворюють теплоізольовану систему. Вони можуть обмінюватися між собою енергією та об’є- мом, але не частинками. Крім того, існує механічний об'єкт, теплоізольований від тіла і середовища, здатний виконувати роботу над тілом. Об'єкт виконує над тілом роботу R , при цьому енергія, ентропія та об’єм тіла змінюються наE , S , V . З'ясуємо, при яких процесах робота R мінімальна і чому вона дорівнює. Через те що робота об'єкта над тілом відрізняється знаком від роботи тіла над об'єктом, можна говорити про максимальну роботу тіла над об'єктом.

Оскільки ентропія адитивна, середовище і тіло утворюють теплоізольовану систему, а ентропія механічного об'єк-

86

ності стосується оборотного процесу, а знак > – необоротного. Надалі величини, які стосуються середовища, відмічаємо індексом нуль, а величини без індексу стосуються тіла. Із закону збереження енергії (2.16) випливає

Через те що процеси в середовищі квазістатичні,

Тут зміни термодинамічних величин не передбачаються нескінченно малими. Врахуємо також сталість повного об'єму середовища і тіла:

Використовуючи (2.57)–(2.59), переходимо в нерівності (2.56) до величин, які стосуються тіла:

Це означає, що робота механічного об'єкта над тілом буде мінімальною, якщо процес зміни термодинамічних величин тіла оборотний. При цьому мінімальна робота дорівнює:

Розглянемо окремі випадки цієї формули.

Якщо тіло рівноважне, але не перебуває в рівновазі із середовищем, то зміна його внутрішньої енергії при нескінченно малій квазістатичній зміні ентропії та об'єму визначається формулою (2.8). Підставляючи цей вираз у (2.61), одержуємо:

У стані повної рівноваги між тілом і середовищем мінімальна робота (2.62) дорівнює нулю.

Нехай під впливом механічного об'єкта ентропія та об'єм

87

тіла не змінюються. Тоді з (2.61) одержуємо:

Rmin E

– мінімальна робота дорівнює зміні внутрішньої енергії тіла. Якщо процес відбувається так, що S 0 , а тиск P незмінний і дорівнює тиску в середовищі, то Rmin W .

а більшим числом величин. Тому сталість двох з них ще не означає, що ніякі процеси не відбуваються. У міру наближення системи до рівноваги число параметрів, необхідних для характеристики її стану, зменшується до числа термодинамічних ступенів свободи. Відбувається згадане в підрозділі 1.3 скорочення опису системи.

де Rmin – мінімальна робота, яку виконав би механічний об'єкт при заданій зміні параметрів E, S, V , яка від-

булася самодовільно. Із формули (2.63) видно, що нерівноважне тіло в процесі переходу в стан рівноваги із середовищем здатне виконувати позитивну роботу.

Через те що процеси в середовищі вважаються квазістатичними, то збільшення ентропії середовища в нерівності

(2.56) дорівнює S0 Q0 T0 , де Q0 – теплота, отримана

середовищем від тіла. Вона відрізняється від теплоти Q , отриманої тілом, лише знаком: Q0 Q . У результаті нерівність (2.56) набуває вигляду

88

Вона називається нерівністю Клаузіуса. Знак рівності стосується оборотної передачі тепла тілу при температурі T0 . Запишемо

S eS i S ,

де eS Q T0 – зміна ентропії тіла за рахунок переданого

йому ззовні тепла. Одержуємо з (2.64) нерівність:

i S 0 .

Тут i S – виробництво ентропії, зумовлене необоротними процесами всередині тіла. Знак eS може бути будь-яким, однак збільшення ентропії i S завжди позитивне.

2.7.Умови рівноваги

Упідрозділі 2.1 ми одержали дві умови рівноваги термодинамічної системи. Умовою рівноваги відносно обміну енергією між різними частинами системи є сталість її температури, а умовою рівноваги відносно обміну об'ємом

–сталість тиску. Одержимо умови рівноваги в термінах зміни термодинамічних потенціалів.

Із (2.60) випливає, що коли механічний об'єкт відсутній, а нерівноважне тіло переходить у стан рівноваги із середо-

вищем, величина E T0S P0V зменшується:

У стані повної рівноваги вона набуває мінімального значення.

Якщо в процесі переходу до стану рівноваги енергія та об'єм тіла не змінюються, тобто тіло являє собою замкнуту

89

систему, то з нерівності (2.65) одержуємо S 0 – закон зростання ентропії замкнутої системи. Якщо в процесі переходу в рівноважний стан S і V не змінюються, зменшується внутрішня енергія. У стані рівноваги вона міні-

потенціал Гіббса .

Щоб проілюструвати цей результат, розглянемо систему типу газу в циліндрі під рухливим поршнем. Нехай тиск і температура системи фіксовані і збігаються з тиском і температурою середовища. Об'єм системи не фіксований. Необхідна умова рівноваги може бути записана у вигляді:

зумовлена зміною об'єму при постійних Р і Т. ОскількиF V ,T PV , а Р і Т фіксовані,

звідки випливає відомий вираз (2.38) для тиску в рівноважній системі. У наступному підрозділі ми переконаємося в тому, що умова (2.66) дійсно відповідає мінімуму термодинамічного потенціалу.

2.8.Термодинамічні нерівності

Упопередньому підрозділі було показано, що при переході нерівноважного тіла в стан рівноваги із середовищем

90