
- •Министерство образования и науки украины
- •1.1.1. Крупномасштабные топографические съемки ……………...21
- •1.2.6.Проектирование площадки с соблюдением баланса
- •1.5.2.Классификация деформаций оснований зданий и
- •1.5.4.Геодезические знаки, используемые для измерений
- •1.5.6.Линейно-угловые построения для наблюдения за
- •2.1.5. Разбивка примыканий и пересечений автомобильных
- •2.1.8. Геодезические работы при гидротехнических
- •3.7.2.Расчет ошибок отдельных видов геодезических работ на
- •3.16.4.Определение правильности положения колец в плане
- •Введение предмет и задачи курса «инженерная геодезия»
- •Литература
- •1. Промышленное и гражданское строительство
- •1.1.Инженерные изыскания
- •1.1.1. Крупномасштабные топографические съемки
- •1.1.1.1.Номенклатура планов
- •1.1.1.2.Съемочная геодезическая сеть
- •1.1.1.3.Составление проекта теодолитных ходов
- •1.1.2.Городская полигонометрия и инженерно- геодезические сети
- •1.1.2.1.Общая характеристика сетей
- •1.1.2.2.Полигонометрические знаки
- •1.1.2.3.Передача координат на полигонометрические знаки
- •1.1.2.4.Измерение углов и длин при отсутствии видимости между точками
- •1.1.2.5. Метод редукции при линейных измерениях
- •1.1.3. Геодезические разбивочные опорные сети
- •1.1.4. Геодезическая строительная сетка
- •1.1.4.1. Назначение строительной сетки и ее точность
- •1.1.4.2. Проектирование строительной сетки
- •1.1.4.3. Способы детальной разбивки строительной сетки
- •1.1.4.3.1. Осевой способ
- •1.1.4.3.2. Способ редуцирования
- •1.1.4.4. Методы определения координат пунктов строительной сетки
- •1.1.4.5.Оценка точности построения строительной сетки
- •1.1.4.6. Контрольные измерения строительной сетки
- •1.1.4.7. Перевычисление координат
- •1.1.4.8. Определение высот пунктов строительной сетки
- •1.1.4.9. Методы построения сетей второго порядка
- •1.1.4.9.1.Полигонометрия
- •1.1.4.9.2. Метод четырехугольников без диагоналей
- •1.1.4.9.3. Микротриангуляция
- •1.1.4.9.4. Метод геодезических засечек
- •1.1.4.9.5. Микротрилатерация
- •1.1.4.9.6.Метод линейных геодезических засечек
- •1.2. Инженерно- геодезическое проектирование
- •1.2.1.Общие сведения о проектировании
- •1.2.2. Геодезическая подготовка для разбивки зданий способом перпендикуляров
- •1.2.3. Вынос на местность красных линий по заданным промерам от осей проезда
- •1.2.4. Вертикальная планировка площадки строительства методом проектных горизонталей
- •1.2.5.Составление проекта вертикальной планировки
- •1.2.6. Проектирование площадки с соблюдением баланса земляных работ
- •1.2.7. Подсчет объемов земляных работ
- •1.2.8. Проектирование наклонной плоскости без соблюдения баланса земляных работ
- •1.2.9. Условные обозначения, используемые при составлении проекта вертикальной планировки
- •1.3.1. Общие сведения о разбивочных работах
- •1.3.2. Способы разбивочных работ
- •1.3.3. Влияние исходных данных на точность плановой разбивки точек сооружений
- •1.3.4. Элементы разбивочных работ
- •1.3.5. Технология разбивочных работ
- •1.3.5.3.1. Общие сведения
- •1.3.5.3.2. Разбивка основных осей и их закрепление
- •1.3.5.3.3. Детальные геодезические разбивочные работы
- •1.2. Инженерно- геодезическое проектирование
- •1.2.1.Общие сведения о проектировании
- •1.2.2. Геодезическая подготовка для разбивки зданий способом перпендикуляров
- •1.2.3. Вынос на местность красных линий по заданным промерам от осей проезда
- •1.2.4. Вертикальная планировка площадки строительства методом проектных горизонталей
- •1.2.5.Составление проекта вертикальной планировки
- •1.2.6. Проектирование площадки с соблюдением баланса земляных работ
- •1.2.7. Подсчет объемов земляных работ
- •1.2.8. Проектирование наклонной плоскости без соблюдения баланса земляных работ
- •1.2.9. Условные обозначения, используемые при составлении проекта вертикальной планировки
- •1.3.1. Общие сведения о разбивочных работах
- •1.3.2. Способы разбивочных работ
- •1.3.3. Влияние исходных данных на точность плановой разбивки точек сооружений
- •1.3.4. Элементы разбивочных работ
- •1.3.5. Технология разбивочных работ
- •1.3.5.3.1. Общие сведения
- •1.3.5.3.2. Разбивка основных осей и их закрепление
- •1.3.5.3.3. Детальные геодезические разбивочные работы
- •1.4.1. Подземные коммуникации
- •1.4.2. Геодезические работы на нулевом цикле
- •1.4.2.1.1. Общие сведения
- •1.4.2.1.2. Возведение монолитных фундаментов
- •1.4.2.1.3. Устройство сборных железобетонных фундаментов
- •1.4.2.1.4. Свайные фундаменты
- •1.4.2.1.5. Фундаменты под колонны
- •1.4.2.1.6. Исполнительная съемка фундаментов
- •1.4.3. Геодезические работы при возведении наземной части зданий
- •А) Плановая разбивочная сеть на исходном горизонте
- •1.4.3.5.1. Контроль геометрических параметров сборных конструкций
- •Выверка конструкций
- •1.4.3.5.2. Монтаж и выверка колонн, исполнительная съемка колонн
- •Исполнительная съемка колонн
- •1.4.3.5.3. Монтаж и выверка панелей, исполнительная съемка панелей
- •1.4.3.5.4. Сборные железобетонные многоэтажные здания
- •Создание плановых сетей
- •Создание каркасных опорных и разбивочных сетей
- •1.4.3.5.5. Крупнопанельные и крупноблочные здания
- •Поэтажная геодезическая основа сборных высотных зданий
- •1.4.3.5.6. Каркасно-панельные здания
- •Технологическая увязка монтажных геодезических работ на этажах
- •1.4.4. Геодезические работы при монтаже оборудования
- •1.4.4.2. Выверка прямолинейности
- •1.4.4.3. Выверка соосности
- •1.4.4.4. Выверка горизонтальности
- •1.4.4.5. Выверка вертикальности
- •1.4.4.6. Выверка наклона
- •Установка
- •Геодезический контроль монтажа, съемка и рихтовка подкрановых путей
- •1.5.3. Основные причины деформаций
- •Осадочные марки
- •1.5.6.Линейно-угловые построения для наблюдения за деформациями
- •1.5.6.1. Виды специальных сетей и особенности их построения
- •1.5.6.2.3.Схемы створных измерений
- •1.5.7.Автоматизация наблюдений за деформациями зданий и сооружений
- •1.5.8.Особенности наблюдений за деформациями высотных зданий и сооружений
- •2. Линейные и гидротехнические объекты
- •2.1.1. Полевое трассирование
- •2.1.1.9. Разбивка поперечных профилей (строительных поперечников)
- •2.1.1. Геодезическое обеспечение проектирования и строительства автомобильных и железных дорог
- •2.1.3. Виражи на автомобильных дорогах
- •2.1.4. Серпантины
- •2.1.5. Разбивка примыканий и пересечений автомобильных дорог
- •2.1.6. Железные дороги
- •Строение земляного полотна железной дороги
- •2.1.7. Съемка железнодорожных путей
- •А) Способ эвольвентных разностей
- •2.1.8. Геодезические работы при гидротехнических изысканиях
- •Известно, что в нивелировании
- •После подстановки формулы (а) в (12) получим рабочую формулу
- •2.1.9. Топографо-геодезические работы на водохранилищах
- •В) Стереофотограмметрический метод
- •3.Подземные сооружения
- •3.1. Назначение и способы возведения подземных сооружений
- •3.2. Понятие о габарите и форме поперечных сечений
- •3.3. Назначение геодезических работ при проектировании и строительстве туннелей
- •4. Способы проектирования трассы тоннеля
- •Геометрический способ
- •Аналитический способ
- •3.4.1. Основные элементы трассы в плане и профиле
- •1) Расчет координат пикетов через центральные углы
- •2) Вычисление координат по стягивающим хордам
- •3.8.Расчет необходимой точности измерений
- •3.8.1.Туннельная триангуляция
- •3.8.3. Точность ориентирования подземной основы
- •3.8.4. Точность подземной полигонометрии
- •3.8.5. Точность высотного обоснования
- •3.9.1.2. Способ створа двух отвесов
- •3.9.1.4. Способ шкалового примыкания к отвесам
- •3.9.1.5. Способ оптического клина
- •3.9.1.6. Способ поляризации светового потока
- •3.9.1.7.Автоколлимационный способ
- •3.9.1.8. Гироскопическое ориентирование
- •3.9.1.10. Ориентирование способом соединительного треугольника
- •3.9.1.10.1. Геометрическая схема ориентирования
- •3.9.1.10.2.Оптимальная форма соединительного треугольника
- •3.9.1.10.5. Косвенный способ примыкания к отвесам в подземной выработке
- •3.9.1.10.6.Уравнивание соединительного треугольника
- •3.11. Геометрическое нивелирование в подземных выработках
- •3.13. Закрепление знаков подземной полигонометрии
- •3.13. Измерения в подземной полигонометрии .
- •2) Измерения углов
- •3.14. Измерения в подземной полигонометрии
- •2) Измерения углов
- •3.15. Вынесение оси трассы в натуру
- •3.16.3. Определение опережения и укладка колец на кривых
- •3.16.4.Определение правильности положения колец в плане и в профиле
- •3.17.Геодезические работы при укладке железнодорожных путей в тоннеле
1.3.2. Способы разбивочных работ
1.3.2.1. Способ полярных координат
Для перенесения в натуру проектной точки P строят в опорном пункте A полярный угол , откладывают расстояние S и фиксируют точку (рис. 87).
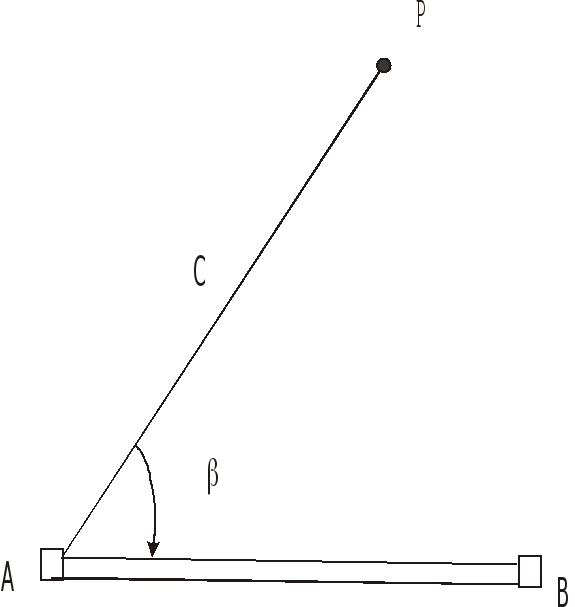
Рисунок 87 - Способ полярных координат
Точность разбивки этой точки без учета погрешностей исходных данных определяют по формуле:
![]() ,
,
где ms- средняя квадратическая погрешность отложения расстояния S;
m- средняя квадратическая погрешность построения угла;
me,me1- средние квадратические смещения разбиваемой точки, обусловленные соответственно неточностью центрирования теодолита и визирной марки на исходной стороне;
mф- средняя квадратическая погрешность фиксации разбиваемой точки.
При условии равного влияния погрешностей угловых и линейных измерений имеем:
![]()
![]()
![]() ;
;![]() .
.
1.3.2.2. Способ створно-линейных координат
Этот способ применяют в случае, если разбиваемая точка находится на опорной линии между ее концами или на ее продолжении. Теодолит и визирную цель размещают на концах опорной линии и по направлению визирования трубой теодолита откладывают проектное расстояние S и фиксируют точку C (рис. 88,а). Погрешность разбивки точки определяют по формуле:
![]() ;
;![]()
где mств- погрешность створа;
mS- погрешность построения длиныS;
mф- погрешность фиксации точки;
mu- СКО исходных пунктов;
mвиз- СКО фокусирования (визирования).
а) разбиваемая точка на опорной линии

Рисунок 88 – Способ створно-линейных координат
Если разбиваемая точка находится на продолжении опорной линии (рис. 88,б), то створ задается либо поворотом трубы через зенит, либо построением угла в 180(в обоих случаях при двух положениях круга и аналогично полярному способу). Более производительный и точный первый способ.
б) точка вне опорной линии.
Если точку P разбивают на продолжении створа AB, то погрешность построения самого створа возрастает пропорционально его длине, поэтому применять этот способ на большом протяжении не рекомендуется.
Пример. Требуется разбить точку P в створе линии строительной сетки длиной 200 м, имеющей предельную относительную погрешность 1: 10 000, на расстоянии 75 м при помощи теодолита типа Т-2 в комплекте с визирными марками, снабженными оптическими центрирами (линейные элементы центрировки и редукции e = e1 = 0.5 мм ), и мерного прибора, обеспечивающего измерение линии с погрешностью mS= 5мм.
В результате расчета получено:
![]() me=0,2
мм;
me=0,2
мм;
![]() ;me1=0,1
мм;
;me1=0,1
мм;
![]() ;
;
![]()
где b- длина створа;
30- средняя разрешающая способность невооруженного глаза;
v- увеличение зрительной трубы.
При фиксации точки с погрешностью mф= 0.5 мм получим:
![]() мм.
мм.
Здесь влияние отложения длины оказалось доминирующим.
1.3.2.3. Способ прямоугольных координат
В основу способа положена разбивка проектной точки P от линии геодезической основы AB, чаще - от линии строительной сетки, полигонометрии или теодолитного хода (рис. 89) по прямоугольным координатам x и y относительно точки A, взятой за начало частной системы координат, и линии AB - в качестве частной оси абсцисс.
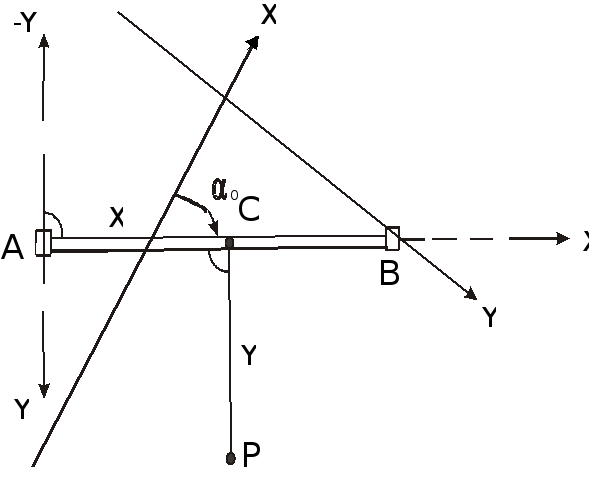
Рисунок 89 - Разбивка точки способом прямоугольных координат
Прямоугольные координаты определяют по формулам:
![]()
где XA, XP, YA,YP- абсолютные координаты исходной и проектной точек;
0- дирекционный угол опорной линии AB.
Знаки ординат указывают направление откладывания их от створных точек линии AB: при положительной - вправо, при отрицательной - влево. Если абсцисса x отрицательная, то ее откладывают от точки A в противоположном направлении линии AB.
Для разбивки точки теодолит устанавливают в пункте А и ориентируют по линии AB при помощи визирной цели, установленной в пункте B. Затем вдоль линии визирования откладывают расстояние x и фиксируют створную точку C. Устанавливают в ней теодолит, строят прямой угол при двух положениях круга с выбором средней точки и, отложив ординату y , фиксируют проектную точку P.
Среднюю квадратическую погрешность точки P определяют по формуле:
![]()
Здесь в скобки заключены погрешности установок и фиксации, влияние которых невелико. Поэтому, применив к отдельным членам подкоренного выражения принцип комбинированного влияния (равного и неравного в зависимости от величины составляющих), получим:
![]()
![]()
![]()
![]()
где T - знаменатель предельной относительной погрешности линейных измерений при откладывании расстояний;
m - некоторая вспомогательная погрешность;
v- коэффициент соотношения погрешностей, принимаемый в зависимости от имеющихся инструментов и условий производства работ (обычноv= 2, 2.5 или 3).
Пример. Определить, с какой погрешностью следует производить разбивку проектной точки с прямоугольными координатами x = 80 м и y = 60 м, если ее среднее квадратическое отклонение от проекта не должно превышать mр= 25 мм.
Приняв v= 2, получим T3 000; m< 57; me= me1= mф= 3.4 мм. По этим данным выбирают приборы для производства работ: теодолит 30точности, рулетку, тонкую веха. Приборы центрируют средним нитяным отвесом, точки фиксируют шпилькой на колышке.
1.3.2.4. Способ полярно- прямоугольных координат
Этот способ является модификацией способа прямоугольных координат с той лишь разницей, что координаты строят на вспомогательной линии AB', составляющей угол с линией геодезической основы AB.
Например, по условиям строительства необходимо разбить ряд точек P1, P2, ..., Pn, находящихся на одной прямой или нескольких параллельных прямых с заданным дирекционным углом(рис. 90). При известных дирекционных углахи0направлений AB и AB' определяют угол=-0. Откладывая его от направления AB, строят вспомогательную линию AB'. Она является базовой для построения прямоугольных координат x и y пунктов застройки, найденных по формулам:
![]()
с использованием дирекционного угла a линии AB'.
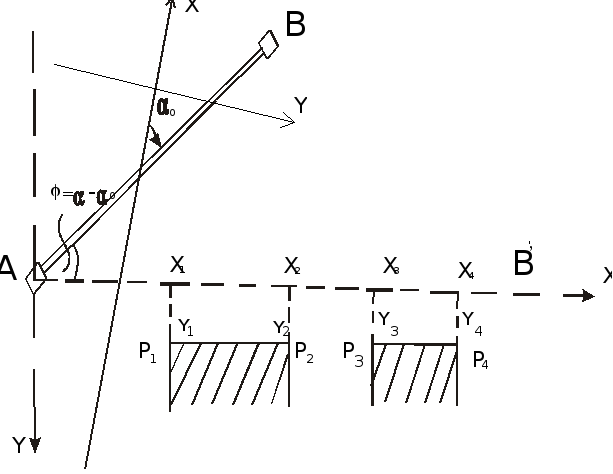
Рисунок 90 - Способ полярно-прямоугольных координат
Применение способа полярно-прямоугольных координат позволяет сократить длины ординат и создать лучшие условия для разбивочных работ. Точность разбивки определяют по формуле:
![]()
с учетом погрешности разворота линии АВ, выраженной зависимостью:
![]()
где m- погрешность построения угла.
1.3.2.5. Способ прямой угловой засечки
Этот способ применяется для разбивки удаленных и труднодоступных объектов - мостовых переходов и гидротехнических сооружений. При этом, положение проектной точки P с известными координатами определяют в натуре путем построения двух проектных углов 1и2соответственно в двух твердых пунктах A и B (рис. 91).
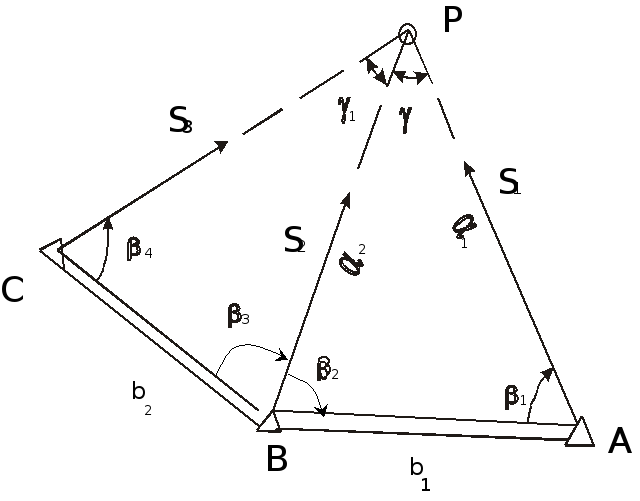
Рисунок 91 - Прямая угловая засечка
На точность разбивки влияют следующие источники: погрешность собственно прямой засечки и погрешность, обусловленная неточностью фиксации линий засечки (более подробно рассмотрено в вопросе мостовой триангуляции).
1.3.2.6. Способ замкнутого треугольника
Способ используется для уточнения положения точки, разбиваемой прямой угловой засечкой, главным образом при отсутствии дополнительных опорных пунктов.
Теодолит устанавливают в найденной точке и измеряют третий угол треугольника. Распределив невязку поровну или в соответствии с весами измеренных углов, определяют координаты точки Р (рис. 92). Сравнив их с проектными, находят поправки - редукции, на которые смещают первоначально найденную точку в проектное положение.
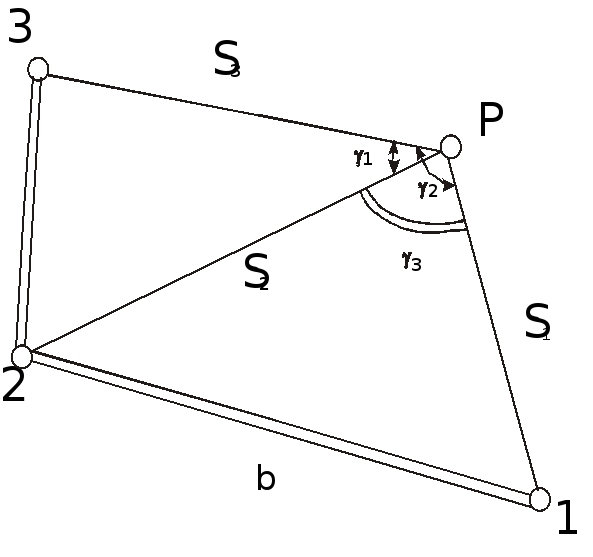
Рисунок 92 - Вставка точки в треугольник
Для оценки точности ее определения применяют формулу Ф. Красовского (без учета исходных данных).
![]()
При разбивке точки с трех пунктов (при вставке точки в треугольник) применяют формулу проф. К.Л. Проворова :

где
![]() - углы засечки соответственно между
визирными лучами 2 и 3, 1 и 3, 1 и 2;
- углы засечки соответственно между
визирными лучами 2 и 3, 1 и 3, 1 и 2;
![]() - длины визирных лучей с пунктов 1, 2, 3.
- длины визирных лучей с пунктов 1, 2, 3.
1.3.2.7. Способ линейной засечки
Способ применяется, в основном, для разбивки точек сооружений по расстояниям S1иS2, которые не превышают длины мерных приборов. Свето-, радио- и оптические дальномеры целесообразно применять по методу редуцирования. Разбивка состоит в нахождении точки пересечения дуг, построенных мерными приборами длинойS1иS2, поэтому ее можно осуществлять двумя или поочередно одним мерным прибором (рис. 93).

Рисунок 93 - Построение точки способом линейной засечки
Точность разбивки определяют по формуле:
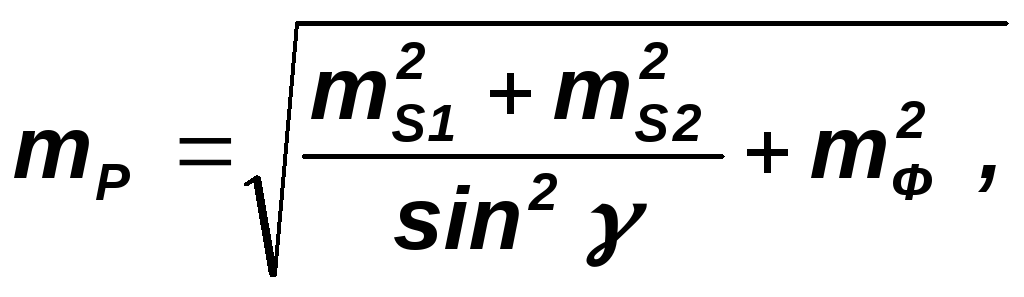
где
![]() - погрешности откладывания длинS1иS2;
- погрешности откладывания длинS1иS2;
![]() -
погрешность фиксации точки.
-
погрешность фиксации точки.
1.3.2.8. Способ створной засечки
Способ заключается в определении положения точки на пересечении двух створов, составляющих между собой угол засечки . Обычно, створы задают теодолитами, проволоками или струнами. Благодаря простоте применения и высокой точности, этот способ широко применяется в промышленном строительстве при пересечении створов под прямым углом (=90).
По характеру проявления погрешностей, способ близок к способу прямой угловой засечки, но точнее его. Погрешность разбивки точки способом створной засечки определяют по формуле:
![]()
где
![]() - погрешности построения створов.
- погрешности построения створов.
1.3.2.9. Способ обратной угловой засечки
Способ применяется для уточнения положения приближенной точки сооружений при помощи измеренных на ней горизонтальных углов 1,2,3на три опорные пункта (рис. 94) с последующим редуцированием (при разбивке центров мостовых опор, бычков плотин и других сооружений).
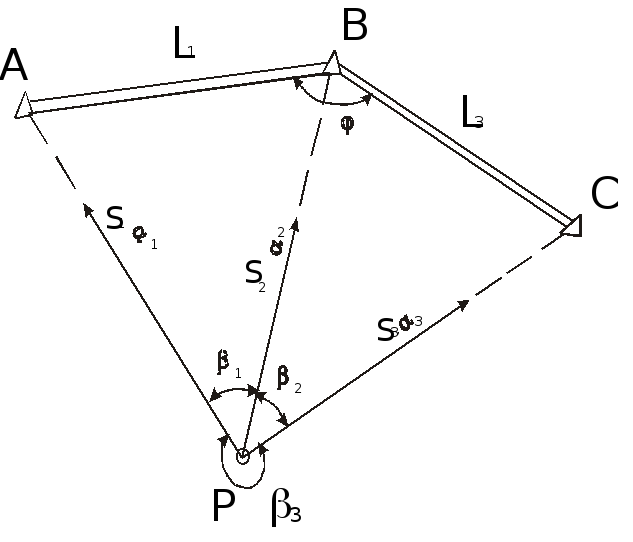
Рисунок 94 - Обратная засечка
Погрешность положения точки определяют по формулам:
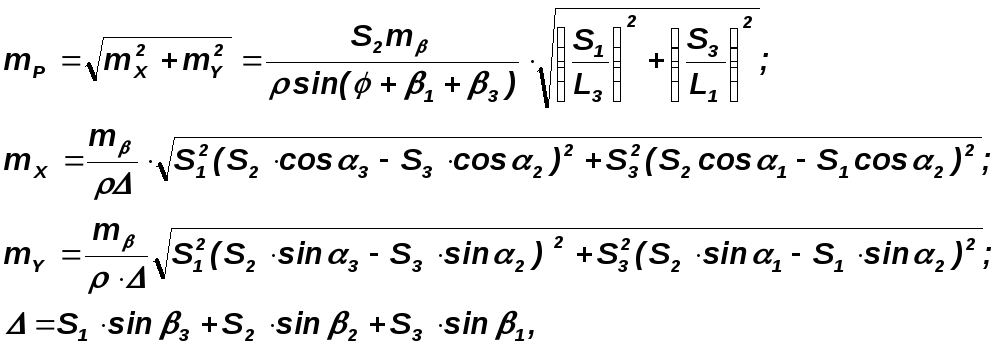
где
![]() - расстояния от опорных пунктов;
- расстояния от опорных пунктов;
![]() -
дирекционные углы направлений засечки;
-
дирекционные углы направлений засечки;
![]() - расстояния между опорными пунктами 1
и 2, 2 и В;
- расстояния между опорными пунктами 1
и 2, 2 и В;
![]() - угол на пункте В между сторонами опорной
сети.
- угол на пункте В между сторонами опорной
сети.
Общую редукцию (смещение точки Р в проектное положение Р0и ее ориентировку) определяют по разности абсцисс и ординат указанных точек. В связи с большим объемом вычислений при малых величинах смещений, целесообразно пользоваться дифференциальным методом.
Контроль определения осуществляется по четвертому опорному пункту. Необходимо помнить, что обратная засечка не имеет решения, если определяемая точка и все опорные точки находятся на проведенной через них окружности («опасная окружность»). По исследованиям, уход наружу и вовнутрь «опасной окружности» на расстояние 10% ее радиуса уже обеспечивает уверенное определение точки, так как сумма углов (2 +1 +3)180.
1.3.2.10. Способ проектного полигона
Способ применяется для разбивки вытянутых подземных и надземных сооружений - тоннелей, каналов, линий электропередачи (ЛЭП), трубопроводов, кабелей и т.п. Этот способ часто называют способом полигонометрии.
Сущность его заключается в последовательном применении полярного способа определения положения точек. Полигонометрический (теодолитный) ход исходит из пункта геодезической основы и включает в себя разбивочные точки сооружения (рис. 95).
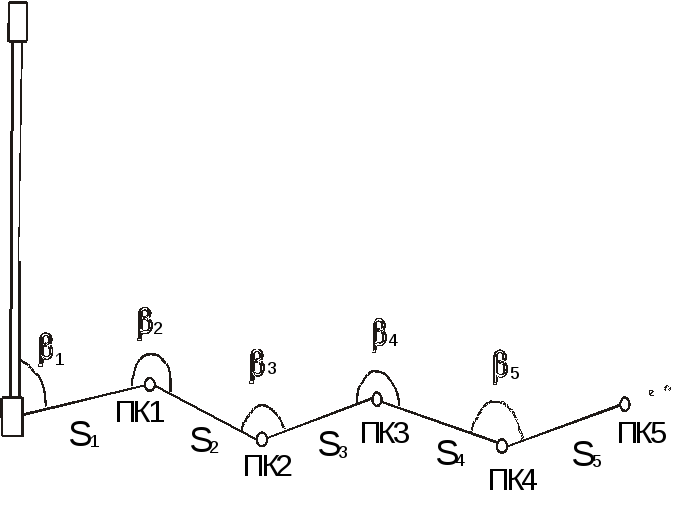
Рисунок 95 – Способ проектного полигона
Ходы могут быть висячими и разомкнутыми. Точность измерения углов и длин линий в ходах определяется требованиями к точности разбивки сооружений. Расчет точности ведется по соответствующим формулам полигонометрии. Уравнивание проектного полигона сводится к перемещению его пунктов параллельно невязке и пропорционально удалению искомого пункта от начального. Если местоположение сооружения неизвестно, то полигонометрический ход прокладывают вблизи оси сооружения. После уравнивания хода разбивают точки сооружений из пунктов полигонометрического хода, например, полярным способом. Иногда полигонометрический ход заменяют другими видами геодезической основы - триангуляцией, трилатерацией или линейно-угловой сетью.
1.3.2.11. Разбивка точек способом редуцирования
При точных и высокоточных разбивочных работах, однократное построение разбивочных элементов (углов и длин линий) не обеспечивает достаточной точности, поэтому, применяют метод редуцирования.
Метод редуцирования заключается в смещении приближенной точки в проектное положение.
Основные этапы метода включают:
предварительную разбивку приближенной точки
точное измерение элементов разбивки для приближенной точки
сравнивание их с проектными величинами и вычисление редукций (отклонений)
смещение приближенной точки в проектное положение на основании вычисленных величин редукций.
Значение редукций удобно представлять прямоугольными или полярными координатами, и привязывать их к одному из направлений визирования с опорного пункта, которое принимается в качестве условной оси абсцисс. Направление смещения приближенной точки в проектное положение определяется знаком прямоугольных редукций rx иry.По ним вычисляют угловой и линейный элементы общей редукции, привязанной к условной оси абсцисс по формулам:
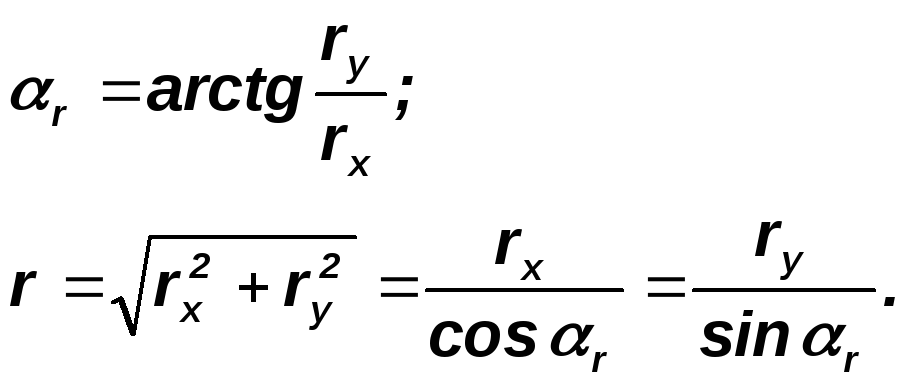
Способ реализации редукций зависит от их величины: при r200 мм применяется полярный способ с откладыванием угла теодолитом и расстояния- рулеткой. Приr< 100-200 мм - способ прямоугольных координат с использованием координатной палетки.
Палетка изготавливается из прозрачного синтетического материала, например лавсана, размером 200x200 или 400x400 мм с сеткой 10x10 мм (рис. 96).
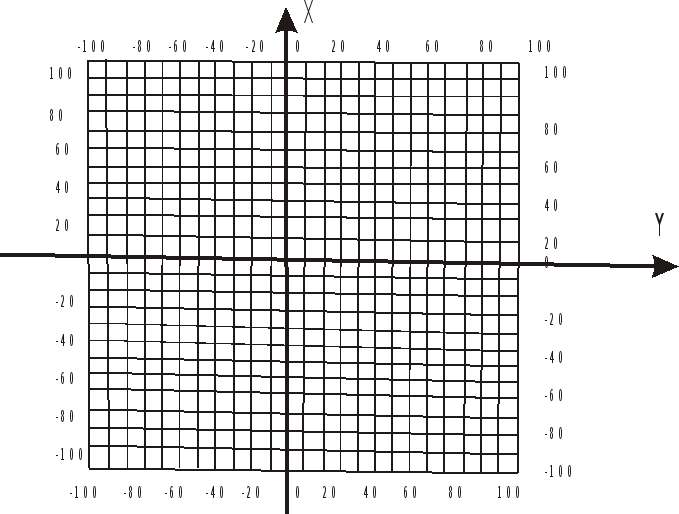
Рисунок 96 - Редукционная палетка
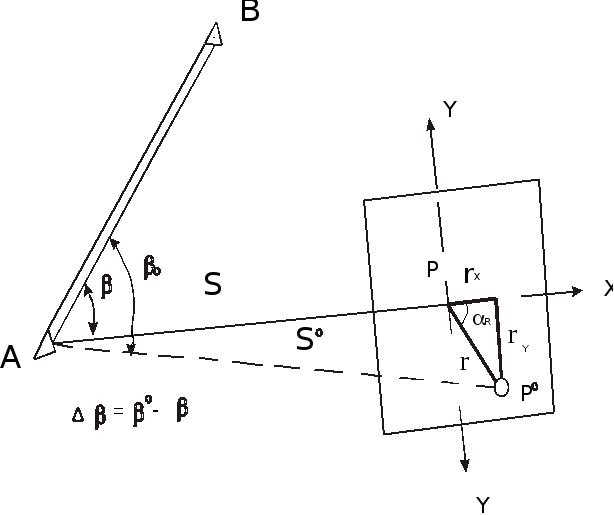
Рисунок 97 - Редуцирование точки при способе полярных координат
Для редуцирования палетка укладывается началом координат в приближенной точке и ориентируется по направлению условной оси абсцисс. Затем, на палетке откладывают величины редукций rxиryс учетом их знаков. Проектная точка фиксируется на сооружении - металлической пластине знака, бетона и т. п. Основной недостаток палетки, укладываемой на земле, - трудность ориентирования ее по условной оси абсцисс, что приводит к ее развороту и, как следствие - к погрешностям редуцирования. Поэтому, удобнее пользоваться специальным геодезическим редукционным прибором (ГРП), разработанным в Киевском инженерно-строительном институте.
Прибор (ГРП) представляет собой двух координатный измерительный столик с втулкой подставки в середине для размещения визирной марки, отражателя дальномера, оптического центрира или теодолита. При помощи трех становых винтов столик прикрепляют к рамной головке специального штатива. Координатные оси столика по линии визирования ориентируют при помощи оптического визира с поворотным зеркалом. Подставка, закрепляющая приближенную точку, смещается двумя штурвалами. При этом, величина перемещения измеряется на шкалах координатного столика. Проектная точка сносится на рабочий горизонт (выше или ниже столика) при помощи оптического центрира или прибора вертикально визирования.
Для способа полярных координат(рис. 97) редукции имеют вид:
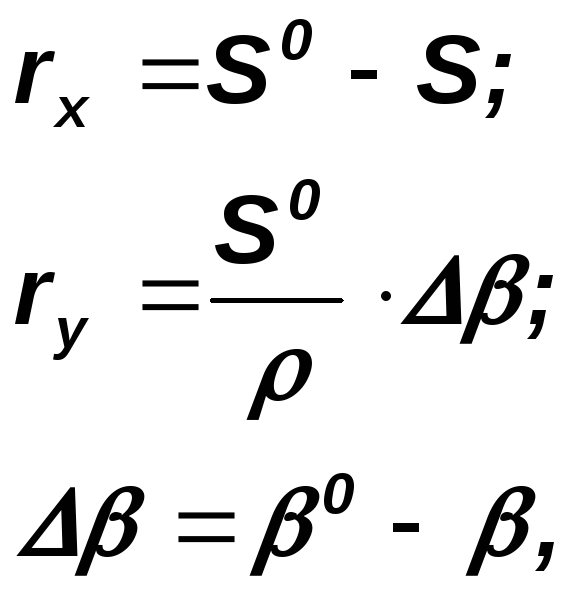
где
![]() - расстояния и горизонтальные углы к
проектной Р0и приближенной Р
точкам сооружения.
- расстояния и горизонтальные углы к
проектной Р0и приближенной Р
точкам сооружения.
Редукции rxиryпривязаны к точке Р и направлению АР, взятым условно за начало координат и положительное направление оси абсцисс.
Аналогично получается и в способе створно-линейных координат, однако здесь величинуryудобно свести к нулю перемещением подставки теодолита ГРП в поперечном направлении.
В способе прямоугольных координат, который является комбинацией способов створа и полярных координат, редуцирование рационально производить раздельно: сначала для створной, а затем - для конечной точки, аналогично полярному.
При разбивке точек сооружений 3-х лучевой прямой угловой засечкой, переносят в натуру приближенную точку Р (рис. 98), измеряют для нее углы1,2,3. Сопоставляя их с проектными значениями10,20,30 , вычисляют вспомогательные величины:

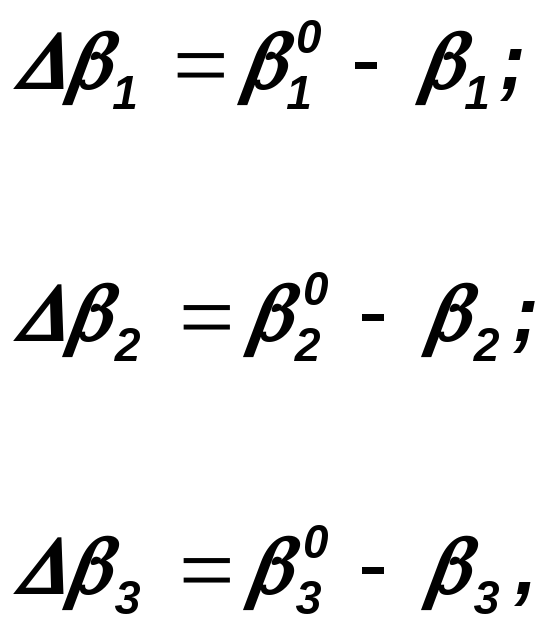
а затем и сами редукции:
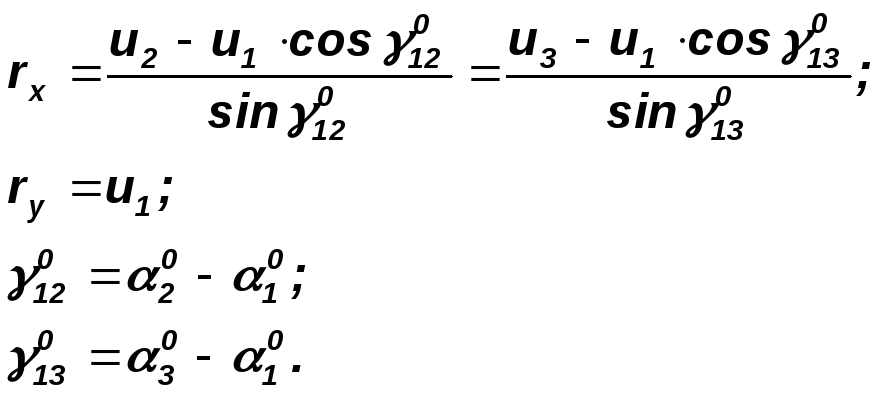
где
![]() - проектные расстояния и дирекционные
углы направлений засечек.
- проектные расстояния и дирекционные
углы направлений засечек.

Рисунок 98 - Редуцирование точки в способе угловой засечки
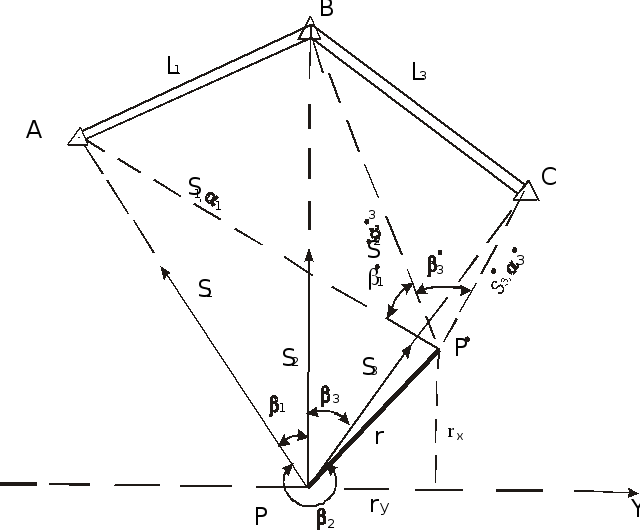
Рисунок 99 - Редуцирование точки при обратной угловой засечке
Аналогичное положение имеем при створной засечке. Так как в промышленном и гражданском строительстве сворная засечка применяется с =90, то:
Реализация таких редукций при помощи ГРП очень проста, эффективна и точна.
Для прямой линейной засечкис трех пунктов (см. рис. 98) определяют следующие величины:
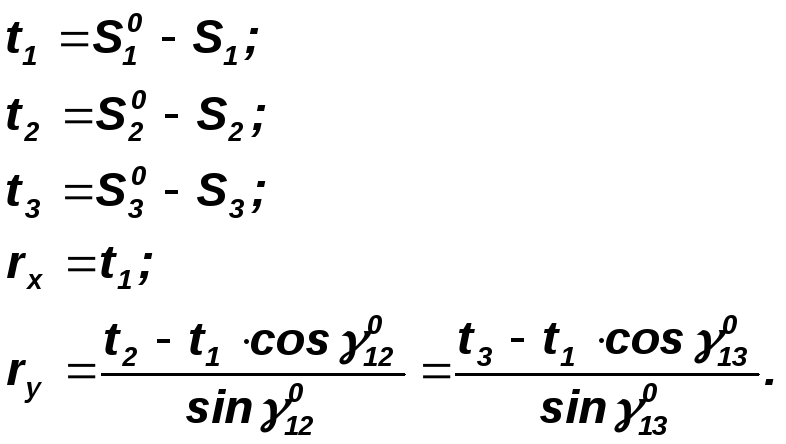
В обратной линейной засечке, когда исполнитель находится в разбиваемой точке, эти редукции меняют знак. Так, в случае однократной обратной угловой засечки (рис. 99) по разностям углов находят следующие величины:
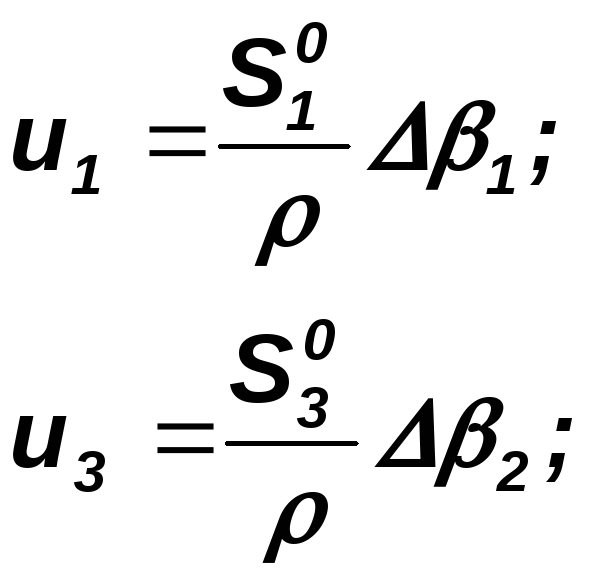
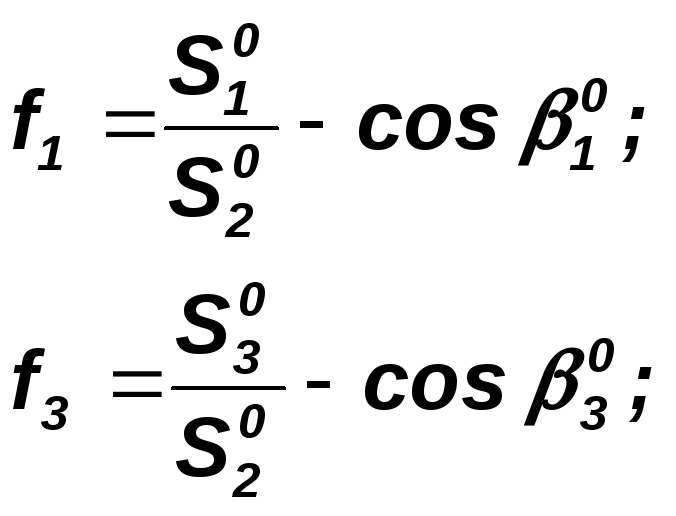
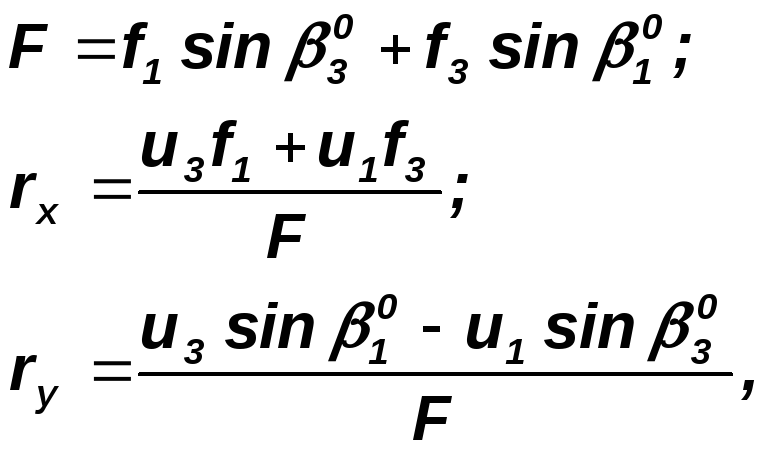
где
![]() - вспомогательные величины, которые
можно вычислить до начала полевых работ.
- вспомогательные величины, которые
можно вычислить до начала полевых работ.
Редукции привязаны к среднему направлению Р-В, принятому в качестве условной оси абсцисс. Если используется четвертый опорный пункт, решение сводится к двум задачам. По указанным величинам упрощается и оценка точности редукций:
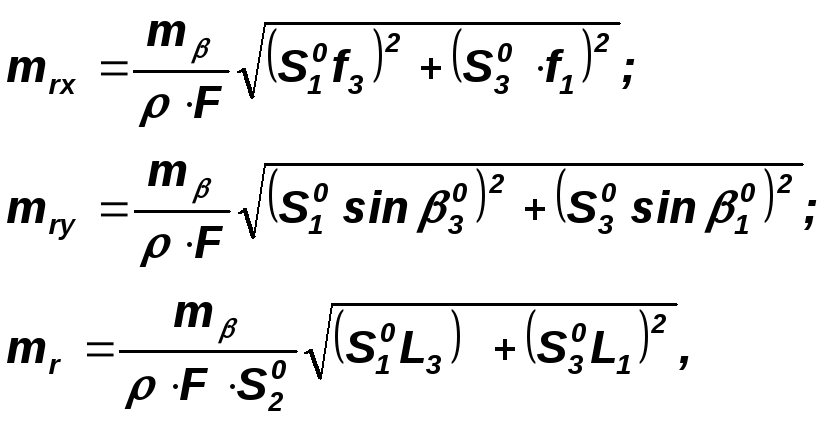
где
![]() - погрешность измерения угла;
- погрешность измерения угла;
![]() - длины твердых сторон 1-2 и 2-3.
- длины твердых сторон 1-2 и 2-3.
В способе обратной биполярной засечки, применяемой для введения приближенной точки С в створ линии АВ при отсутствии видимости между ее концами, определяют угол нестворности=180-, где- угол между направлениями на твердые пункты.
На рисунке 100 показано три случая решения задачи для смещения одной, двух и трех приближенных промежуточных точек С в створ при наличии взаимной видимости между ними и конечными пунктами створа. Необходимые редукции вычисляют по формулам:
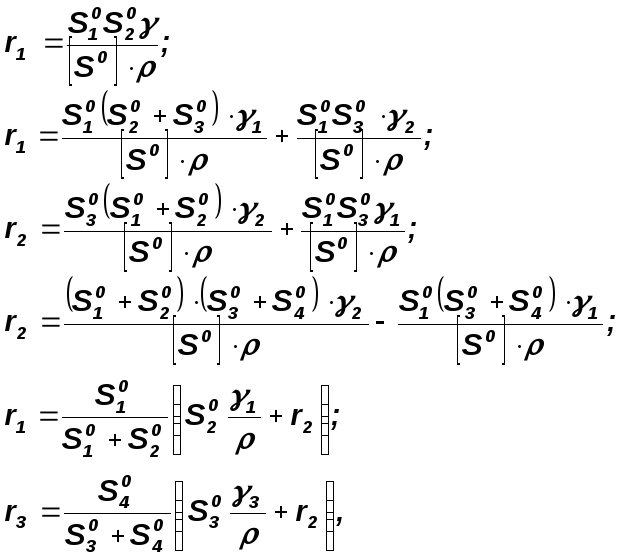
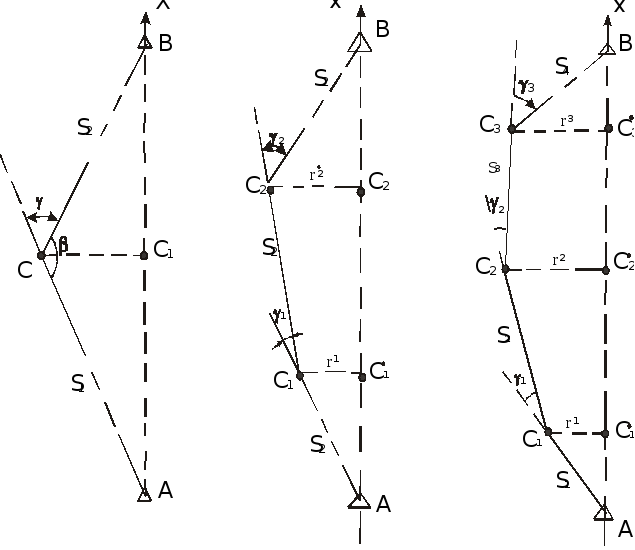
Рисунок 100 - Способ обратных биполярных засечек
где r- редукции - перпендикуляры к направлению створа; [S0] - длина створа АВ.
Точность определения редукций зависит от степени приближения точки С к створу: чем ближе точка к створу, тем выше точность. Погрешность редукций выражается приближенной зависимостью:
![]()
где S- средняя длина луча визирования;
n- число промежуточных точек свора;
i- порядковый номер промежуточной точки в створе относительно его конечных пунктов;
![]() - погрешность измерения угла
нестворности.
- погрешность измерения угла
нестворности.
Данный способ применяется при разбивке осей сооружений (определение точки их пересечения), трассировании ЛЭП, канатных дорог и т.п. Редукцию при всех способах разбивки вычисляют по простым формулам, без высокой точности (на счетной линейке). Вспомогательные величины (углы, дирекционные углы и расстояния) можно получить графически с плана с относительной погрешностью 1: 300. Высокая точность измерений требуется только для основных элементов, определяющих точность разбивки точек сооружений.
При избыточных измерениях определяют средневзвешенное (редко - среднее) значение редукций. В сложных системах рационально определять редукции из уравнивания измеренных величин, например, параметрическим методом.
