1.1.4.3. Способы детальной разбивки строительной сетки

От вынесенного и закрепленного в натуре исходного направления и выполняют разбивку всей строительной сетки. Для этого используют один из двух основных способов: осевой способ и способ редуцирования

1.1.4.3.1. Осевой способ

При осевом способе (иногда его называют способом точного построения элементов) сетку сразу строят на местности с расчетной точностью путем точного отложения проектных элементов. Найденные точки тут же закрепляют постоянными знаками. Выполнив затем между центрами этих знаков точные угловые и линейные измерения, определяют их фактические координаты. Вследствие накопления ошибок они могут оказаться не кратными длинам сторон сетки. С целью корректирования к головке знака приваривают стальную пластинку 10х10 или 15х15 см. Однако и в этом случае, при больших размерах площадки, даже сдвинув центр к краю пластинки, можно не добиться получения проектных координат, что сведет на нет все достоинства строительной сетки. Поэтому применение осевого способа ограничено. В то же время он обладает тем достоинством, что все пункты сетки сразу же закрепляются постоянными знаками. Рассмотрим технику применения этого способа.

При разбивке строительной сетки этим способом стремятся вынести два взаимно перпендикулярных начальных направления АВ и АС, пересекающихся примерно в середине площадки (рис.39).

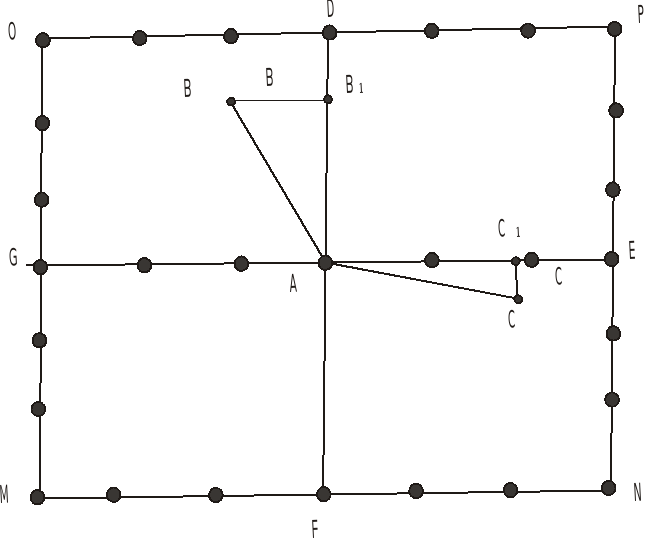
Рисунок 39 - Разбивка строительной сетки осевым способом

Поскольку точки А, В и С выносят на основании графических данных, угол ВАС может значительно отличаться от прямого. Его измеряют 2 - 3 приемами теодолитом типа Т2 и определяют отклонение от прямого:

 = 90 - ,

где  - измеренное значение угла.

После этого вычисляют поправки в положение точек В и С:

; ,

причем расстояния S_AB и S_AC достаточно знать с точностью до метра. Сместив точки В и С на вычисленные поправки, получают две взаимно перпендикулярные оси АВ и АС (отсюда и название способа). Вдоль этих осей откладывают в створе по теодолиту отрезки, равные принятым длинам сторон сетки.

Измерения выполняют точными приборами с учетом всех поправок (метеоусловия, компарирование, наклон). Для этой цели можно использовать компарированные ленты с измерением по кольям или точные оптически дальномеры. Весьма эффективны электронные тахеометры, снабженные микропроцессорами, позволяющие быстро вычислять горизонтальные проложения с учетом всех поправок. Закончив разбивку по осям в точках D, Е, F и G, строят на них прямые углы и продолжают разбивку по периметру сетки. Вследствие накопления ошибок на стыках линий периметра в точках М, N, О и Р будут образовываться невязки. Их величины характеризуют точность работ. Для ослабления ошибок разбивки перемещают несколько точек, ближайших к угловым. После этого временные знаки по всеми периметру заменяют постоянными. Затем, по створам между соответствующими точками периметра и осей разбивают и закрепляют все внутренние точки в полигонах АDPЕ, АЕNF, АFМG и AGOD.

Для определения окончательных координат выполняют точные измерения, для чего прокладывают полигонометрические ходы, либо используют другие методы.

Применение осевого способа имеет смысл на небольших площадках или там, где точность разбивочных работ невелика и отступлением координат пунктов от проектных значений в пределах 3 - 5 см можно пренебрегать.

Для проектирования и выполнения разбивочных работ удобнее иметь такую сетку, координаты пунктов которой практически не отличаются от проектных, чего можно достичь при построении ее способом редуцирования.

Поскольку способ редуцирования получил наиболее широкое распространение при разбивке строительных сеток вообще, а на больших промышленных площадках исключительно он и используется, дальнейшее рассмотрение строительных сеток в основном на него и ориентировано, хотя основные схемы построения и математической обработки сетей могут быть использованы и при применении осевого способа.