1.1.4.9. Методы построения сетей второго порядка

1.1.4.9.1.Полигонометрия

Полигонометрию 2-го порядка строят в виде вытянутых ходов (в случае сетки из одинаковых прямоугольников или квадратов - с равными сторонами), опирающихся на пункты полигонометрии 1-го порядка и прокладываемых по кратчайшему расстоянию между ними. Недостатком полигонометрии является отсутствие взаимной связи между соседними ходами. Поэтому, учитывая важность обеспечения достаточной точности взаимного положения соседних пунктов, следует несколько завышать точность измерений по сравнению с получаемой из расчетов на допуски разбивочных работ и исполнительных съемок. Это относится и к любым другим методам, при применении которых пункты внутри каркаса получают из отдельных взаимно не связанных построений.

Исходя из полученной средней квадратической ошибки 4.1 см положения пункта, находящегося в середине хода 2-го порядка, получим средний линейный сдвиг в конце хода 9 см, и предельно допустимую абсолютную невязку хода  18 см. При длине хода 1 - 1,5 км это приведет к предельной относительной невязке хода 1: 6 000 - 1: 10 00. Учитывая сказанное выше, не следует прокладывать ходы 2-го порядка с предельной относительной ошибкой более 1: 10 000.

Поскольку сети 2-го порядка служат для определения координат основной массы пунктов строительной сетки, при построении которой одинаково нежелательны деформации как в продольном, так и в поперечном направлении, расчет необходимой точности измерений в полигонометрии выполняют, исходя из принципа равных влияний продольных и поперечных ошибок, т. е. полагая, что ошибка положения пункта равна:

M² = m_t² +m_u² ,

где m_t , m_u - соответственно продольная и поперечная ошибки.

Следует принять:

m_t = m_u =M.

Сдвиг конечной точки вытянутого хода вычисляют по формулам:

; .

Средняя квадратическая ошибка в определении положения пункта в середине вытянутого хода полигонометрии между пунктами каркасной полигонометрии, равна:

m_c = M/2≤ 4.1 мм,

где M- ошибка положения пункта в конце хода , она вычисляется для хода АВ по формулам:

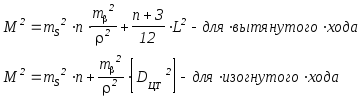
где n -число сторон хода;

[D_ЦТ²] - сумма квадратов расстояний от центра тяжести до текущих точек.

Средняя квадратическая ошибка взаимного положения пунктов CD (рис.48):

B

C D

A

Рисунок 48.

1.1.4.9.2. Метод четырехугольников без диагоналей

Сети четырехугольников без диагоналей, заполняя каркас, создают сплошную сеть (рис.49). Все пункты этой сети взаимно связаны и своей формой эта сеть напоминает строительную сетку. Так как диагональные направления не измеряются, то этот метод с успехом используется на застроенных и залесенных площадках.

Рисунок 49 – Схема построения четырехугольников без диагоналей

При расчете точности измерений в сети, уравненной между пунктами каркаса, можно использовать таблицу 7.

Таблица 7

Система построения Sx = Sy	Q	QSx	Qx	QSy	Qy
3x3 3x4 3x5 4x3 4x4 4x5 5x3 5x4 5x5	0,59 0,67 0,71 0,76 0,67 0,81 0,71 0,81 0,86	0,60 0,76 0,84 0,59 0,76 0,84 0,59 0,77 0,86	0,41 0,41 0,41 0,44 0,45 0,45 0,46 0,47 0,47	0,59 0,59 0,59 0,72 0,76 0,77 0,84 0,84 0,86	0,41 0,44 0,46 0,41 0,45 0,47 0,41 0,45 0,47

Нормированные обратные веса вычислены для наиболее слабых элементов сети, независимо от конкретной длины ее сторон. При этом приняты следующие обозначения:

Q -корень из нормированного обратного веса положения пункта в самом слабом месте сети;

Q_Sx , Q_Sy - то же - для длин соответствующих сторон;

Q_x , Q_y - то же - для дирекционных углов этих сторон.

Переход к сети с конкретными длинами сторон осуществляется по формулам:

; ;

; ;

где m_S2 и m_2 - требуемая точность длин сторон и дирекционных углов этих сторон.

В заполняющих сетях m_S=10 мм, m_=10.

Из этих четырех значений выбирают минимальное и вычисляют ошибку положения пункта:

M_II =K₁ m_(min) Q, K₁ =S/";

где S - длина стороны строительной сетки в мм.