II. Стереографические проекции.

N

A₁

A

O

A₂

Q

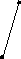
Для их построения действуют аналогично сферическим координатам. Есть точка, описываем ее сферой произвольного радиуса. Через центр сферы проводят плоскость Q-плоскость проекции. В результате пересечения плоскости со сферой имеем большой круг проекции.

S – «точка зрения»

Направление ОА продляем до пересечения со сферой. Затем соединяем А₁с «точкой зрения». Точка А₂ –стереографическая проекция направления ОА.

SA₁– луч зрения

Если направление под лучом к плоскости проекции, то это будет точка внутри круга проекции. Если направление перпендикулярно плоскости проекции, это точка в центре круга проекции (т. О). Если же направление параллельно плоскости проекции, то это две точки на круге проекции.

под углом к плоскости перпендикулярно параллельно плоскости

проекции плоскости проекции проекции

На стереографических проекциях оси симметрии обозначаются следующим образом:

L₂

L₃

L₄

L₆

Плоскость проекции обозначается (Р):

Центр проекции (С): С

Обозначение плоскостей:

Если плоскость параллельна основному кругу проекции.

Плоскость перпендикулярна плоскости проекции.

Дуга, если плоскость расположена под углом.

Рассмотрим обозначение осей, плоскостей симметрии на примере КУБА

Пример.

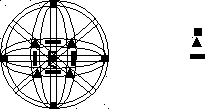
L₄(001)

В кубе: 3L₄-

4L₃-

6L₂-

Ш. Гномостереографические проекции.

Берется кристалл, строится его полярный комплекс и этот комплекс проецируется на плоскость проекции.

За центр тяжести многогранника принимается цент сферы (произвольного радиуса). Через точку О приводим горизонтальную плоскость Q и все условимся обозначать на этой плоскости.

N

n

b a a=a₁

b=b₁

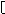
Qb₁c a₁dd₁d=d₁

m

 c d₁

S b₁a₁

Горизонтальные грани проецируются в центр круга проекций. Вертикальные (d₁) находятся на самом круге проекций. Косые грани внутри круга проекций.

IV. Гномонические проекции.

(используется в ренгено-структуром анализе)

Плоскостью проекции является ка-

сательная к северному полюсу.

Гномонические проекции плос-

костей – точка.

Гномоническая проекция направле-

ния – прямая.

Недостаток:При построении проекций не сохраняются угловые соотношения, но координаты точек на гномонической проекции прямо пропорциональны индексам Миллера.

Лекция 6 Решетки Бравэ

В 1848 году О.Бравэ вывел 14 типов решеток Бравэ.

Условия выбора элементарного параллелепипеда повторяемости.

1. Сингония выбранного параллелепипеда повторяемости должна соответствовать сингонии всей решетки.

2. Число равных ребер и углов между ребрами параллелепипедов должно быть максимальным.

3. При наличии прямых углов между ребрами параллелепипеда их число должно быть максимальным.

4. При соблюдении первых трех условий объем параллелепипеда должен быть наименьшим.

Ребра параллелепипеда повторяемости совпадают с элементарными трансляциями в решетке.