Лекция 2

Симметрия кристаллов

Учение о симметрии развивали в XIX веке Гадолин и Федоров.

Преобразования в пространстве, в процессе которых проявляется симметрия,называются симметрическими операциями.

Элементами симметрии называются вспомогательные геометрические образы (точки, прямые, плоскости), с помощью которых обнаруживается симметрия фигур.

Существует 5 видов симметрических операций.

1. Отражение

2. Вращение

3. Инверсия

4. Совокупность вращение (вращение-отражение)

5. Совокупность инверсия-вращение (вращение-инверсия)

В последних двух пунктах порядок не важен.

Отражение

Э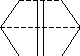лемент симметрии —плоскость симметрии.

А А₁ В учебной символике она обозначается

буквой Р, в международной — , на ри

В В₁ сунке — двумя линиями.

Плоскостью симметрии называется

такая плоскость, которая делит фигуру

С С₁ на 2 зеркально равные части, расположе

Р () нные друг относительно друга как пред

Рис.1 мет и его зеркальное отражение.(рис.1)

Практические указания

1. Плоскости симметрии проходят через середины граней и ребер, перпендикулярно им, или же идут вдоль ребер, образуя равные углы с одинаковыми гранями и ребрами.

2. При подсчете количества плоскостей симметрии в кристалле его надо держать в одном положении, чтобы не посчитать одни и те же плоскости несколько раз.

П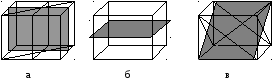ример

Гексаэдр.

рис.2

У гексаэдра 9 плоскостей симметрии, из которых 6 диагональных и 3, которые проходят через середины граней и ребер, перпендикулярно им. На рис.2.а показаны 4 грани, 2 из них диагональные; на рис.2.б — одна, на рис.2.в. — 4 диагональных.

Вращение

Элемент симметрии — линия, ось вращения.

Ось симметрии — прямая линия, вокруг которой несколько раз повторяются равные части кристалла.

Теорема

Элементарный угол поворота любой оси симметрии содержится целое число раз в 360⁰.

=360⁰

n , где n — порядок оси.

n=1, =360⁰ (это ось первого порядка, присутствует всегда)

n=2, =180⁰

n=3, =120⁰

n=4, =90⁰

n=6, =60⁰

L₁, L_2, L_3, L_4, L₆ — порядки осей в учебной символике.

1,2,3,4,6 — в международной символике.

В кристаллах нет осей симметрии пятого порядка, поскольку кристалл нельзя упаковать с помощью правильных пятиугольников.

Инверсия

Элемент симметрии — точка.

Центр инверсии — особая точка внутри кристалла, характеризуемая тем, что любая проведенная через нее прямая по обе стороны от нее и на равных расстояниях встречает одинаковые (соответственные) части кристалла.

Практическое указание

П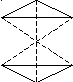ри наличии центра симметрии каждой грани отвечает другая грань, равная и параллельная первой (рис.3)

В

А Д

С

Д₁ А₁

В₁

Рис.3